4.28 二分搜索

三种二分搜索
框架：

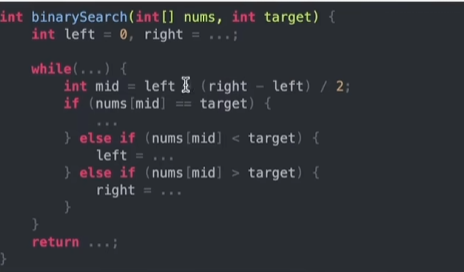
技巧1：代码不要出现else 而是用 else if取代（便于体现多种情况）
技巧2：mid计算方法：right+（left-right）/2
技巧3：while循环条件，是left<=right，如果是小于，则会出现（left=2，right=2）(会漏掉某一个元素)无法继续进行判断的情况（开始定义的区间是[0,nums.length-1]是一个左闭右闭的区间）
技巧4：更新left/right的时候，要更新成mid+1/-1（因为是闭区间）

1.寻找一个数（每个数只存在一个）
缺陷：如果有很多同样的值，不能返回一个确定的边界

2.寻找一个左侧边界
注意点1：left=0，right=nums.length-1，左闭右开区间
注意点2：while（left<right）当left=right的时候就结束（原因：左闭右开）最后的搜索区间有一个，但因为是左闭右开，所以实际上为空
注意点3：更新left=mid+1,right=mid
注意点4：if mid==target，right=mid
最后返回left（最后left和right是一样的）（小于目标值的元素有几个）

总结：（都写成左闭右闭的形式）
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}

int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回，锁定左侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
if (left < 0 || left >= nums.length) {
return -1;
}
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}

int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回，锁定右侧边界
left = mid + 1;
}
}
// 由于 while 的结束条件是 right == left - 1，且现在在求右边界
// 所以用 right 替代 left - 1 更好记
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}

几种二分的逻辑