4.8 偏序关系

回顾
等价关系：R（二元关系）是自反的，对称的和传递的
3可以整除6（注意写法）

1.1 相容关系
R是自反的，对称的，则称R是相容关系
相容类：取A的一个子集C，使得C里面容易两个元素都有相容关系，则称C为相容类
最大相容类，完全覆盖：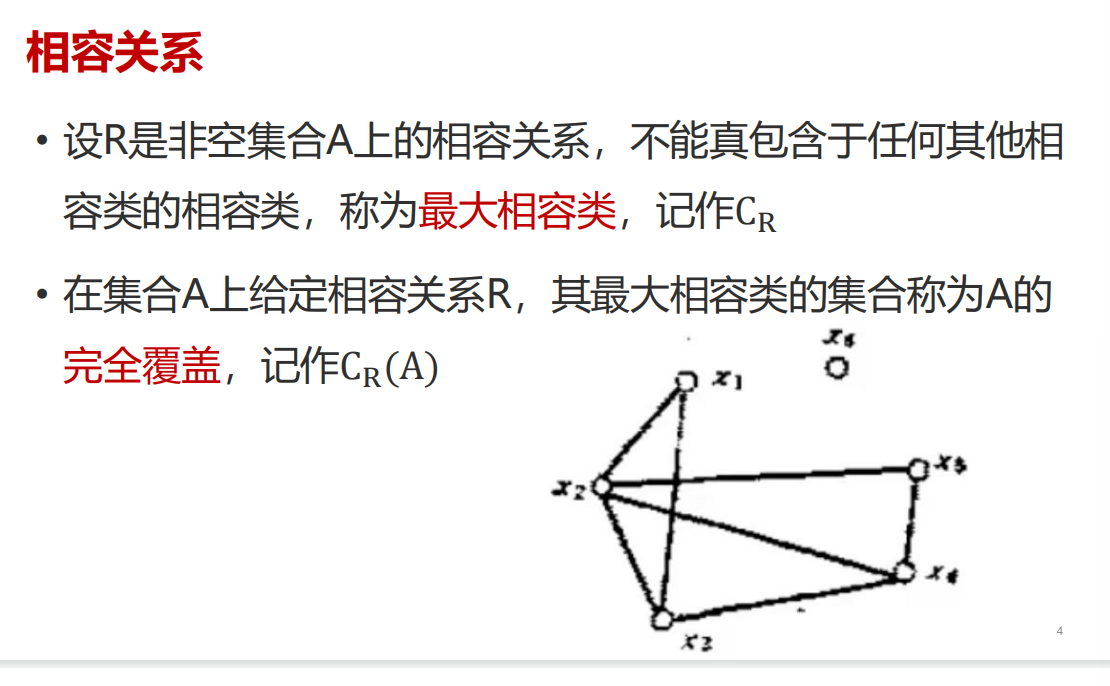
图中最大相容类是x1,x2,x3/x2,x3,x4
完全覆盖：{(x1,x2,x3),(x2,x3,x4)}
x1和x4,x5没有关系R

1.2 次序关系（现实中的一些事件必须在某些事物发生之后方可发生，也就是事物之间存在先后关系，即次序关系）
R是自反（a,a）满足这个关系，反对称若（x,y）,(y,x)都满足，则x=y，传递*若(a,b)(b,c)都满足关系，则必然有(a,c)，则称R是A上的偏序关系，记作≤（略有区别）
a≤b，读作a对b有偏序关系
集合A与偏序R一起称为偏序集，记作（A,R）

常见的偏序关系

偏序集中的元素间的可比性

如果元素满足偏序关系，就称两个元素可比，可比才能排序

积偏序

字典顺序

同构偏序
假设一个集合A,A'是偏序集，f:A->A'(是一个双射)，则称函数f是从(A,≤)到(A',≤)的一个同构

**偏序集的哈斯图（偏序关系的关系图）
盖住关系：

需要注意的点：

哈斯图的特点

可以先找到每个元素的父元素，然后再画

关系图改造成哈斯图

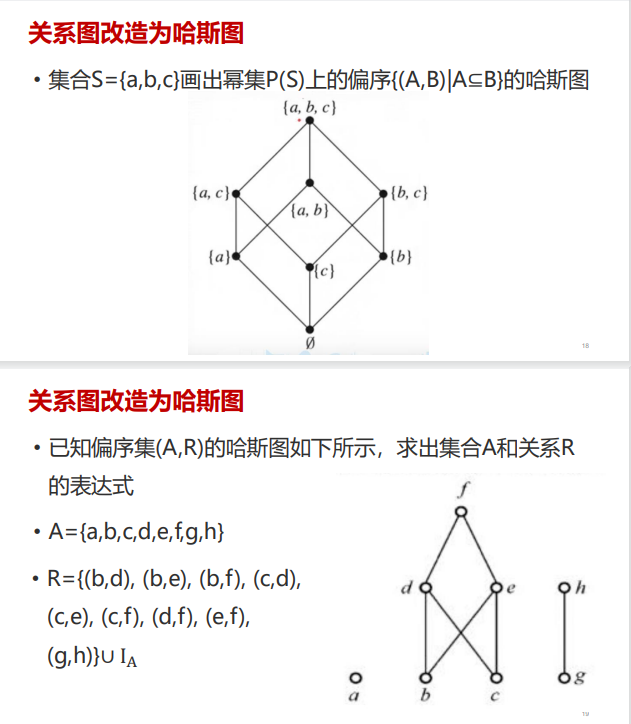
第一张图(a,b）也可以看作并没有写在c的上面，只是这样安排的位置
第二张图注意传递性！（在图上不会直接显示）

最大（小）元和极大（小）元

最小元：空集；最大元{a,b,c};
极小元（有并列小的）；极大元同理

可比：两个元素间有偏序关系

画哈斯图便于求这四个元

上下界和确界

（最后一行应该是最大元
注意这时候y∈A，有可能会出现没有上下界的情况

全序关系（任意两个元素都有偏序关系）

良序关系（A的任何一个非空子集都有最小元素，哈斯图呈现扇形）

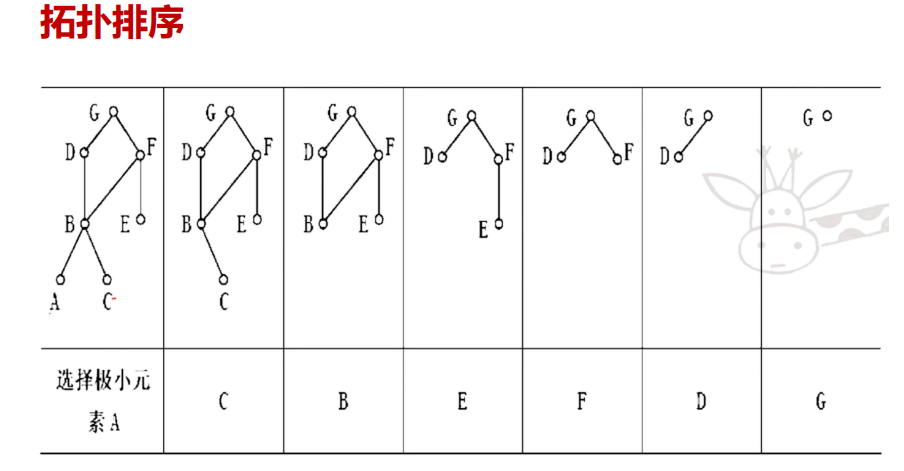
拓扑关系（通过偏序构造全序关系）

（不断删线）