3.24 关系的性质&关系的运算
1 关系的性质
1.1自反性:

非空集合上的空关系是一个全0的矩阵,主对角线上不是全为1,不自反;
如A={2,6,5}R={(2,2),(5,5),(6,6)}称为自反
1.2 证明自反性

恒等关系R={(a,a),a∈A}则称自反,记作I_{A}
所以I_{A}包含于R是R在A上自反的充要条件
1.3 反自反性

关系矩阵中主对角线全为0
实数集上的小于关系,幂集上的真包含关系是反自反的,空集上的空关系是其上的反自反关系(任意集合上的空关系都具有反自反性)
总结: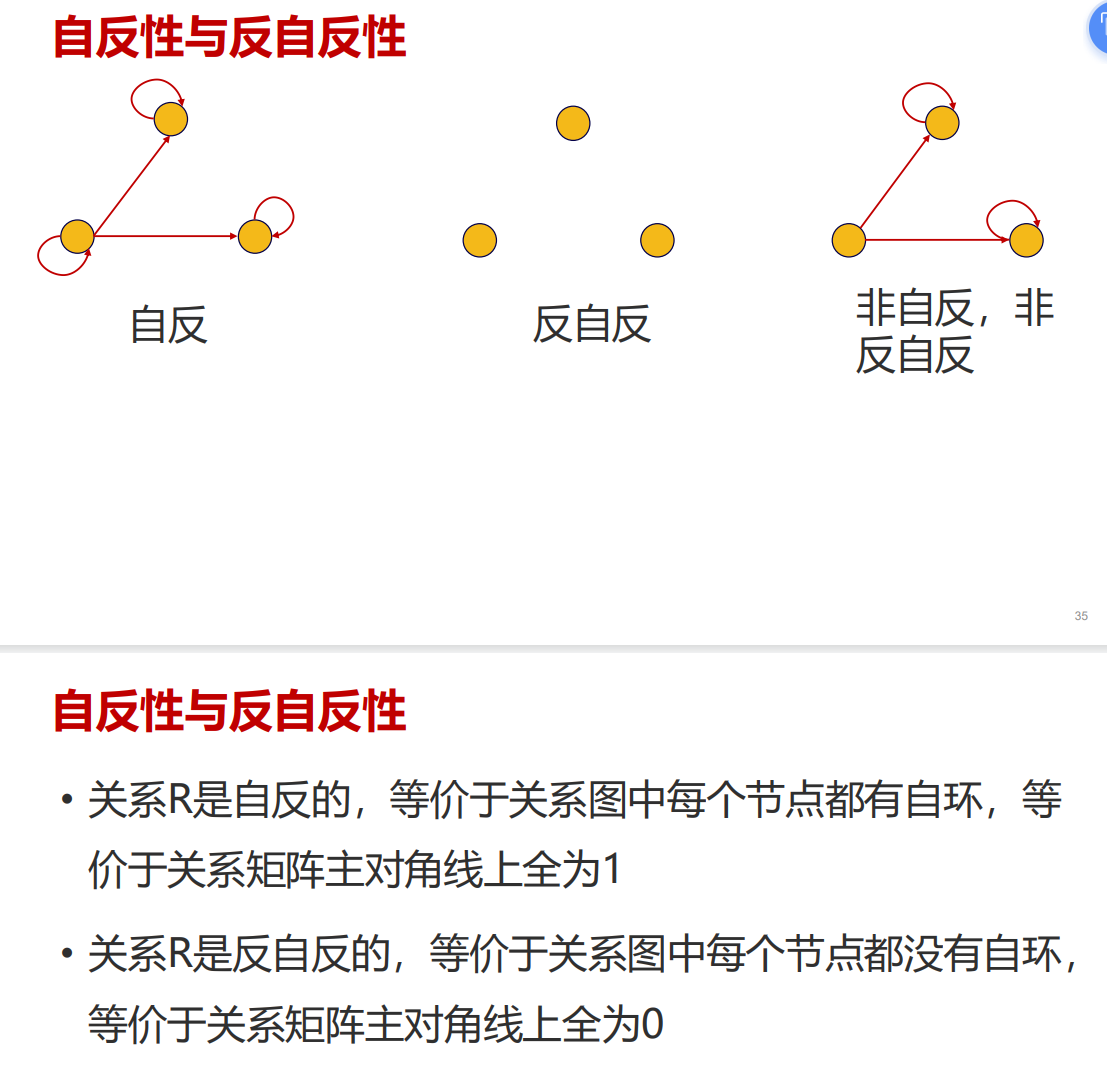
1.4 对称性

关系矩阵是对称矩阵
1.5 反对称性

关系矩阵关于主对角线对称的任意两个元素至多有一个1
关系图:
是否具有对称性看一对节点之间的边(可能既是对称又是反对称)
是否具有自反性看有没有自回环
1.6 传递性

关系图:任意一条长度为2的路径都有从其起始顶点到终止顶点的边
(1,1)也算传递
证明传递性:

(一旦两个顶点出现双向边,看这两个顶点间有没有双向边,如果有,这两个顶点必须有自回环才有双向边)
关系图:
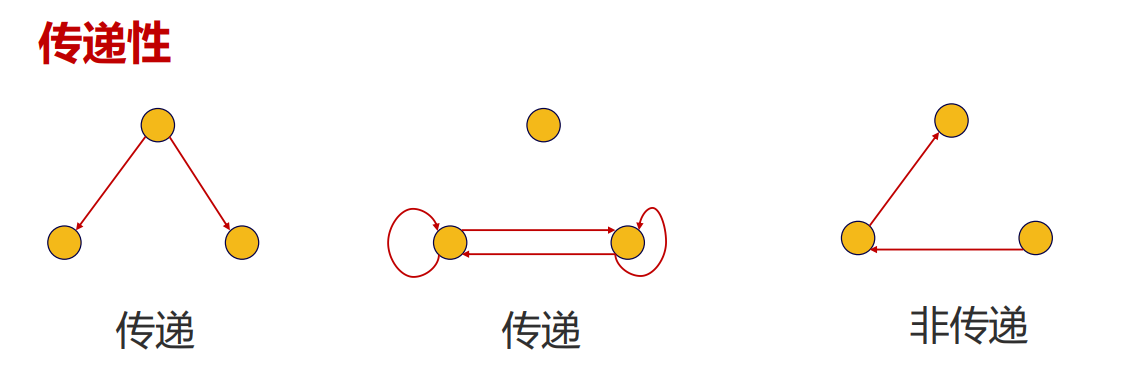
2 关系的运算
2.1 基本运算(并、交、差、补)

2.2 复合关系


做替换(把公共项做替换即可)
2.3 复合运算的性质

满足结合律,不满足交换律

并集的分配律是相等,交集的分配律是包含
证明例题(涉及谓词辖域的收缩和扩张)

通过任取某个元素来证明
证明过程第二行:因为前面的式子没有c,所以 存在c 这个谓词的辖域可以扩大
几个复合符号写几个存在

2.4 复合矩阵的表示(可简单理解为矩阵乘法)(都为0才是0,否则就是1)

R是传递的,当且仅当R^{n}∈R
2.5 幂运算

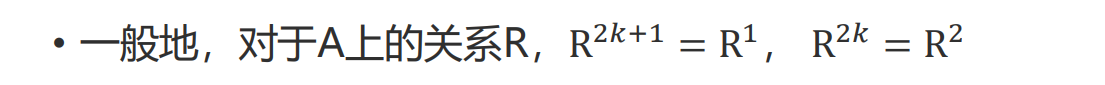
求n次幂肯定有规律
2.6 逆运算

前后颠倒顺序即可
2.7 逆运算的性质

2.8闭包运算


对称闭包

传递闭包

用归纳法证明

warshell算法求传递闭包
闭包的性质

先对称会把矩阵的1变多,然后传递得到的矩阵会更大
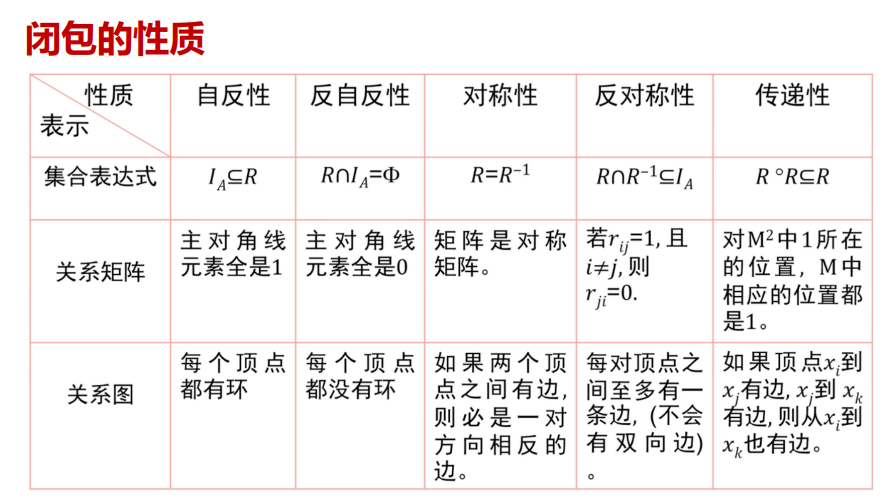
3 关系与有向图(*没啥用)
3.1 有向图的路径

3.2(可以辅助理解R的幂运算,有点用)

R^∞代表这两个元素之间有通路
例子



 浙公网安备 33010602011771号
浙公网安备 33010602011771号