3.22 三重积分计算方法

三重积分的实际意义：计算一个立体的质量（可以）
1 投影法（先一后二）（一个土豆切成土豆丝，最后再累加Dxy平面）
一个立体图形可以看成是两个曲面拼接而成，z=(x,y)可表示一个曲面

假设x和y都是确定的，然后就累加z，最后再算面积分
先假设有一条竖线，注意竖线是从哪里进入，从哪里离开

2 截面法（先二后一）（一个土豆切成土豆片）
把z看成是固定的，计算面积分

适用情形：
1.截面D容易计算面积
2.被积函数只含有自变量Z的函数

画图时可以先把z看成是一个定值，把每一个面画出来

柱坐标变换
先二后一（二变成极坐标）
例题

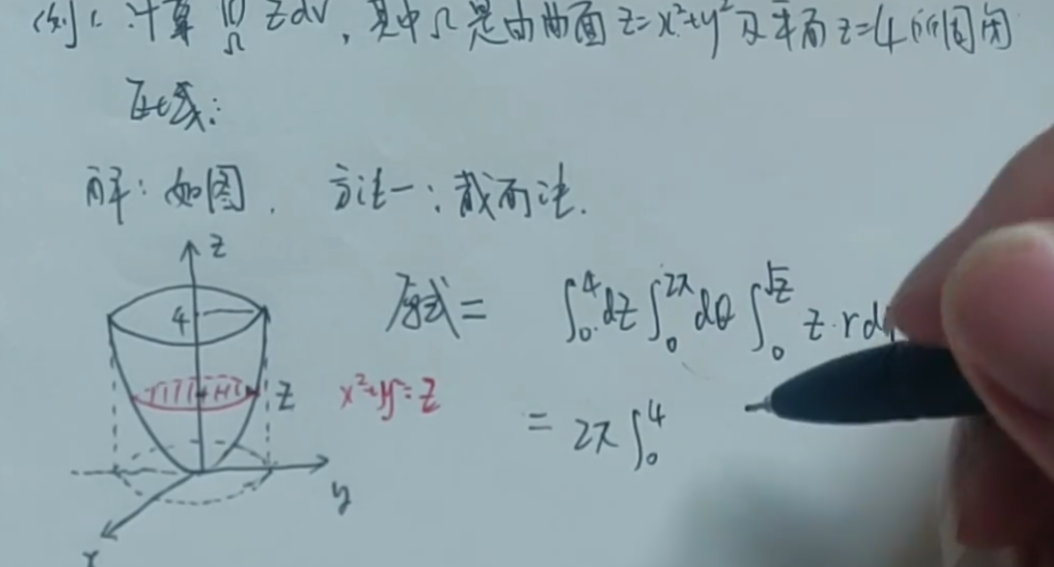
p的范围看投影，两曲线相等

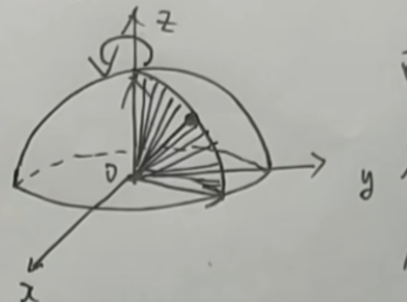
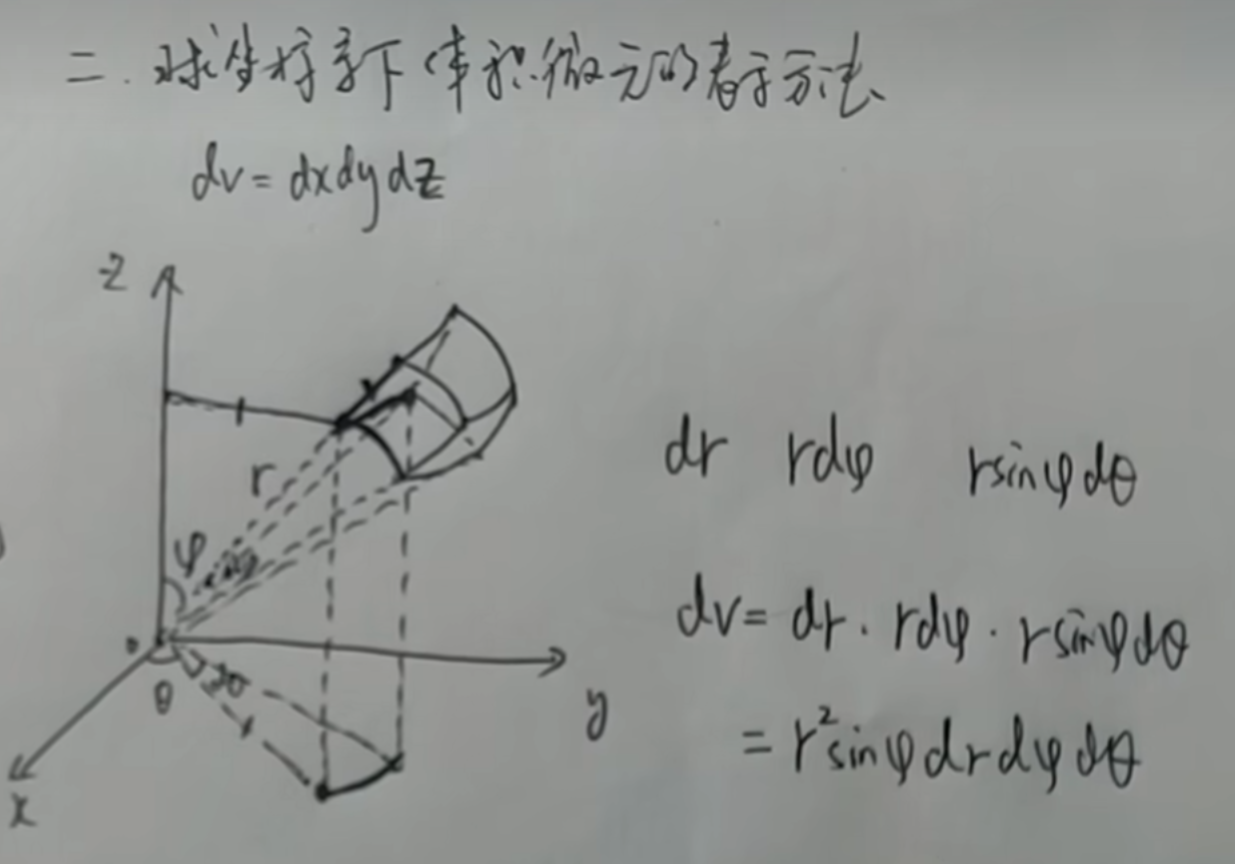
球坐标变换
从原点出发，先求一个面积分，再将这个面绕z轴旋转

与直角坐标系的对比

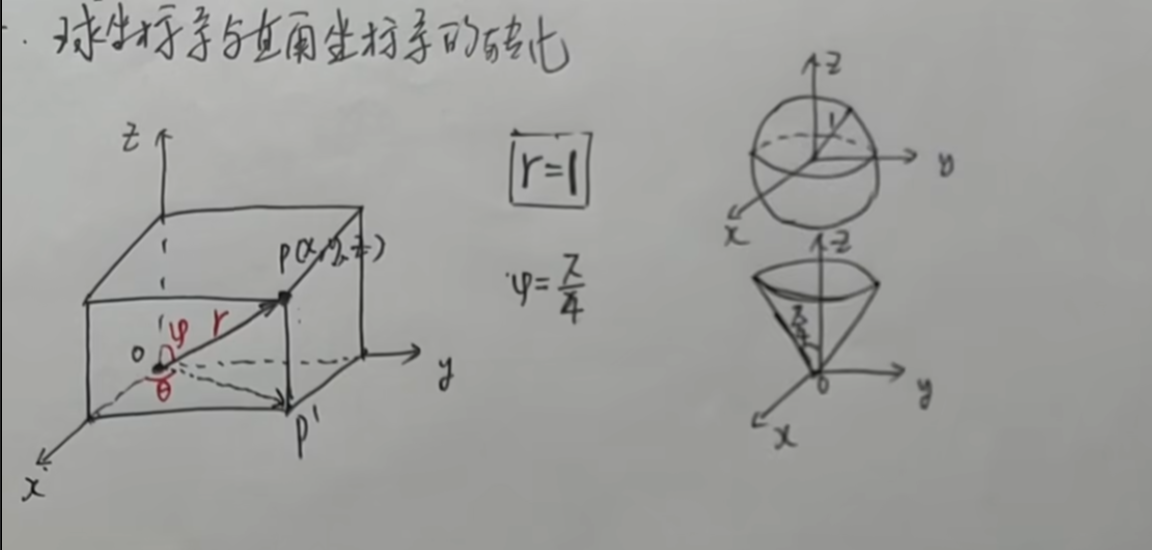
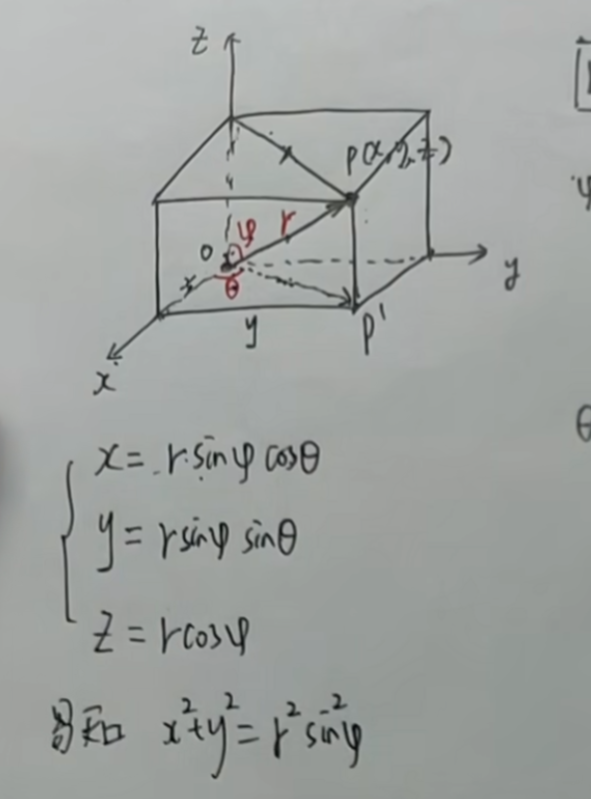
球坐标系在直角坐标系的表示方法

雅可比行列式也可以

先积分r，（确认半圆的半径）、再积分fai，（确认和z轴之间的夹角），最后积分cta（确认绕z轴旋转的角度）

如何确认r:画一条从原点出发的直线
如何确认fai（角度范围0把上述积分绕着z轴旋转~Π）：把上面的射线从z轴开始，旋转（也可以让x=0，在yoz平面上观察）
如何确认cta：把上面的积分绕z轴旋转

做题时可有意识记忆一些常见图形