3.15 回溯法（解决排列组合，子集问题）

1.1
核心思想：当一种可能情况不成立时，往前回退一步
1.2 模板

1 //一定要分成横纵两个方面思考回溯
2 void backtracking(参数) {
3 if (终止条件) {
4 存放结果;
5 return;
6 }
7
8 for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {//注意i=0,i=start的区别
9 处理节点;
10 backtracking(路径，选择列表); // 递归 注意(i)和(i++)的区别 后面会懂
11 回溯，撤销处理结果

1.3 图形理解

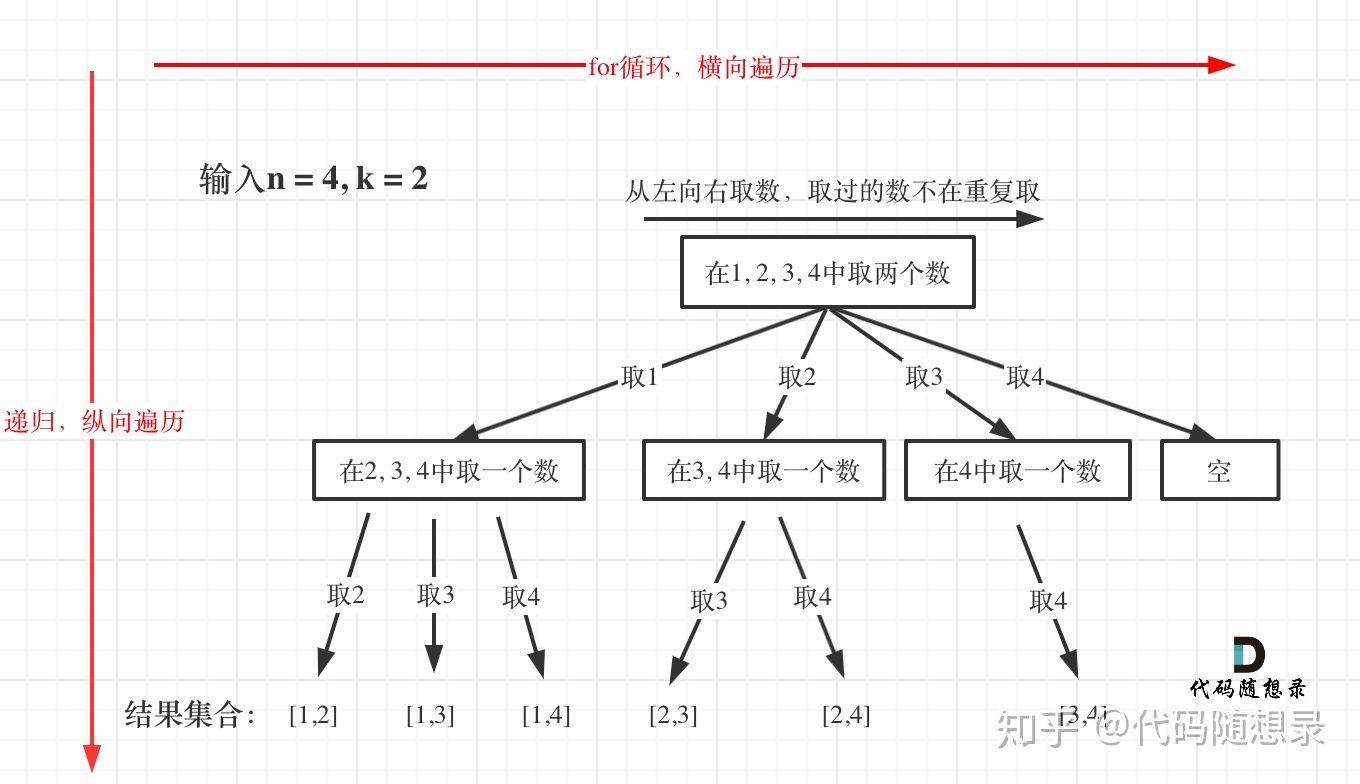
1.4 例题
import java.util.ArrayList;
import java.util.List;

public class Permutations {
public List<List> permute(int[] nums) {
List<List> result = new ArrayList<>();
backtrack(nums, new ArrayList<>(), result);
return result;
}

private void backtrack(int[] nums, List<Integer> path, List<List<Integer>> result) {
    // 终止条件：当路径长度等于数组长度时，说明找到了一个完整的排列
    if (path.size() == nums.length) {
        result.add(new ArrayList<>(path));
        return;
    }

    // 遍历所有可能的选择
    for (int i = 0; i < nums.length; i++) {
        // 如果元素已经被使用过，则跳过
        if (path.contains(nums[i])) {
            continue;
        }

        // 做出选择
        path.add(nums[i]);

        // 递归调用
        backtrack(nums, path, result);

        // 撤销选择
        path.remove(path.size() - 1);
    }
}

}