3.6-3.7 隐函数的偏导数 & 方向导数
1.1 定义
1.1.1 隐函数的定义:如果Z不能用X,Y表示,称为隐函数
1.2 分析
若F(x,y,z)=0;确定Z=z(x,y)
原式=F(x,y,z(x,y)),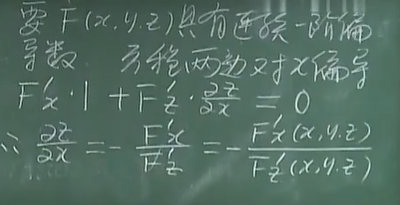
即可得到上图的结论
tip:在外层函数连续的情况下,对哪个变量的偏导数不为0,哪个变量就作为因变量。
1.3 例题
1.3.1 例1(三种解法)
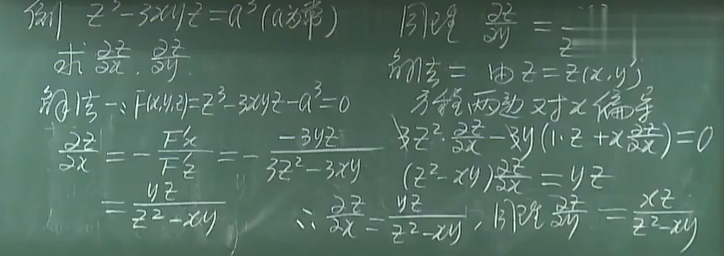
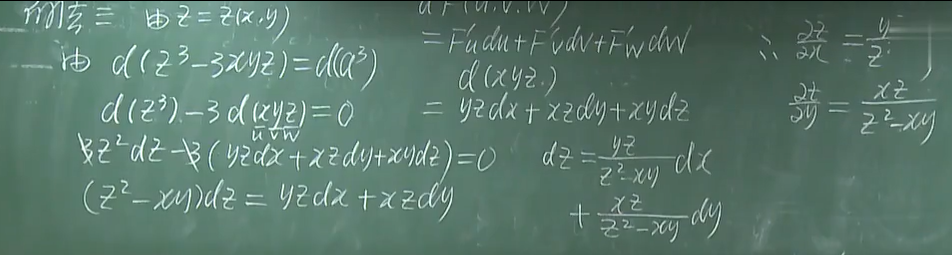
1.3.2 例2 (上一例题中法3(求微分)的优越性)
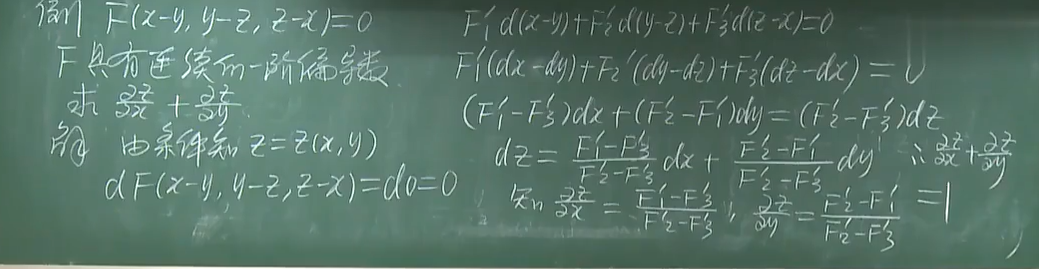
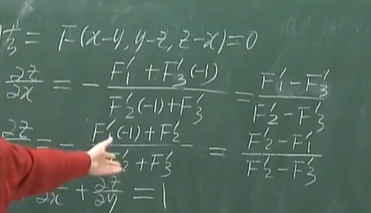
总结:用结论求偏导和用微分求偏导较为方便(即例1的法一和法三)
1.4 方程组确定隐函数求偏导
1.4.1 利用克莱姆法则
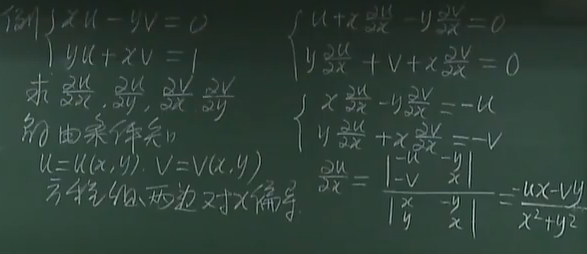
1.4.2 利用微分
微分中dx,dy前面的系数就是某一变量对另一变量求偏导的值
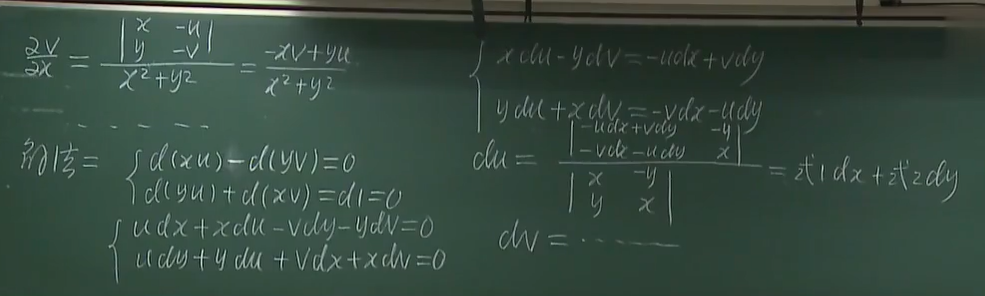
2.方向导数
2.1 定义
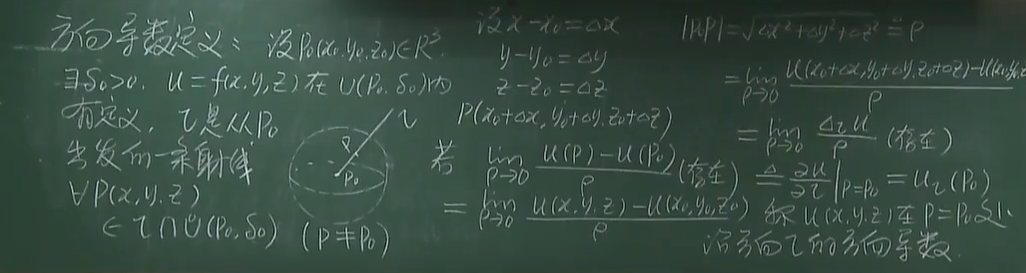
注:函数沿任何方向的方向导数都存在并不能推出该函数偏导数存在(方向导数都是求射线,而偏导数是0+和0-)
2.2 定理(函数在某一点可微即可推出函数在这一点方向导数存在)
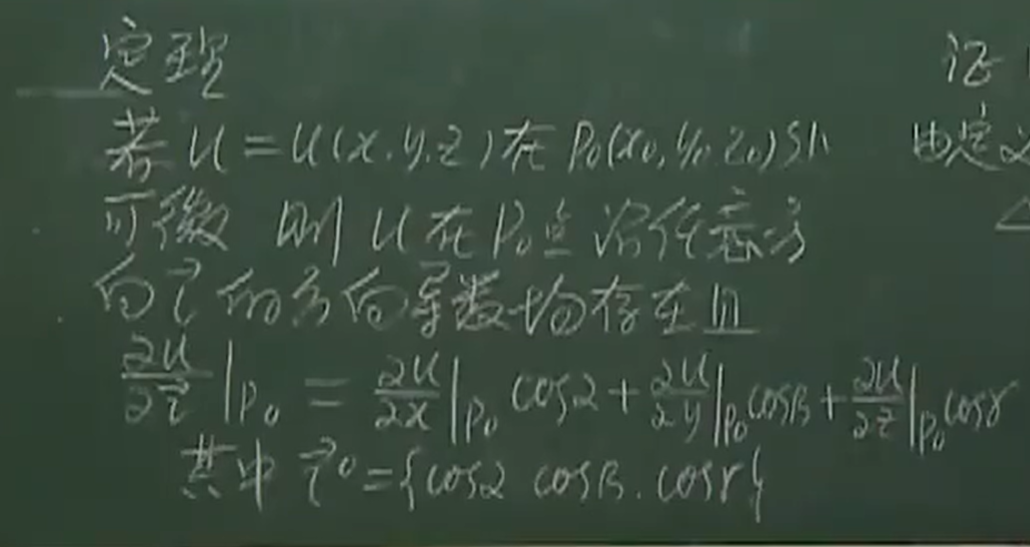
证明过程:
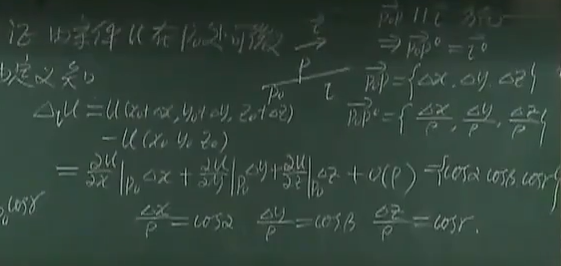
2.3 求
2.3.1 如果求分片函数在孤立点的方向向量一般用方向导数的定义
2.4 梯度
2.4.1 定义
沿梯度的方向导数最大
垂直时为0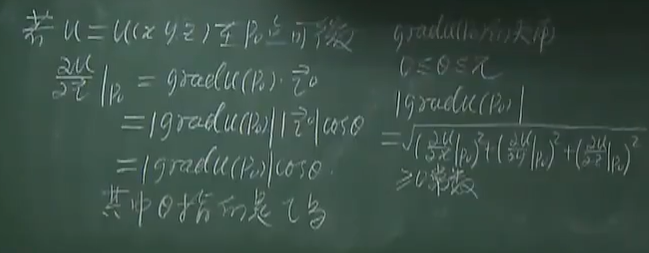


 浙公网安备 33010602011771号
浙公网安备 33010602011771号