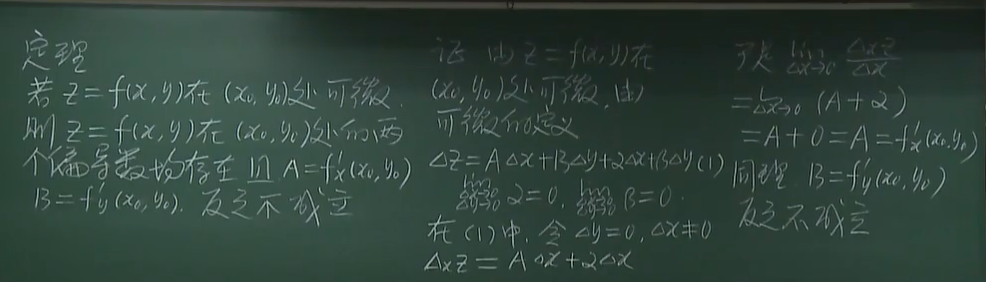3.1 多元函数的全微分
1 多元函数的全微分
1.1 定义
1.1.1 回顾一元函数的微分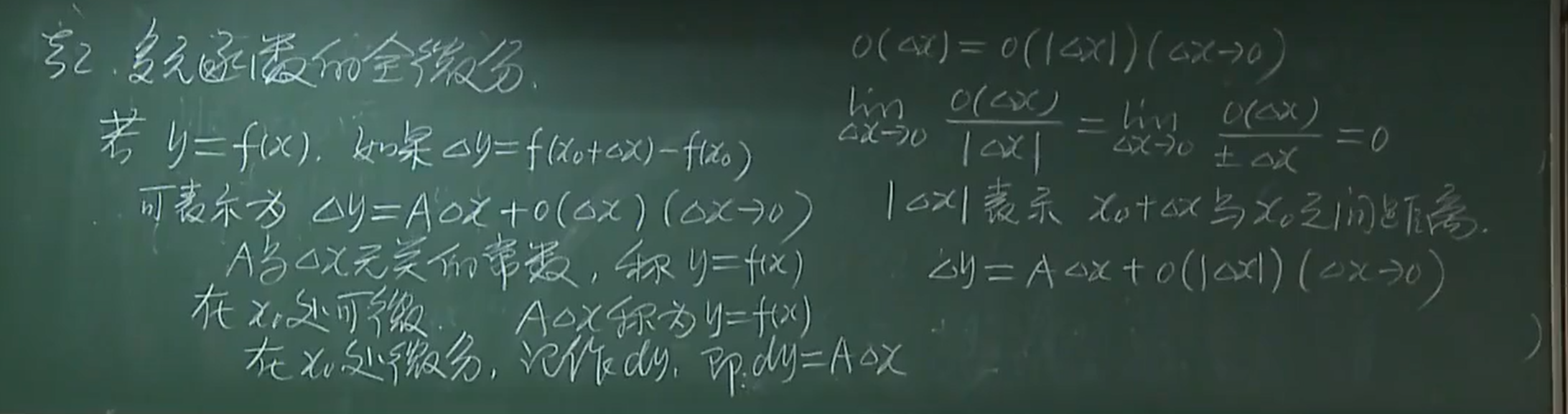
1.1.2 多元函数的定义
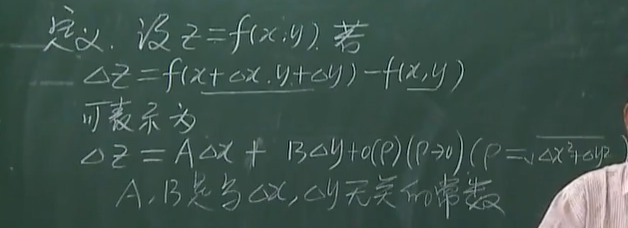
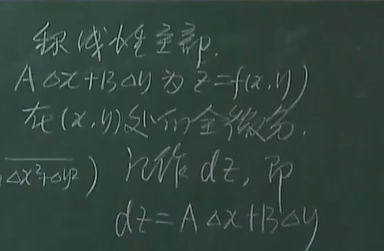
1.1.3 可微推导连续
但连续不一定可微,证明如下:
若连续一定可微,又一元函数必满足二元函数的性质,又一元函数可微必可导,可推至连续必可导,矛盾
1.2 多元函数可微的必要条件
1.2.1 可微必可导&证明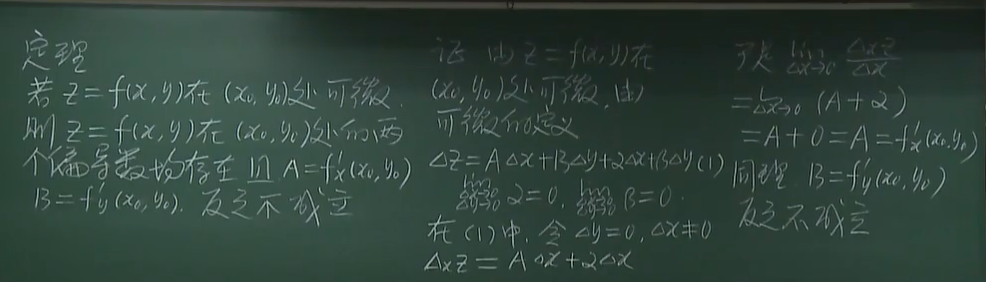
1 多元函数的全微分
1.1 定义
1.1.1 回顾一元函数的微分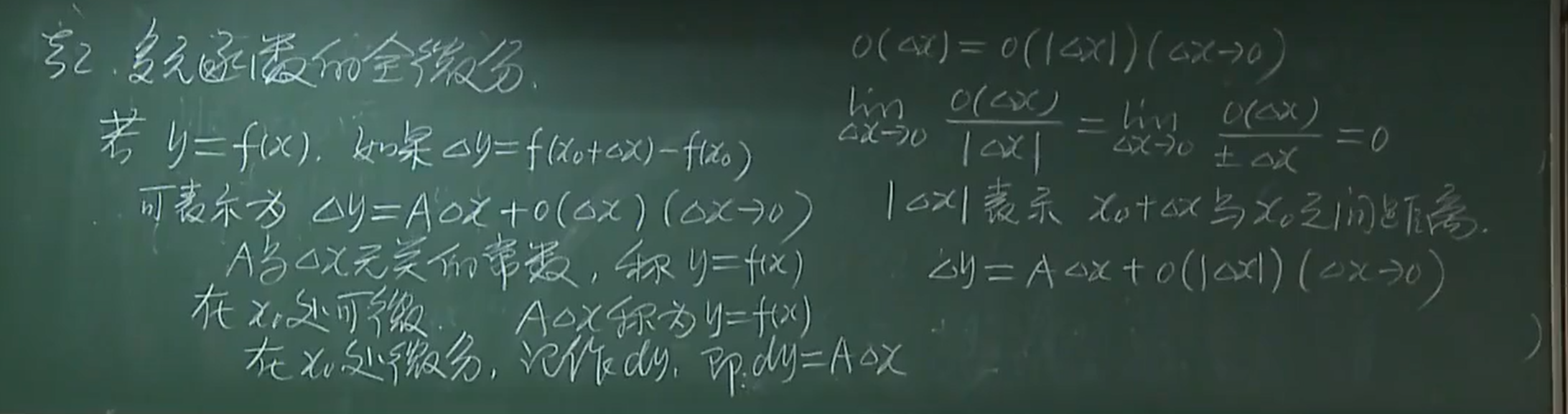
1.1.2 多元函数的定义
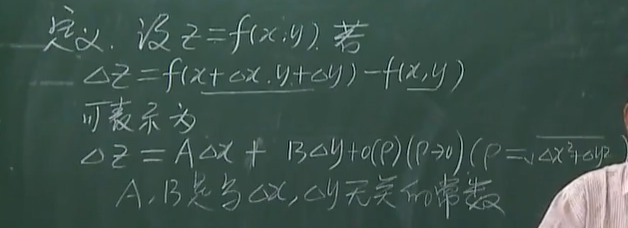
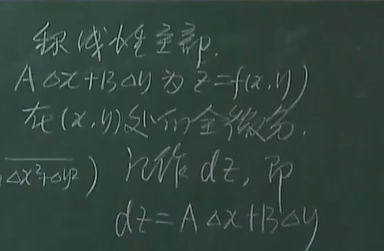
1.1.3 可微推导连续
但连续不一定可微,证明如下:
若连续一定可微,又一元函数必满足二元函数的性质,又一元函数可微必可导,可推至连续必可导,矛盾
1.2 多元函数可微的必要条件
1.2.1 可微必可导&证明