GMOJ 4289. Mancity 题解
义正言辞地吐槽出题人:漏题面就算了,大家一起被坑;数据范围写错也能忍,数据水;但把一道大量细节的题的题解写的如此简陋就实在……
于是有了这一篇又臭又长的东西。
TIPS:由于这篇东西又臭又长,建议先翻到最下面理清楚每一步要干嘛再从上往下看。
约定
- 如无特殊说明,“点 \(i\) ” 指“当前点”或“某个点”。
- “长度”指要走多少小时,“实际长度”指路径上所有边的权值和。
- \(ToRt_i\) 表示 \(i\) 到 \(Root\) 的实际距离。
首先
先要知道两件事:
定理1:路径可逆性,即 \(x\to y\) 的长度和 \(y\to x\) 的长度一样。
定理2: 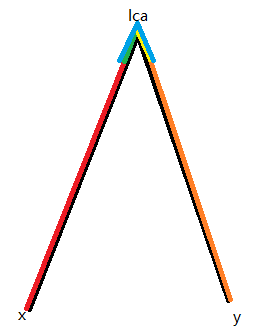
如图,设绿色路径和黄色路径的长度均小于等于 \(d\) (注意,除非没有对应的红色路径或橙色路径,不能是0,原因后面讲),且走完红/橙色路径时水栓不能继续行进,那么 红色路径长度+蓝色路径长度+橙色路径长度 的值与 \(x\to y\) 的答案一样。
证明?没有证明,反正是对的
然后
因为我们有了定理2,所以我们尝试把询问拆成红色路径,橙色路径与蓝色路径来做。
因为有定理1,所以我们假定红色路径和橙色路径都是向上的。于是就有一种显然的方法,倍增每个点向上走的小时数,然后合并即可。但由于毒瘤出题人卡 \(O(nlogn)\) 算法,所以我们寻求优化。
注意到题目没有强制在线,考虑离线。
第一步,我们先求出每个点向上走1个小时能走到哪,设 \(T_i\) 为第 \(i\) 个点向上走1个小时走到的结点,明显的点 \(i\) 的 \(T_i\) 肯定在 \(Root\) 到 \(i\) 的路径上。然后,因为 \(i\) 到 \(FA_i\) 有距离(废话),所以这个点的 \(T\) 一定在 \(T_{FA_i}\) (父亲的 \(T\))到 \(i\) 的路径上。
我们把 \(Root\) 到 \(i\) 的路径用个栈记录一下,然后在这个栈上从 \(T_{FA_i}\) 所在的位置向后枚举一个 \(j\),直到 \(ToRt_i-ToRt_j\le D\) ,此时的 \(j\) 就是 \(T_i\)。因为每个点只会被枚举一次,所以时间复杂度 \(O(n)\) 。
接下来
正片现在开始。
首先我们如果要知道三大路径在哪,我们肯定要知道 \(LCA\) ,同样的,因为出题人卡 \(O(nlogn)\) 算法,所以需要使用离线的Tarjan算法求 \(LCA\)。什么?你不知道求 \(LCA\) 的Tarjan算法?戳我学习
接下来,我们想,对于红色路径,其可以从 \(x\) 跳若干次 \(T_x\) 得到,由于每个点只有一个 \(T\) ,所以 \(T\) 数组本身可以表示一棵树(即 \(T_i\) 表示 \(i\) 的父亲结点),设这棵树为 \(TreeT\)。设 \(x\) 的顶端为 \(Top\) ,因为每跳一次 \(T_x\) 就要消耗1小时,那么红色路径的长度就是在 \(TreeT\) 中 \(x\) 到 \(Top\) 的实际长度。
由于我们不知道 \(Top\) 的具体位置,所以我们不能直接处理。于是再DFS一遍,假设现在有一个点 \(i\) 的 \(T_i\) 为 \(m\) ,那么显然 \(i\) 到 \(m\) 在 \(TreeT\) 中的实际长度就为1。而 \(i\) 在 \(TreeT\) 中的子树上的所有结点到 \(m\) 的长度,就为它们到 \(i\) 的长度+1。 因为 \(TreeT\) 是一棵树,所以可以用并查集维护 \(TreeT\) ,在并查集中额外维护每个结点在 \(TreeT\) 中到 \(Root\) 的实际长度,采用路径压缩时,把其父亲所有点(可以包括 \(Root\),因为其值为0)的这个长度加到自己的长度上再压缩(注意不能使用按秩合并,这样会破坏树的原本结构,路径压缩也破坏,但因为一开始的结构正确,可以维护正确的值)。这样就可以以 \(O(\alpha(N))\) 的时间复杂度维护所有 \(TreeT\) 的结点到 \(Root\) 的答案(实际高些,但无关紧要)。 我们在退出 \(i\) 时,把所有 \(T_j=i\) 的结点合并到 \(i\) 上来再回溯。
因为如果某个点跳过了 \(LCA\) ,跳到的点一定在 \(LCA\) 之上,所以在没有回溯 \(LCA\) 时,不会有点被合并到了 \(LCA\) 的上方。如果现在在 \(LCA\) , \(x\) 和 \(y\) 一定被合并到了 \(LCA\) 下方的某两个结点,这两个结点就是它们分别的 \(Top\) ,由于我们前面已经维护了路径长度,所以只要在并查集中找到 \(Topx\) 和 \(Topy\)(把长度处理出来,同时等会要用),然后取出 \(x\) 与 \(y\) 的额外值,就得到了红色路径和橙色路径的长度。
而对于蓝色路径,可以知道其实际长度一定小于等于 \(2\times D\)。那么如果其实际长度 \(\le D\),其一定花费1小时,如果其实际长度 \(>D\) ,则一定花费2小时(当然有蓝色路径不存在的情况,此时 \(x=y\) ,需要特判一下)。蓝色路径的实际长度明显为 \(ToRt_{Topx}+ToRt_{Topy}-2\times ToRt_{LCA}\) (两个 \(Top\) 到 \(Root\) 的实际长度和\(-2\times LCA\)到 \(Root\) 的实际长度),把三条路径的长度加起来,我们就可以得到答案了。
梳理
程序总流程:
-
Tarjan
-
把 \(T_i\) 设为 \(T_{FA_i}\) (注意现在还是一个栈上的位置)
-
然后求出 \(T_i\) 在栈上哪个位置
-
DFS所有子结点
-
把 \(T_i\) 改为栈上位置对应的点(从栈中取出)
-
处理 \(LCA\)
-
-
把所有的询问挂在 \(LCA\) 上
-
DFS
-
DFS所有子结点
-
处理所有被挂在这个点上的询问
-
把所有 \(T_i=\) 这个点的 \(i\) 合并到当前点上
-
-
输出
至于为什么先处理询问再合并(即黄色路径和绿色路径不能为0),参考下图:
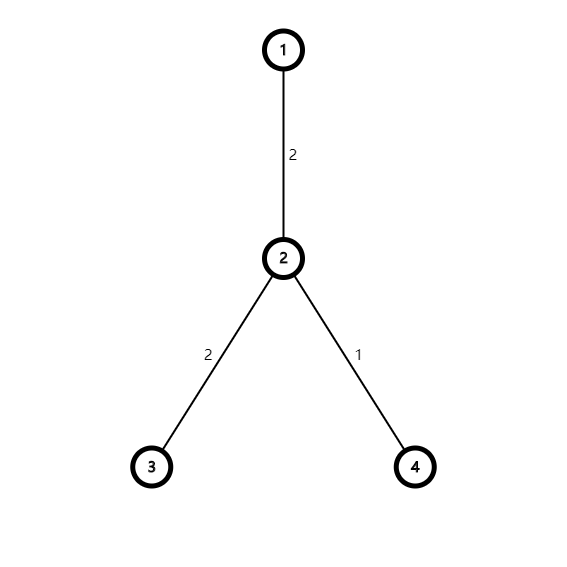
\(D=3\) ,如果询问3 4,而2先把3合并到了2上,那么答案就为1+1(合并+2 \(\to\) 4 的长度),但答案明显是1。而如果不合并,3 \(\to\) 4 的实际长度为3,那么就能求出正确答案。
Code
Warning:丑到离谱
#include<cstdio>
#include<cstring>
#define N 500010
using namespace std;
int n,d,q,fa[N],up[N],ans[N]; //基础信息,up为到父亲边的长度
int last,a[N],b[N<<1][3]; //树,链式前向星
int ques[N][2],qlast,qa[N],qb[N<<1][4]; //询问,仍然是链式前向星,注意被重复利用过
int ct[N],tars[N],lca[N],size,st[N],toup[N]; //ct为T,st为栈,tars为Tarjan用的并查集
int ts[N][2],tlast,na[N],nb[N][2]; //ts为TreeT的并查集,其他是挂在T_i上的点,仍然是……
template<typename T>void read(T &x){
char c=getchar();
for(;c<33;c=getchar());
for(x=0;(c>47)&&(c<58);x=x*10+c-48,c=getchar());
}
void add(int x,int y,int z){ //基础树加边
b[++last][0]=a[x];
b[last][1]=y;
b[last][2]=z;
a[x]=last;
}
void addt(int x,int y){ //TreeT加边
nb[++tlast][0]=na[x];
nb[tlast][1]=y;
na[x]=tlast;
}
void addq(int x,int y,int z,int c){ //挂询问
qb[++qlast][0]=qa[x];
qb[qlast][1]=y;
qb[qlast][2]=z;
qb[qlast][3]=c;
qa[x]=qlast;
}
int root(int m){ //Tarjan用求根
return(tars[m]?tars[m]=root(tars[m]):m);
}
int troot(int m){ //ts用求根
if(ts[m][0]){
int top=ts[m][0];
ts[m][0]=troot(top);
ts[m][1]+=ts[top][1];
return(ts[m][0]);
}
return(m);
}
void uni(int x,int y){ //Tarjan用合并
tars[root(y)]=root(x);
}
void tuni(int x,int y){ //ts用合并
x=troot(x);
y=troot(y);
if(x!=y){
ts[x][0]=y;
ts[x][1]++;
}
}
void tarjan(int m){
st[++size]=m;
toup[m]=toup[fa[m]]+up[m];
for(ct[m]=ct[fa[m]];toup[m]-toup[st[ct[m]]]>d;ct[m]++); //求T的栈上位置
for(int i=a[m];i;i=b[i][0]){
if(b[i][1]!=fa[m]){
fa[b[i][1]]=m;
up[b[i][1]]=b[i][2];
tarjan(b[i][1]);
uni(m,b[i][1]);
}
}
ct[m]=st[ct[m]]; //取出具体点
addt(ct[m],m); //加TreeT边
for(int i=qa[m];i;i=qb[i][0]){ //处理LCA
int get=root(qb[i][1]);
if(get!=qb[i][1]||get==m){
lca[qb[i][2]]=get;
}
}
size--; //记得退栈(我就忘过)
}
void dfs(int m){ //求答案用DFS
for(int i=a[m];i;i=b[i][0]){
if(b[i][1]!=fa[m]){
dfs(b[i][1]);
}
}
for(int i=qa[m];i;i=qb[i][0]){ //处理所有询问
int x=troot(qb[i][1]),y=troot(qb[i][2]),last=toup[x]+toup[y]-2*toup[m];
ans[qb[i][3]]=ts[qb[i][1]][1]+ts[qb[i][2]][1]+(last>0)+(last>d);
}
for(int i=na[m];i;i=nb[i][0]){ //把下方点合并上来
tuni(nb[i][1],m);
}
}
int main(){
freopen("mancity.in","r",stdin);
freopen("mancity.out","w",stdout);
read(n);read(d);read(q);
for(int i=2;i<=n;i++){
int x,y;
read(x);read(y);
add(x,i,y);
add(i,x,y);
}
for(int i=1;i<=q;i++){
read(ques[i][0]);read(ques[i][1]);
addq(ques[i][0],ques[i][1],i,0); //LCA的询问
addq(ques[i][1],ques[i][0],i,0);
}
tarjan(1);
memset(qa,0,sizeof(qa)); //重复利用
qlast=0;
for(int i=1;i<=q;i++){
addq(lca[i],ques[i][0],ques[i][1],i); //把询问挂在LCA上
}
dfs(1);
for(int i=1;i<=q;i++){
printf("%d\n",ans[i]);
}
fclose(stdin);
fclose(stdout);
return(0);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号