CF1662L Il Derby della Madonnina

CF1662L Il Derby della Madonnina

题目描述

有 \(n\) 个点，第 \(i\) 个点在 \(t_i\) 时出现在 \(a_i\) 位置然后消失。你第 \(0\) 秒时在位置 \(0\)，速度为 \(v\)，问最多能赶上多少个点出现。

思路

设 \(dp_i\) 表示到了第 \(i\) 个点，且能赶上点 \(i\) 的时候，最多能赶上多少点，

则 \(dp_j = \max_{i=0}^{j-1}\{ dp_i \space [v \cdot (t_j-t_i) \ge \lvert x_j-x_i \rvert ]\}+1\)。

当 \(i<j\) 有 \(t_i < t_j\)，所以 \(v \cdot (t_j-t_i) = \lvert v \cdot t_j - v \cdot t_i \rvert\)，

可以把限制条件看作点 \(A \space (v \cdot t_i,x_i)\) 与点 \(B \space (v \cdot t_j,x_j)\) 两点的切比雪夫距离为其横坐标的距离，且 \(B\) 在 \(A\) 右侧。画出来图像这样，蓝色区域是 \(B\) 点的限制区域。

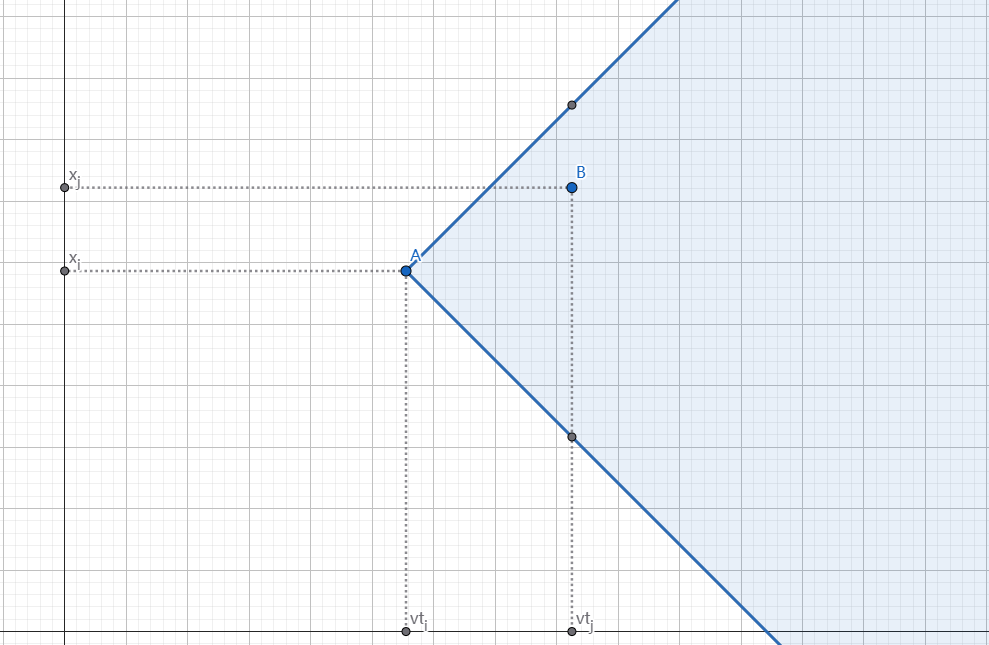
我们发现，\(B\) 点的范围是个边缘与坐标轴夹 $\frac {\pi}{4} $ 的半平面交，这个边缘不与坐标轴垂直很烦，所以我们将坐标系顺时针旋转 $\frac {\pi}{4} $。

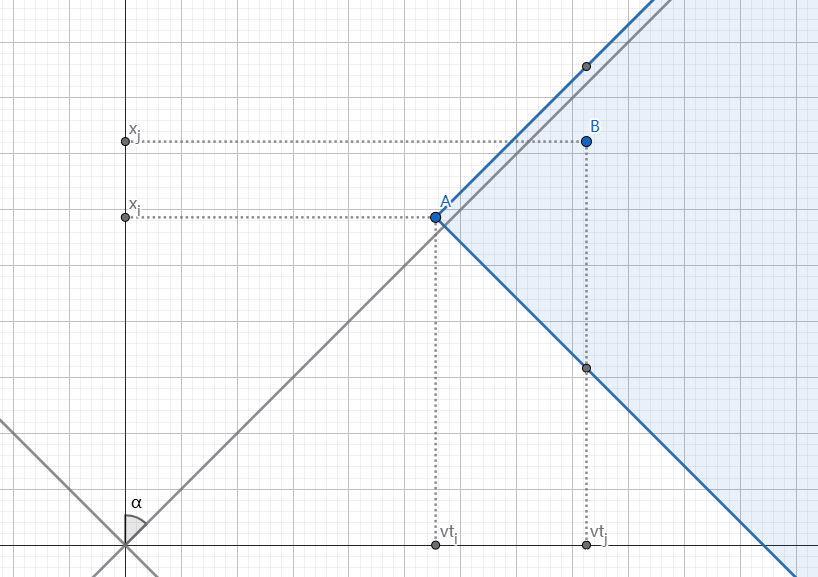
原坐标系 \((x,y)\) 对应新坐标系 \((x\cos(- \frac {\pi}{4} )+y\sin(- \frac {\pi}{4} ),y\cos(- \frac {\pi}{4} ) - x\sin(- \frac {\pi}{4} ))\)。
我们实际只在乎两点间的相对位置，将坐标轴整体扩大 \(\cos(- \frac {\pi}{4} )\) 后不会对限制产生影响。
现在原坐标系的点 \((x,y)\) 对应新坐标系的 \((x-y,x+y)\)。

新坐标系下，\(B\) 的限制变为了需在 \(A\) 的右上部分。

不难发现，原问题变为了求平面最长不下降链，起始点强制为 \((0,0)\)，二维偏序即可。

代码

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 2e5+10;
int n,ans,cnt;
ll v,t[N],a[N],dp[N];
struct node{
	ll x,y;
	inline int operator < (const node&G) const{
		if(x^G.x) return x < G.x;
		return y < G.y;
	}
}g[N];
int main(){

	scanf("%lld%lld",&n,&v);
	for(int i=1;i<=n;++i) scanf("%lld",t+i);
	for(int i=1;i<=n;++i){
		scanf("%lld",a+i); // 求新坐标系下点的坐标
		g[i].x = v*t[i]-a[i];
		g[i].y = v*t[i]+a[i];
	}
	g[++n] = {0,0};
	sort(g+1,g+1+n); // 排序掉第一维
	for(int i=1;i<=n;++i){ // 只留下(0,0)能到达的点
		if(g[i].x>=0 && g[i].y>=0) g[++cnt] = g[i];
	}
	for(int i=1;i<=cnt;++i){ // 第二维求最长不下降子序列
		if(dp[ans]<=g[i].y) dp[++ans] = g[i].y;
		else *upper_bound(dp+1,dp+1+ans,g[i].y) = g[i].y;
	}
	printf("%d",ans-1); // 减去强制选的(0,0)
	
	return 0;
}