「NOI2020」不知道咋记
本来啥也不想写的。我能写点啥?
写我 D1T2 因为线段树上传标记时没取模白给 76 分送走金牌?
写我 D2T2 想到正解然后写假了白给 44 分送走翻盘机会?
金牌线 340+,预计得分 224 + 215 = 439,实际得分 148 + 171 = 319。
啥也别说了,希望 noi 早日改赛制。
本来想写什么 “只要不挂分我也是金牌水平”,不过想想发现大家不挂分其实都是金牌水平,所以这只能说明自己菜。
(p.s.:以上是倒序)
进寝室直接雷击:发现和 jly 一个寝室。
然而我交际水平太差了,所以也没搭上几句话。倒是看到很多人来膜 jly 来着。
突然发现寝室三个人就我没拿金,还各种丢人。
然后是试机 + 笔试日。
笔试看了一遍感觉没啥问题就去看试机题了,试机题有交互,于是今年也会考交互?结果是烟雾弹,今年 6 道传统题。
出成绩了,诶 100 分,那挺好,继续看试机题。看到编译选项 -std=c++11 -O2,全场起立鼓掌.jpg。
本来想写 robot 练练手,结果一不小心就 rm 了所有样例,退役感++。
然后转头写 sequence,发现不会了,退役感++。
然后就是喜闻乐见的 day 1。
这 t1 好不可做啊,诶怎么它 w ≤ 5,诶那不是矩阵乘法就完事儿了吗。
这 t2 好不可做啊,我先来个容斥。诶问题好像没有变简单,算了,先跳。
这 t3 好不可做啊,诶这 t3 是不是严格强于区间逆序对啊,算了,先跳。
然后滚回去写 t1,原本想相信一波 O2 魔法直接硬上矩阵乘法,发现不太科学。
想了一下,我是不是在 noi online 做过一道用向量乘矩阵优化复杂度的题?虽然我当时是用 bitset 莽过去的。
于是改了改发现科学了很多,回去看 t2。
感觉 t2 虽然很容斥,但是其实不管容不容斥,问题的本质都不会变简单。
于是列了一个不容斥的 dp,大概是记 \(dp_{x,i}\) 表示结点 x 往上第一条选中的边深度为 i 的方案数。
诶这个 dp 转移好像是对应位置相乘,那差分后线段树合并就 OK 了?
然后就写了个线段树合并,发现能过样例(竟然能过样例,样例是不是根本不用取模),于是就放着不管了。
然后想了想 T3 发现我还是不会,但是暴力拼盘分好高,于是就开始写暴力。
结果 A 类部分分(区间逆序对)debug 半天不知道错哪儿了,只写了个 \(O(n^2)\) 的 24 分暴力,然后就调到考试结束。
下午查分,打开看到一个 24 分以为是我 T3 的分,冷静仔细观察分析了一下发现我 T2 也是 24 分。
当时心态就崩了。
debug 过后发现了那个没取模的地方,就 10+ byte,白给 76 分。
之后在寝室自闭了一下午 + 一晚上,后来教练拉我出去才勉强能够思考一些事情。
已经发生的既定事实无法改变。
不管怎么拒绝它的发生,不管怎么逃避它的存在,已经发生的既定事实依然无法改变。
我们所能做到的,只有在这事实基础上努力,向着另一条路,向着即使并非之前所期望的路前行。
考 day 2 的时候还是想认真考,至少要证明自己的实力,反正我也不相信自己拿不到银牌。
然后就是喜闻乐见的 day 2。
这 t1 好不可做,会是网络流或者图论建模相关吗。
这 t2。。。这 tm 题面这么长,感觉就像是什么人类智慧题。
这 t3。。。这 tm 不是弦图吗?noi 咋还给整出个弦图了吗?哦,兼职 ctsc 啊,那没事了。
感觉还是 t1 简单些,先看看 t1 好了。
分析了一下发现如果在一道菜用的两种原材料之间建边,可以通过调整使得最优解不包含环。
那当 \(m = n - 1\) 时最优解一定是树,一看发现有这个部分分,感觉这个思路就很对。
猜了几种建树方法,发现每次连最大和最小好像很对。然后如果 \(m > n - 1\) 就反复把最大的拿去单独成菜。
如果 \(m = n - 2\) 就是个背包。算了一下如果用 bitset + 输出方案有点危?
由于 MLE 可能没分,于是决定随机化排列 + 开小点(结果获得了 95 分的好成绩)。
然后看了看 t2 和 t3,发现我弦图知识储备为 0,于是决定开 t2。
想了想什么时候输出 No,大概是存在一条趋于无穷长的链 + 链上长出来一些枝节使得没有给定的树能覆盖这条链。
再一想,诶,这个长出来的枝节是不是要么不长,要么只长出来一个结点(不然肯定不优)?
那么将长/不长表示成 01 串,将给定的树也表示成 01 串。只要没有给定的树对应的 01 串是我们构造的 01 串前缀即可。
那拿个什么数据结构维护一下不就 OK 了吗,反正每个串只会插入/删除一次。
再一想,诶,那树的深度是不是只有 O(log) 啊。草我到底为什么要自己坑自己,都推到这一步了还搞这些飞机。
过了大样例,就没管了。不对啊,不是听说大样例很强吗。
然后开始 t3,发现我连 \(O(n^2)\) 都不会。
盲猜无解就是没有桥;盲猜 A 特性直接最短路;盲猜 B 特性可以 dp(不对这个好像不需要猜)。
结果,t3 的 B 特性直到考试结束也没有调出来。草,怎么感觉我两天干了同一件离谱的事。
考完估分,由于还没察觉到我 t2 的问题于是随口估了个 220 (其实我本来以为 245 遍地走结果发现好像不是这样的?)。
下午查分,发现 t2 果然挂了。不过还是被告知可能有机会,于是稍微期待了一下。
结果,草,要不要这么搞我心态。
话说今年的 D1T2 和 D2T2 是同一个出题人出的?
这个 day1 考挂 day2 差点翻盘的剧本怎么熟悉。诶,这不是去年 yhn 学长省选时的情况吗。
「补题记录」
主要是两天的 t3。t1, t2 的大致思路写在上面(也就是说我考场想到的没啥大问题)。
夭寿啦,数据结构封建王朝复辟啦。
直接分块可以做到 \(O((n+m)\sqrt{n})\),题解中给出了一个 \(O(n\sqrt{m}+(n+m)\log^2 n)\) 的做法:
我们可以对平面分治,则答案可以通过下图(粘自题解)的方法计算:
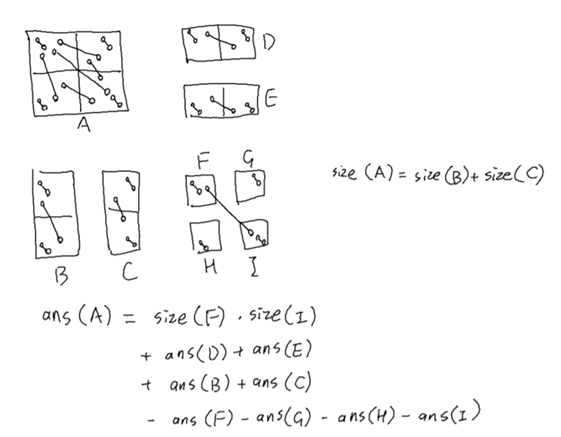
将平面分治的结构(即树套树)存储下来,对于任意询问,可以将询问拆解成 \(\log\times\log\) 个树套树结点:
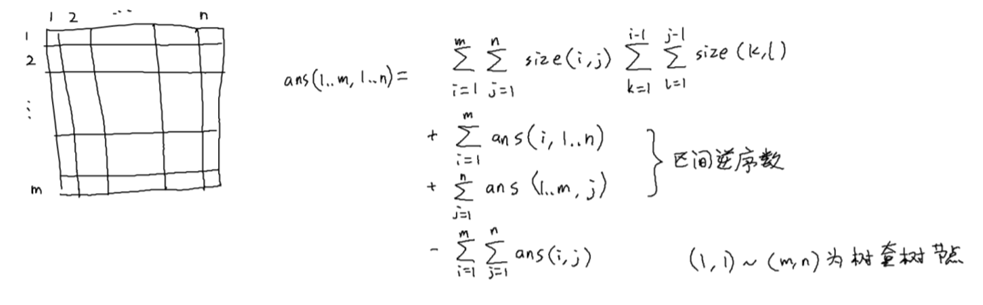
就变成了树套树上的查询 + \(2\log\) 个区间逆序对。
你可能想说:“这不是 \(O(m\sqrt{n}\log n)\) 的做法吗,怎么就给忽悠成 \(O(n\sqrt{m})\) 了呢?”
考虑在某一层有 \(p\) 个元素与 \(q\) 个询问,通过二次离线莫队可以做 \(O(p\sqrt{q})\) 的区间逆序对。那么总复杂度为:
中间的 \(\max\) 表示取最劣情况;可以解得 \(T(n,m)=O(m\log n + n\sqrt{m})\),因此总时间复杂度 \(O(n\sqrt{m}+(n+m)\log^2 n)\)。
不过由于我自带大常数所以目前卡在 88 分(本地测试发现瓶颈在树套树,可能是 \(O(m\log^2n)\) 的内存访问对 cache 太不友好了)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号