《Fundamentals of Computer Graphics》第十章 信号处理

开篇

  在图形学中，我们通常会处理连续变量的函数，比如图像就是这样的例子。但是随着越来越深入地学习，会遇到更多这样的函数。连续函数的本质导致它们不能直接在计算机中被表示，我们只能用有限数量的比特位来表示它们。最好用之一的方法是用函数的采样（Sample）来表示连续函数，即存储函数在不同点的值，然后在需要的时候重建（Reconstruct）点之间的值。
  你现在应该已经熟悉了使用二维像素网格来表示图像这一想法，这实际上就是个采样表示的例子。想象一张图像被数字相机拍摄，在相机的镜面上形成的图像是在图像平面上的位置的连续函数，相机会把连续函数转化为二维样本的网格。从数学上来说，相机把\(\mathbb{R}^2\)类型的函数转化到了\(\mathbf{C}\)即颜色样本的二维数组，或是把\(\mathbb{Z}^2\)类型的函数转化到了\(\mathbf{C}\)。
  另外一个采样表示的例子是平板电脑，当使用触控笔在屏幕上移动时，笔头的位置是随时间连续变化的，但是平板只能在某个时间点测量位置，从而记录到一序列的二维位置。一个动作捕获（Motion Capture）系统做的也是相同的事，通过演员身上的特殊标记连续进行位置测量。上升一个维度到医用CT扫描仪，它会非侵入性地扫描人的身体内部，测量密度关于位置变化的函数，扫描仪输出的结果是三维密度网格。
  这些例子虽然看起来不同，但是可以用相同的数学来解决。不论如何在一个或多个维度上的晶格（Lattice）点采样函数，在任何情况下都要能通过采样获得的样本重建原始的连续函数。
  对于二维图像来说可能有像素就足够了，在相机离散化图像后就不需要考虑原来的连续函数。但是有时我们可能想让屏幕上的图像变大或者变小，特别是用到非整数缩放因子。结果发现最简单的用于实现的算法表现很差，会引入明显的视觉伪影也就是走样（Aliasing）。解释为什么走样发生以及理解该怎么避免这种现象需要采样理论背后的数学。最终得到的算法很简单，不过在它们背后的原理很重要，以及让它们表现良好的细节可能很微妙。
  当然了在计算机中表示连续函数并不是图形学独有的，从数字音频到计算物理学的一些应用场景都有用到采样表示。图形学只是其中之一，用到了里面一些相关的算法和数学。这章将从使用一维数字音频的例子总结采样和重建开始，接着展示一或二维中为采样和重建奠基的基础数学和算法。最后将深入到频域中的细节，它们为这些算法的行为提供了很多见解。

数字音频：在一维中采样（Digital Audio: Sampling in 1D）

  在音频记录中，麦克风会把在空气中以压力波存在的声音转换到随时间变化的电压，转换成的电信号必须被存储来让它能在后续的某个时间被回放。回放涉及到把存储的电信号发送给扬声器，接着扬声器把电信号转化为压力波。
  记录音频信号的数字方法使用采样：一个模数转换器每秒测量几千次电压，生成的整数流能在任意媒介上存储。在回放的时候数据以恰当的速率被读取，被送到一个数模转换器。数模转换器根据输入的数字产生对应的电压，最终产生的电信号和声音输入时记录的电信号一致。下图大致展示了声音采样和重建的过程

  事实证明，好的回放效果所需要的每秒采样数取决于我们要记录的声音的声调。可以良好地还原低音提琴和踢鼓的声音的采样率在回放短笛和铙钹时会产生怪异的声音，当使用更高的采样率时这种问题会消失。为了避免这些欠采样（Undersampling）伪影，数字音频记录器会对输入模数转换器的信号进行滤波，移除那些会导致问题的高频率信号。
  另一种问题发生在输出这边，数模转换器产生的电压会在新样本输入时改变，直到下一个样本前都会保持不变，这样就产生了一种阶梯形的坐标图，这些阶梯的效果就好像噪音，会增加一种高频且依赖于信号的嗡嗡声。为了移除这种重建伪影，数字音频播放器会对数模转换器的输出进行滤波从而让波形变平滑。

采样伪影和走样（Sampling Artifacts and Aliasing）

  相同类型的欠采样和重建伪影也会发生在图形学中的图像或其它被采样的信号中，而且解决方案是一样的即在采样前滤波和在重建后再次滤波。使用过低采样频率会产生问题的一个例子如下

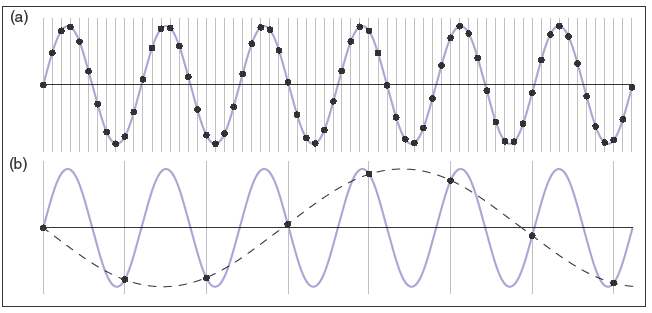
上图展示了使用两个不同的采样频率采样正弦波，上面的为10.8样本每周期，下面的为1.2样本每周期。使用更高采样率得到的样本明显能更好地捕捉信号，使用更低采样率导致了无法很好地重建原信号，反而看起来更像一个低频率的正弦波。
  一旦采样完成了就不知道快和慢的正弦波中哪个是原始信号，因此没有哪一种方法能恰当地在两种情况下重建信号，因为高频信号在“假装”是低频信号，这一现象被称为走样（Aliasing）。
  当采样和重建有缺陷导致在令人惊讶的频率上出现伪影时，走样就会出现。在音频中，走样以额外的怪异音调出现。当一个铃以10KHz响动时，如果以8KHz的频率采样则会产生6KHz的奇怪音调。在图像中，走样以摩尔纹（Moiré patterns）的形式出现，这是采样网格和图像中的常规特征交互的结果。下图是个相关的例子

  另一个在合成图像中走样的例子是熟悉的阶梯式直线，由上图的b图可见。这是一种小尺度特征，会在不同的尺度上产生伪影，对于浅斜率直线来说会产生非常长的阶梯。
  采样和重建的基本的问题可以被简单地理解为特征太小了或太大了，但是这样的话有些更加量化的问题就更难回答，比如

1. 多高的采样率能保证好的效果？
2. 对于采样和重建来说要使用哪种合适的滤波方法呢？
3. 避免走样需要多少平滑度？

卷积（Convolution）

  在我们讨论采样和重建的算法前，我们将首先了解它们基于的叫做卷积（Convolution）的数学概念。卷积是个简单的数学概念，它是用于采样、滤波、重建的算法的基础，此外它还是我们在这章中分析这些算法的基础。
  卷积是作用于函数上的运算，它会取两个函数进行结合，然后得出一个新函数。在这里卷积算子为星号，对函数\(f\)和\(g\)施加卷积的结果为\(f \star g\)，我们称\(f\)与\(g\)卷积，\(f \star g\)为卷积的结果。
  卷积可以作用于连续函数或离散序列，而且不止能用于一维。我们首先从离散的一维情况开始，接着再到连续函数和二维还有三维的函数。为了定义方便，通常假设函数的定义域是无穷的。当然了在实际情况下通常会在一个地方停下，因此我们得用特殊的方法来处理端点情况。

移动的平均（Moving Average）

  为了了解卷积的基本情况，考虑使用移动的平均来平滑一个一维函数，如下图所示

为了在任一点得到一个平滑的值，那么就得计算任意方向\(r\)距离内的函数平均值，距离\(r\)就是平滑操作的半径，它决定到底有多平滑。我们可以使用数学的方法来实现这个想法，如果要平滑一个连续函数\(g(x)\)，平均意味着先求一个区间上的积分，接着再除以区间的长度

\[h(x)=\frac{1}{2r} \int_{x-r}^{x+r} g(t) dt \]

在另一方面如果我们平滑一个离散函数\(a[i]\)，平均意味着先求一定范围索引内的和，接着再除以数值的数量

\[c[i] = \frac{1}{2r+1} \sum_{j=i-r}^{i+r} a[j] \]

这种移动的平均想法是卷积的精髓，不过再卷积中移动的平均是加权的。

离散卷积（Discrete Convolution）

  我们将从卷积的最具体的例子开始，卷积一个离散序列\(a[i]\)与另一个离散序列\(b[i]\)，卷积的结果为另一个离散序列\((a \star b)[i]\)。过程就像使用移动的平均那样来平滑\(a\)，但是这一次会使用\(b\)序列来给每个样本一个权重，而不是使用相同的权重。一个示例图如下所示

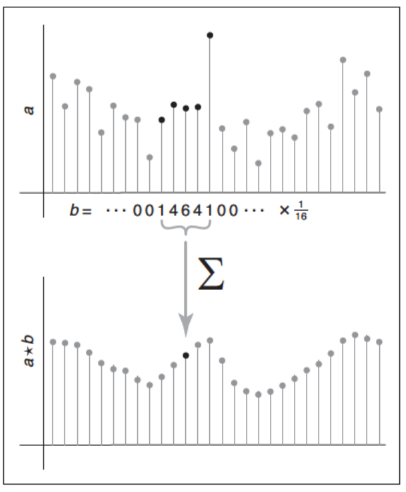
省略掉边界情况可以得到\((a \star b)\)为

\[(a \star b)[i]=\sum_{j} a[j] b[i-j] \tag{1} \]

  看到这里你可能会想这个公式为什么用的是\(b[i-j]\)而不是\(b[-i+j]\)。在信号处理中，卷积可以表示成一个系统对输入信号的响应，这个时候\(b[k]\)表示的是一个输入在发生\(k\)个单位时间后，这个输入对当前输出的影响因子，因此应该使用前者。只不过对于计算机图形学来说，用到的大部分权重序列都是对称的，使用后者在很多时候也能得到正确的结果。
  在计算机图形学中，两个中的一个函数通常有有限的支持，这意味着只有在一个有限的区间内才是非\(0\)的。如果\(b\)有有限的支持且半径为\(r\)，那么当\(|k|>r\)时\(b[k]\)都会等于0。在这种情况下求和表达式可以写为

\[(a \star b)[i] = \sum_{j=i-r}^{i+r} a[j]b[i-j] \tag{2} \]

用伪代码表达则为

卷积滤波器（Convolution Filters）

  卷积非常重要，因为我们能使用它来实现滤波。回顾刚开始的那个移动的平均的例子，实际上可以把平滑操作理解为使用特定的序列进行卷积。当我们计算有限范围内的平均值时，实际上使用的是一个在范围内有相同值其它地方都为\(0\)的权重序列。这种在区间内有常量其它地方为\(0\)的滤波器叫方框滤波器（Box Filter）。对于一个有着半径\(r\)的方框滤波器来说，权重为\(1/(2r+1)\)，因此

\[b[k]= \begin{cases} \frac{1}{2r+1}, -r \leq k \leq r \\ 0, 其它情况 \end{cases} \]

就像这个例子一样，卷积滤波器通常都被设计来让它们的总和为\(1\)，这样就不会影响信号的总体水平。对于滤波的简单例子来说，信号可以是阶跃函数（Step Function）

\[a[i] = \begin{cases} 1,i \geq 0 \\ 0,i<0 \end{cases} \]

滤波器可以是中心在\(0\)的五点方框滤波器

\[b[k] = \frac{1}{5} \begin{cases} 1,-2 \leq k \leq 2 \\ 0,其它情况 \end{cases} \]

对于\((a \star b)[i]\)的计算来说，可以理解为先将\(b\)绕中心进行反转，接着再往右平移\(i\)个单位，然后求\(a\)序列与反转并平移后的\(b\)序列的每个元素之间的乘积的总和，直到超出滤波半径\(r\)。下面是一个形象的示例图

卷积的属性（Properties of Convolution）

  看到这里，你会感觉卷积似乎是个不对称操作，\(a\)序列是要被平滑的，而\(b\)序列会提供权重。实际上反过来也是有效的，也就是说滤波器和信号之间是可互换的。证明这一点很简单，之前说过在相乘求总和前要进行的操作是：对滤波器\(b\)进行反转然后再平移，这个时候你就会发现这两个操作实际上是相对的，我们完全可以把\(a\)绕中心进行反转，接着再往右平移\(i\)个单位，然后求反转并平移后的\(a\)序列与\(b\)序列的每个元素之间的乘积的总和。因此可以得到卷积表达式还可以为

\[(a \star b)[i] = \sum_{k} b[k] a[i-k] \tag{3} \]

这和\((1)\)式简直长得一模一样。因此对任意\(a\)序列和\(b\)序列可以得到\((a \star b)=(b \star a)\)，我们称卷积为交互运算。更一般地说，卷积类似乘法操作，有着交换律和结合律，此外对加法来说还有分配律。因此有下面的关系

\[\begin{align*} (a \star b)[i] &= (b \star a)[i] \\ (a \star (b \star c))[i] &= ((a \star b) \star c)[i] \\ (a \star (b+c))[i] &= (a \star b + a \star c)[i] \end{align*} \]

  此外在离散卷积中有一种简单且特殊的滤波器\(d\)，它会使\((a \star d)[i] = a[i]\)。这里你可能很快就想到了，离散序列\(d\)应该长这样

\[d[k] = \begin{cases} 1,k=0 \\ 0,k \neq 0 \end{cases} \]

事实上它通常被称为克罗内克\(\delta\)或单位冲激序列。

用移位的滤波器进行卷积（Convolution as a Sum of Shifted Filters）

  \((1)\)式描述的卷积操作可以被理解为把滤波器反转并移动到\(i\)索引处，计算\(i\)索引处周围的信号对\((a \star b)[i]\)的影响。除了这样还可以被理解为对于每个\(j\)索引处的信号，把滤波器反转并移动到\(j\)索引处，计算这个信号对周边\(i\)索引处\((a \star b)[i]\)的影响。下方有个形象的示例图

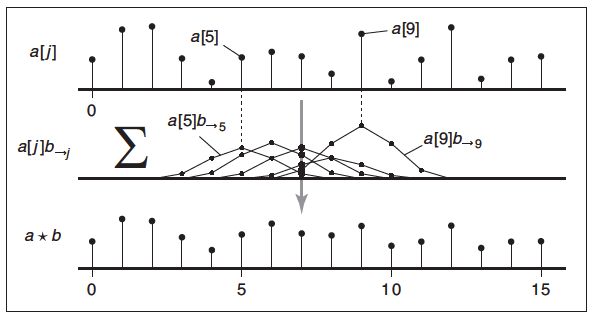
  把滤波器反转并移动到\(j\)索引处，求得\(j\)索引处的信号\(a[j]\)对\(i\)索引处\((a \star b)[i]\)的影响因子为\(b[i-j]\)，上述操作可以被写为\(b_{\rightarrow j}[i]\)，这样可以得到\((1)\)式的另外一种表达形式为

\[(a \star b)[i] = \sum_j a[j] b_{\rightarrow j}[i] \]

卷积连续函数（Convolution with Continuous Functions）

  在计算机程序中要处理的大多都是离散序列，采样后的序列都是被用来表达连续函数的，不过我们应该也要了解下连续函数的卷积。对于连续函数的卷积我们很容易能得出公式，只需要把\((1)\)式的求和形式替换成积分形式，即

\[(f \star g)(x) = \int_{-\infty}^{+\infty} f(t) g(x-t) dt \tag{4} \]

看到这个公式可以想象一个被反转的滤波器\(g\)正在跟随\(x\)滑动，在某一刻计算的\(\int_{-\infty}^{+\infty} f(t) g(x-t) dt\)就是\((f \star g)(x)\)。和离散卷积一样，连续函数的卷积服从交换律和结合律，对加法来说也有分配律。之前提到的对离散卷积的理解也能完全应用于连续函数的卷积，就比如

\[(f \star g)(x) = \int_{-\infty}^{+\infty} f(t) g_{\rightarrow t}(x) dt \]

假如\(f\)为方框函数

\[f(x) = \begin{cases} 1,-\frac{1}{2} \leq x < \frac{1}{2} \\ 0,其它情况 \end{cases} \]

由\((4)\)式可得

\[(f \star f)(x) = \int_{-\infty}^{\infty} f(t) f(x-t) dt \]

由于\(f\)这个函数很特殊，用之前讲的使用滑动来理解连续函数的卷积的方法，会发现\(f\)与它自己的卷积实际上就是看有多少面积是重叠的。当\(x\)从\(0\)开始线性增加或减少时，重叠的面积会线性减少。因此很容易得到卷积后的新函数

\[(f \star f)(x) = \begin{cases} 1-|x|,-1<x<1 \\ 0,其它情况 \end{cases} \]

这个函数被称为帐篷函数（Tent Function），是另外一个常见的滤波器，下方为这个函数的示例图

狄拉克\(\delta\)函数（The Dirac Delta Function）

  正如之前提到的克罗内克\(\delta\)一样，连续函数的卷积中也存在类似的东西。它叫狄拉克\(\delta\)函数，这个函数描述了一个位于\(x=0\)处的极窄尖峰，对于所有\(x \neq 0\)来说都有\(\delta(x) = 0\)，它在\(x=0\)时的函数值也没有明确的定义。但是有

\[\int_{-\infty}^{+\infty} \delta(x) dx = 1 \]

正因为这样所以有

\[(\delta \star f)(x) = \int_{-\infty}^{+\infty} \delta(t) f(x-t) dt = f(x) \]

离散与连续的卷积（Discrete-Continuous Convolution）

  有两种方法能连接离散和连续的世界，第一种是采样，即在整数参数时记录连续函数\(f(x)\)的数值，然后省略掉其他部分，这样我们就通过\(a[i]=f(i)\)把连续函数\(f(x)\)转换到了离散序列\(a[i]\)。
  从另一个方向来，把离散的函数或序列转化为连续函数，叫重建。这是使用另外形式的卷积做到的，在这种情况下我们使用一个连续的滤波器\(f(x)\)对一个离散的序列\(a[i]\)进行滤波

\[(a \star f)(x) = \sum_{i} a[i] f(x-i) \]

重建后的函数\(a \star f\)在\(x\)的值是在\(x\)附近的每个样本加权后的总和，权重来自滤波器\(f\)。下方是一张相关的示例图

  要注意的是，对于离散与连续的卷积，我们一般把序列写在前面，以便让求和在整数范围内进行。和离散卷积一样，如果求和有范围也就是知道滤波器的半径\(r\)，这样我们就只需要计算范围内的样本的影响

\[(a \star f)(x) = \sum_{i=\lceil x-r \rceil}^{\lfloor x+r \rfloor} a[i] f(x-i) \]

这里要注意的是，当一个点离\(x\)的距离正好为\(r\)时，它将不会被算在求和内。这和离散的情况相反，因为离散的情况会包含这样的点。下面给出实现上方公式的伪代码。

  和之前说的用移位的滤波器进行卷积一样，离散与连续的卷积的公式也有另一种形式，即

\[(a \star f)(x) = \sum_{i} a[i] f_{\rightarrow i}(x) \]

离散与连续的卷积和样条有着密切的关系，对于均匀样条来说，它的参数化曲线正是样条的基函数和控制点序列的卷积。

在一维以上进行卷积（Convolution in More Than One Dimension）

  至此，关于采样和重建所说的一切都是在一维上的进行的。在图形学中，采样和重建的很多重要的应用都是在二维上进行的，就比如二维图像。幸运的是采样算法和理论可以从一维推广到二维和三维，而且到更远的维度从概念上来说很简单。
  从离散卷积的定义开始，我们可以使用嵌套求和推广到二维

\[(a \star b)[i,j] = \sum_{i^\prime} \sum_{j^\prime} a[i^\prime,j^\prime] b[i-i^\prime,j-j^\prime] \]

如果\(b\)是个有着半径\(r\)的有限支持的滤波器，那么有

\[(a \star b)[i,j] = \sum_{i^\prime=i-r}^{i+r} \sum_{j^\prime=j-r}^{j+r} a[i^\prime,j^\prime] b[i-i^\prime,j-j^\prime] \]

使用伪代码表达有

继续进行推广可以得到在二维中的连续与连续的卷积和离散与连续的卷积

\[(f \star g)(x,y) = \int \int f(x^\prime,y^\prime) g(x-x^\prime,y-y^\prime) dx^\prime dy^\prime \]

\[(a \star f)(x,y) = \sum_{i} \sum_{j} a[i,j] f(x-i,y-j) \]

卷积滤波器（Convolution Filters）

  我们现在已经掌握了卷积的机制，那么可以看看那些在计算机图形学中被常用的滤波器。下面的滤波器都有一个自然半径，它是默认大小用于间隔为一个单位的那些样本的采样和重建。在这个部分，将使用自然大小定义滤波器。比如对于方框滤波器来说，它的自然半径为\(1/2\)。此外还让每个滤波器的积分为\(1\)，因为采样和重建不能改变信号的平均值。
  后面的一些部分提到的应用会要求滤波器有不同的大小，我们可以通过缩放基础的滤波器得到，对于滤波器\(f(x)\)，如果有缩放因子\(s\)我们可以得到缩放后的滤波器\(f_s(x)\)

\[f_s(x)=\frac{f(x/s)}{s} \]

一些卷积滤波器（A Gallery of Convolution Filters）

方框滤波器（The Box Filter）

  方框滤波器是个分段常量函数，它的积分为\(1\)。如果作为一个离散的滤波器，它可以被写作

\[a_{\mathrm{box},r}[i] = \begin{cases} 1/(2r+1),|i| \leq r \\ 0,其它情况 \end{cases} \]

这里要注意为了对称性应该包括端点。如果作为一个连续的滤波器，它可以被写作

\[f_{\mathrm{box},r}(x) = \begin{cases} 1/(2r),-r \leq x < r \\ 0,其它情况 \end{cases} \]

在这种情况下应该排除一个端点，这样能确保方框的半径为\(0.5\)，可以被用作一个重建滤波器。这是因为方框滤波器是不连续的，因此边界情况很重要，对于这种特殊的滤波器，我们应该关注它们。方框滤波器的自然半径\(r=\frac{1}{2}\)。下图为这个滤波器在离散和连续的情况下的示例图

帐篷滤波器（The Tent Filter）

  帐篷或线性滤波器是个连续且分段的线性函数

\[f_\mathrm{tent}(x) = \begin{cases} 1-|x|,|x|<1 \\ 0,其它情况 \end{cases} \]

它的自然半径为\(1\)。对于这个滤波器来说，它是\(C^0\)连续的，即函数值不会跳跃，我们不需要分开定义它的离散滤波器和连续滤波器，因为离散滤波器只是连续滤波器在整数的采样。下方是这个滤波器的函数示意图

高斯滤波器（The Gaussian Filter）

  高斯函数，通常也被称作正态分布，它在理论和实践上都是重要的滤波器。在这章的后面将会看到它的一些特殊属性

\[f_{g,} \sigma(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-x^2/2\sigma^2} \]

参数\(\sigma\)叫标准差，对于这个滤波器来说取一系列的\(\sigma\)都很有用。此外这个滤波器没有自然半径，而且通常没有有限支持的半径，但是由于它是指数衰减的，它的值会飞快地减小到可以被忽视。当有需要的时候，我们可以取半径\(r\)并让外面的函数值都为0，这样可以省去很多影响不大的计算。这意味着滤波器的宽度和自然半径可以由实际应用场景来决定，在实践的时候可以让\(\sigma\)和\(r\)作为滤波器的属性，当滤波器被声明的时候就固定下来，剩下的就是调整缩放因子\(s\)。下方是这个滤波器的示例图

三次B样条滤波器

  很多滤波器都是用分段多项式定义的，而三次滤波器有四段，通常被用于重建滤波器。一个这样的滤波器被称为B样条滤波器，因为它的起源就是作为样条曲线的混合函数

\[f_{B}(x) = \frac{1}{6} \begin{cases} -3(1-|x|)^3+3(1-|x|)^2+3(1-|x|)+1, -1 \leq x \leq 1 \\ (2-|x|)^3,1 \leq |x| \leq 2 \\ 0,其它情况 \end{cases} \]

在三次分段曲线中B样条曲线是特殊的，因为它是\(C^2\)连续的，也就是说它的一阶导数和二阶导数都是连续的。一个更加简洁的定义它的方法为\(f_B = f_\mathrm{box} \star f_\mathrm{box} \star f_\mathrm{box} \star f_\mathrm{box}\)。下方为这个滤波器的示意图

三次Catmull-Rom样条滤波器

  另一个以样条命名的三次分段滤波器为Calmull-Rom滤波器，它在\(x=-2,-1,1,2\)时为\(0\)。当被用于重建滤波器时，这种特殊性质会让卷积后的函数依然过样本点。

\[f_{C}=\frac{1}{2} \begin{cases} -3(1-|x|)^3+4(1-|x|)^2+(1-|x|),-1 \leq x \leq 1 \\ (2-|x|)^3-(2-|x|)^2,1 \leq |x| \leq 2 \\0,其它情况 \end{cases} \]

下面是这个滤波器的一个示例图

Mitchell–Netravali三次滤波器

  对于所有重要的重采样图像应用，Mitchell和Netravali对三次滤波器做了一个研究，并推荐了一个介于前两个滤波器之间的滤波器作为最佳的综合性选择。实际上就是前两个滤波器的加权的和

\[\begin{align*} f_M(x)&=\frac{1}{3}f_B(x)+\frac{2}{3}f_C(x) \\ &= \frac{1}{18} \begin{cases} -21(1-|x|)^3+27(1-|x|)^2+9(1-|x|)+1,-1 \leq x \leq 1 \\ 7(2-|x|)^3-6(2-|x|)^2,1 \leq |x| \leq 2 \\ 0,其它情况 \end{cases} \end{align*} \]

下方为这个滤波器的示意图

滤波器的性质

  滤波器有一些传统的术语伴随着它们，我们可以用这些术语来描述滤波器并且在滤波器之间进行比较。滤波器的脉冲响应（Impulse Response）只是函数的另一个名称，它是滤波器对只包含脉冲的信号的响应。
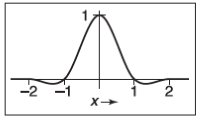
  当一个连续的滤波器有插值性（Interpolating）时，如果被用于与离散序列卷积的重建，卷积后的函数依然会过原始样本点，而不是会接近原始样本点。具有这种性质的滤波器要求\(f(0)=1\)，此外对于任何\(i \neq 0\)的整数都有\(f(i)=0\)。一个示例图如下方所示

  一个有负值的滤波器会有振铃效应（Ringing）和过冲（Overshoot），也就是说会在被滤波的函数急剧变化的地方产生额外的振荡。比如Catmull-Rom滤波器两边都有取负值的地方，如果使用它来滤波一个阶跃函数，则会略微凸显阶跃，造成低于\(0\)的欠冲和高于\(1\)的过冲，下方有个示例图

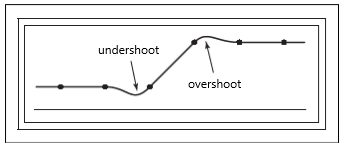
  当一个滤波器被用于重建滤波器并滤波常量序列时，如果滤波后的函数没有数值上的波动，则称这个滤波器是无波动（Ripple Free）的。下方是一个相关的示例图

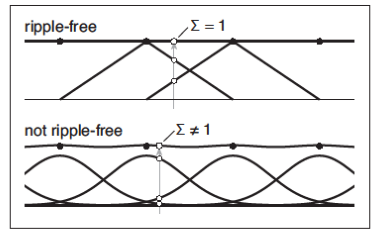
这实际上是要求

\[\sum_i f(x+i)=1 \quad 对于所有x \]

除高斯滤波器外，上个部分提供的所有滤波器在他们的自然半径处都是无波纹的。当它们被用于非整数范围时，无波纹实际上是非必要的。如果有必要消除离散与连续的卷积的波纹时，处理方法也很简单，直接把加权求和的值除以权重总和即可

\[(\overline{a \star f})(x) = \frac{\sum_i a[i] f(x-i)}{\sum_i f(x-i)} \]

  一个连续的滤波器有一个连续度（Degree of continuity）,实际上就是反复求导看导数是否存在以及是否连续。对于方框滤波器来说，它的函数值是不连续的，因此没有连续度。对于帐篷滤波器来说，函数值是连续的但是导数不连续，因此它只有\(C^0\)的连续度。一个滤波器如果有连续的导数，就像之前的部分提到的三次分段滤波器一样，那么就有\(C^1\)的连续度。当然了B样条实际上有\(C^2\)的连续度。当一个滤波器被用作重建滤波器时它的连续度很重要，因为重建后的函数会继承滤波器的连续度。

可分离的滤波器（Separable Filters）

  目前我们只讨论了些用于一维卷积的滤波器，但是对于图像以及其它多维的信号来说，我们也需要滤波器。一般来说，任意二维函数都能成为一个二维滤波器，这样定义他们是有用的。不过在很多情况下，我们能从一维滤波器构造出合适的二维滤波器。最有用的方法就是使用一个可分离的滤波器（Separable Filter），对于一个可分离的滤波器\(f_2\)我们能得到

\[f_2(x,y) = f_1(x) f_1(y) \]

对于离散的滤波器可以得到

\[b_2[i,j] = b_1[i] b_1[j] \]

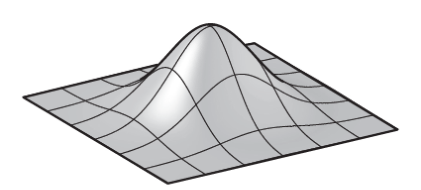
如果\(f_1\)为帐篷函数那么可以得到一个双线性分段函数\(f_2\)

\[f_{2,\mathrm{tent}}(x,y) = \begin{cases} (1-|x|)(1-|y|),|x|<1且|y|<1 \\ 0,其它情况 \end{cases} \]

下方为这个函数的示意图

如果我们让\(f_1\)为高斯函数那么能得到

\[\begin{align*} f_{2,g}(x,y) &= \frac{1}{2\pi} (e^{-x^2/2}e^{-y^2/2}) \\ &= \frac{1}{2\pi} (e^{-(x^2+y^2)/2}) \\ &= \frac{1}{2\pi} e^{-r^2/2} \end{align*} \]

下方为这个函数的示意图

  可分离的滤波器有个美妙的地方，这也是它在效率上优于别的二维滤波器的原因。让我们从离散卷积开始

\[(a \star b_2)[i,j] = \sum_{i^\prime} \sum_{j^\prime} a[i^\prime,j^\prime] b_1[i-i^\prime] b_1[j-j^\prime] \]

仔细观察可以发现最里面的一层求和为

\[\sum_{j^\prime} a[i^\prime,j^\prime] b_1[i-i^\prime] b_1[j-j^\prime] \]

相对于这一层求和来说\(b_1[i-i^\prime]\)是个常量，因此完全可以把它提取到外面一层的求和，于是卷积公式就变成了

\[(a \star b_2)[i,j] = \sum_{i^\prime} b_1[i-i^\prime] \sum_{j^\prime} a[i^\prime,j^\prime] b_1[j-j^\prime] \]

如果让\(i\)为横坐标，\(j\)为纵坐标，这个时候就发现了\((a \star b_2)[i,j]\)实际上是一纵列的求和乘以一个因子加上另一纵列的求和乘以另一个因子，一直到求和完毕。此外我们还能发现不管是\((a \star b_2)[i+1,j]\)还是\((a \star b_2)[i+2,j]\)，只要\(|k|\)小于等于滤波器的半径，\((a \star b_2)[i+k,j]\)的计算和\((a \star b_2)[i,j]\)的计算都会用到一些相同的纵列求和的结果，下方是一张形象的用来理解的图

假如我们要做下面这种类型的大规模计算

for(uint i=0;i<width;i++)
    for(uint j=0;j<height;j++)
        image[i,j] = Convolution(a,b,i,j)

这个时候你可能立马就想到了，我们可以复用纵列求和的结果，即先进行一次竖直方向上的卷积，计算出中间值也就是所有的位置纵列求和的结果，有了中间值后只要再进行一次水平方向上的卷积，即可完成整个卷积过程。这样计算就使时间复杂度从\(O(r^2)\)降到了\(O(r)\)，堪称完美！下面给出实现这个想法的伪代码

图像信号处理（Signal Processing for Image）

  目前我们已经以抽象的方式讨论过采样、滤波、重建，而且使用的大多数都是一维信号的例子。在计算机图形学中许多信号处理的重要应用都是应用于采样后的图像的，接下来让我们看看究竟是如何应用的。

使用离散滤波器滤波图像（Image Filtering Using Discrete Filters）

  也许卷积的最简单的应用就是使用离散卷积处理图像，那些在程序中被广泛使用的图像处理功能使用的都是简单的卷积滤波器，模糊图像可以通过使用许多常见的低通滤波器做到，从方框滤波器到高斯滤波器。一个高斯滤波器可以产生非常平滑的模糊，因此它被常用于模糊。下方是使用不同滤波器进行模糊的示例图

  与模糊相反的就是锐化，有一种能做到这样的方法是使用“反锐化蒙版”过程，就是减去模糊后图像的一部分，减去一部分后还要防止整体的亮度变化，用公式描述为

\[\begin{align*} I_{sharp} &= (1 + \alpha)I - \alpha(I \star f_{g,\sigma}) \\ &=I \star ((1+\alpha)d-\alpha f_{g,\sigma}) \\ &=I \star f_\mathrm{sharp}(\sigma,\alpha) \end{align*} \]

其中\(f_{g,\sigma}\)指代的是一个有着宽度\(\sigma\)的高斯滤波器，通过修改\(\sigma\)和\(\alpha\)我们就能获得不同程度的锐化效果，下方是一个示例图

  另一个结合两种离散滤波器的例子是投射阴影，可以通过模糊偏移后的物体轮廓做到，首先可以通过与离心的脉冲卷积完成偏移操作

\[d_{m,n}(i,j) = \begin{cases} 1,i=m且j=n \\ 0,其它情况 \end{cases} \]

偏移后接着再模糊，可以得到公式为

\[\begin{align*} I_\mathrm{shadow} &= (I \star d_{m,n}) \star f_{g,\sigma} \\ &= I \star (d_{m,n} \star f_{g,\sigma}) \\ &= I \star f_\mathrm{shadow}(m,n,\sigma) \end{align*} \]

下方是一张投射阴影的示例图

图像采样中的抗走样（Antialiasing in Image Sampling）

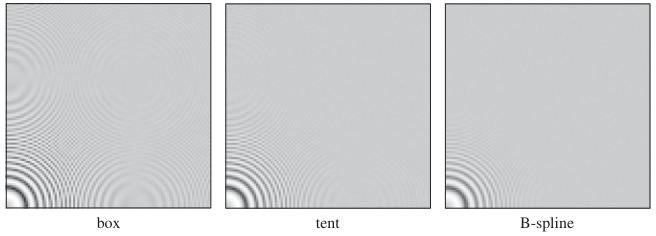
  在图像合成中，我们通常可以用公式计算出图像在任意一点的颜色，不过我们一般需要图像的采样表示，比如光线追踪就是个例子。以信号处理的语言来说，就是我们有一个连续的二维信号（图像），需要在一个规则的二维晶格上进行采样。如果不做任何特殊处理就采样图像，结果会出现各种各样的走样伪影。下面是一张示例图

  上图展示了位于锐利边缘处的台阶伪影也就是“锯齿”，此外在一些有重复图案的地方我们还能发现一些被称为摩尔纹的宽条纹。这里的问题其实是图像包含了很多小尺度细节，我们需要在采样前进行滤波，来让结果更平滑。一个简单的滤波器例如方框滤波器可以改善在锐利边缘处的表现，但是还是会产生一些摩尔纹。对于非常平滑的高斯滤波器来说，它在抗摩尔纹方面则有效得多，但是会造成一些模糊。这两个例子展示了，在锐度和走样之间进行衡量是选择抗走样滤波器的基础。下方的图像展示了使用不同滤波器进行采样的效果

重建和重采样（Reconstruction and Resampling）

  最常见之一的图像操作是重采样（Resampling），即改变采样率或改变图像大小。假设用一个有着3000x2000分辨率的数字相机拍了张图像，但是我们要在一个1280x1024的监视器上显示图像。为了让图像在保持\(3:2\)的比例下被显示，我们需要重采样到1278x852的分辨率。但是该怎么做呢？一个能做到这个的方法为抛弃像素，在图像中我们可以距离一定间隔地抛弃像素。这么做虽然速度很快，但是会导致处理后的图像的质量很差。
  调整图像大小的方法可以被看作是重采样操作，我们想要在一个新的维度获取表示相同图像的一系列样本，可以通过采样从原始样本重建后的连续函数做到。这样来看，实际上就是一系列的标准图像处理操作，首先我们从表示图像的原始样本重建一个连续函数，接着对这个连续函数进行采样。为了避免走样伪影，每个阶段应该用合适的滤波器。
  为了知道算法的细节，最好降到一维来讨论。下方为极简的重采样一维序列的代码

参数\(x_0\)为第一个样本的位置，通过\(x_0+i\Delta x\)我们就能知道后续样本的位置。像这样重建后直接进行点采样还不太对，因为重建后的连续函数可能有非常多的小尺度细节，因此还需要使用一个合适的采样滤波器\(g\)，让它与重建后的连续函数卷积，从而得到一个平滑化的连续函数\(g \star (f \star a)\)，最后再进行点采样就行。此外由卷积的性质可以得到\((g \star f) \star a=g \star (f \star a)\) ,因此重采样操作变成了点采样\((g \star f) \star a\)。下方是一张形象的重采样示例图

最后一个要解决的问题是如何处理在边界的情况，你可能也发现了一开始提供的代码会造成越界读取。下面有几个方法

1. 直接停下，等价于使用\(0\)填充超出边界的那部分。

2. 把读取位置重定向到边界位置，如果要读取\(a[-1]\)那么就返回\(a[0]\)，这等价于使用边界的值填充超出边界的那部分。

3. 当接近边界时修改滤波器，这样就不会越界读取。

第一个方法会导致重采样后的图像有暗淡的边缘，第二个方法很容易实现，第三个方法可能是表现最好的。
  选择用于重采样的滤波器很重要。有两个分开的问题，一个是滤波器的形状，另一个是滤波器的大小（半径）。因为要选择的滤波器会同时作为重建滤波器和采样滤波器，对两种滤波器的需求影响着如何选择滤波器。对于重建来说，我们想让滤波器足够平滑，避免放大图像时产生的走样伪影，此外滤波器还应该是无波纹的。对于采样来说，滤波器应该足够大来避免欠采样以及足够平滑来避免摩尔纹。下方的图像展示了这两种不同的需求

  一般来说，我们会选择一个滤波器的形状，然后根据输入和输出的相对分辨率来缩放。两个中更低的分辨率决定了滤波器的大小，当输出的分辨率比输入的分辨率小时，对于采样需要的平滑就高于对于重建需要的平滑，这个时候滤波器的大小就取决于输出样本的间距。当重建所需要的光滑占主导地位时，滤波器的大小取决于输入样本的间距。
 选择滤波器得在速度和质量之间进行衡量，常见的选择是方框滤波器（速度优先）、帐篷滤波器（中等质量）、三次分段滤波器（高质量）。当选择三次分段滤波器时，平滑度可以通过在\(f_{B}\)和\(f_{C}\)之间进行插值来调整，比如Mitchell-Netravali滤波器就是个好主意。
  在图像滤波中，可分离的滤波器能提供非常显著的速度提升，基本想法是先重采样所有行，产生一个宽度改变但高度不变的图像，接着再重采样所有列，这样就得到了最终结果。下方是一张形象的示例图

采样理论（Sampling Theory）

  学复变函数的时候老师根本没教这里的东西，这部分后面的内容都没太看懂。可能是我太菜了，应该得很久之后补上了😅。