国庆期间做题记录

好摆好摆，几天就写了几个题。

QOJ 网络赛题

记一辈子的题。

Xor Mirror

题意如下：

维护一个长为 \(n\) 的序列 \(A\)，支持两种操作：

输入 \(1,l,r,k\)，令 \(B_i=A_{i\oplus k}\space i\in[l,r)\)，再令 \(A_i=B_i\space i\in[l,r)\)。
输入 \(2,l,r\)，输出 \(\sum_{i=l}^{r-1}A_i\)。

保证 \(n=2^k-1\),\(k\in[1,18]\)。

题解：

操作非常阴间。

异或出来的数肯定是一段又一段的，所以不考虑线段树了，考虑分块。

如果按 \(\sqrt n\) 分块又显得不太好，因为还是碎碎的。

所以考虑按 \(i\) 的二进制值域高低位分块。

具体而言，把 \(i\) 拆成二进制，然后高九位和低九位分开。

同时将 \(k\) 拆成二进制，高九位低九位也分开。

发现，高九位相同的会被挪到一起，低九位相同的可以暴力挪。

那么修改整块就是直接一个指针挪过去。

修改散块需要重构，但是重构后原来的指针就完蛋了，所以要新建一个块再重构。

但是空间就起飞了，所以我们还需要内存回收。

大致过程如下，橙色表示修改的区间。

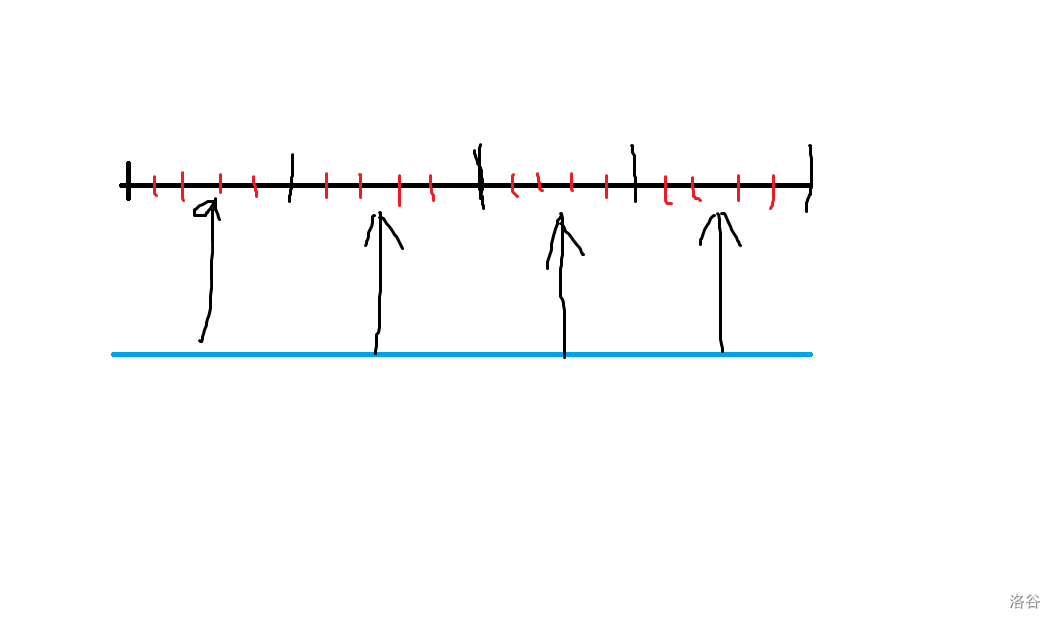
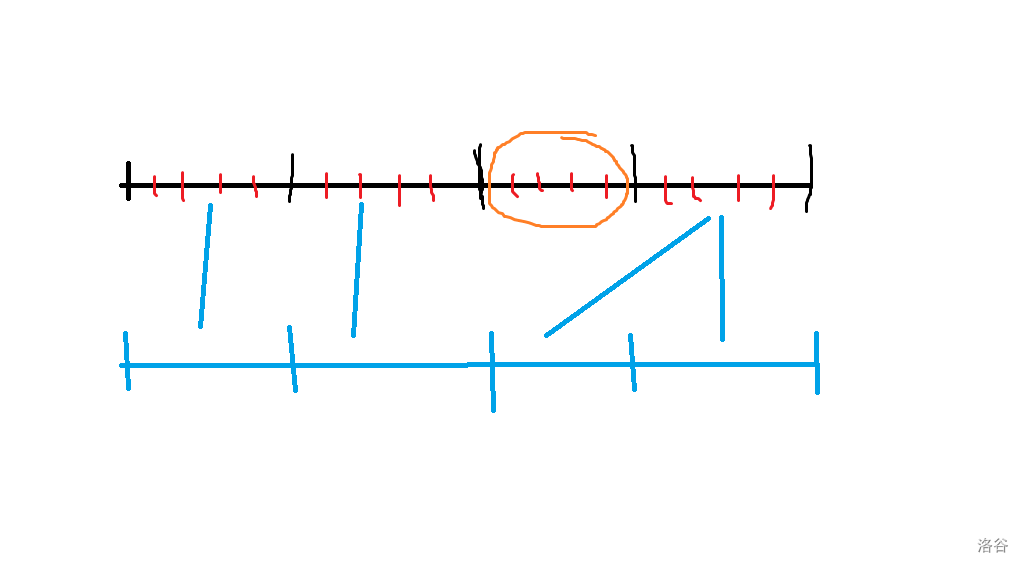
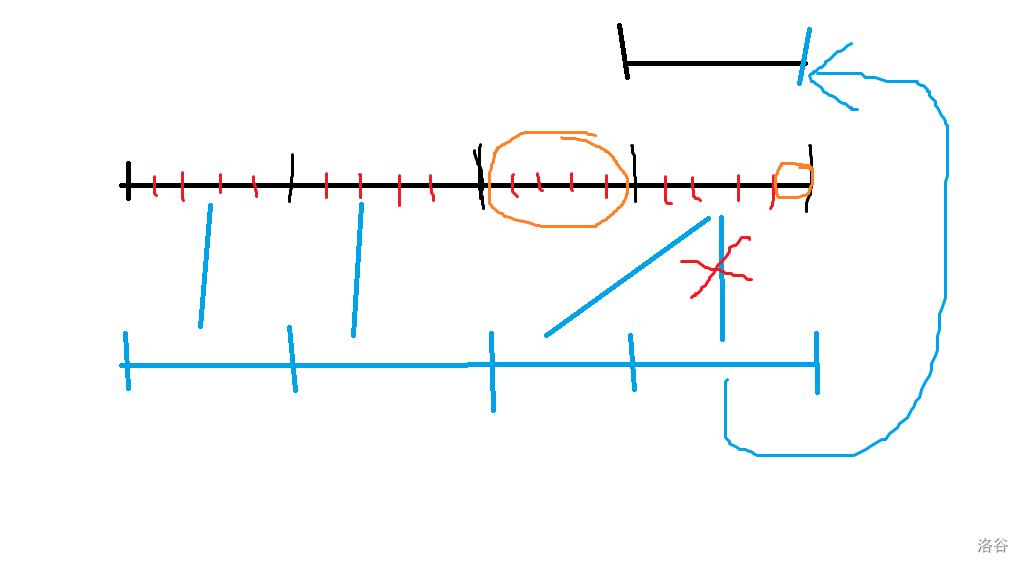
非常的抽象是吧，接下来看代码更抽象。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = (1<<18)+5;
int T,n,q;
vector<int> a[N];
ll sum[605];
int to[605],tag[605];
int pos1,pos2,vis[605];
int X,Y,B;
void newnode(){
	pos1=pos2=-1;
	for(int i=0;i<X;i++){
		if(vis[i]==0){
			if(pos1==-1) pos1=i;
			else if(pos2==-1) pos2=i;
			else return ;
		}
	}
}
void modify(int l,int r,int k){
	int lx=l/B,ly=l%B,rx=r/B,ry=r%B,kx=k/B,ky=k%B;
	if(lx==rx){
		vis[to[lx]]--;
		ll s=0;vector<int> vec;
		for(int j=0;j<Y;j++){
			if(j<ly || j>ry){
				vec.push_back(a[to[lx]][j^tag[lx]]);
			}else{
				vec.push_back(a[to[lx^kx]][j^tag[lx^kx]^ky]);
			}
			s+=vec[j];
		}
		newnode();
		to[lx]=pos1,tag[lx]=0,vis[pos1]++;
		a[pos1]=vec;sum[pos1]=s;
	}else{
		vis[to[lx]]--,vis[to[rx]]--;
		ll s1=0,s2=0;
		vector<int> v1,v2;
		for(int j=0;j<Y;j++){
			if(j<ly){
				v1.push_back(a[to[lx]][j^tag[lx]]);
			}else{
				v1.push_back(a[to[lx^kx]][j^tag[lx^kx]^ky]);
			}
			s1+=v1[j];
		}
		for(int j=0;j<Y;j++){
			if(j>ry){
				v2.push_back(a[to[rx]][j^tag[rx]]);
			}else{
				v2.push_back(a[to[rx^kx]][j^tag[rx^kx]^ky]);
			}
			s2+=v2[j];
		}
		if(rx-lx>1){
			vector<int> tmp,tmp2;
			for(int i=0;i<X;i++){tmp2.push_back(tag[i]);;tmp.push_back(to[i]);}
			for(int i=lx+1;i<=rx-1;i++){
				vis[to[i]]--;vis[tmp[i^kx]]++;
				to[i]=tmp[i^kx];tag[i]=tmp2[i^kx]^ky;
			}
		}
		newnode();
		to[lx]=pos1,tag[lx]=0,vis[pos1]++;a[pos1]=v1;sum[pos1]=s1;
		to[rx]=pos2,tag[rx]=0,vis[pos2]++;a[pos2]=v2;sum[pos2]=s2;
	}
}
ll query(int l,int r){
	int lx=l/B,ly=l%B,rx=r/B,ry=r%B;
	ll res=0;
	if(lx==rx){
		for(int j=ly;j<=ry;j++){
			res+=a[to[lx]][j^tag[lx]];
		}
	}else{
		for(int j=ly;j<Y;j++){
			res+=a[to[lx]][j^tag[lx]];
		}
		for(int i=lx+1;i<=rx-1;i++){
			res+=sum[to[i]];
		}
		for(int j=0;j<=ry;j++){
			res+=a[to[rx]][j^tag[rx]];
		}
	}
	return res;
}
void get(){
	int p=0;
	while((1<<p)<n) p++;
	int bn=(p+1)/2;
	B=(1<<bn);
	X=n/B,Y=B;
}
void solve(){
	cin>>n>>q;
	get();
	for(int i=0;i<X;i++) a[i].clear();
	for(int i=0;i<X;i++) sum[i]=tag[i]=0,to[i]=i,vis[i]=1;
	for(int i=0;i<X;i++){
		vector<int> vec;
		for(int j=0,x;j<Y;j++){
			cin>>x;
			vec.push_back(x);sum[i]+=x;
		}
		a[i]=vec;
	}
	for(int i=1,op,l,r;i<=q;i++){
		cin>>op>>l>>r;r--;
		if(op==1){
			int k;cin>>k;
			modify(l,r,k);
		}else{
			cout << query(l,r) << '\n';
		}
	}
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

AtCoder

AT 没有提交记录查看，这非常不好，只能找近几场的赛题了。

Clearance

题意如下：

维护一个序列，支持一个操作：

\(l,r,k\) 表示在 \(l,r\) 区间中每个位置取 \(min(k,A_i)\) 个物品，并 \(A_i=max(A_i-k,0)\)。

题解

势能分析线段树。

以区间 \(min\) 为势能，如果区间 \(min\) 小于 \(k\) 就一直递归，否则打标记返回 \(k\times cnt_u\)。

如果出现了一个 \(0\)，那么将其的 \(cnt\) 设置为 \(0\)，将 \(A_i\) 设置为 \(inf\)。

以及如果一个区间里 \(min\) 全为 \(0\) 则提前返回 \(0\)。

证明：

如果区间 \(min\) 一直不为 \(0\)，就是普通线段树。
如果有一个节点为 \(0\)，将其设为 \(inf\)，最多会有 \(n\) 次递归到叶子。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N = 3e5+10;
constexpr ll inf = 1e16;
int n,q;
ll a[N];
struct SegTree{
#define ls u<<1
#define rs u<<1|1
#define mid ((l+r)>>1)
	ll tag[N<<2],mn[N<<2];
	int cnt[N<<2];
	void pushup(int u){
		mn[u]=min(mn[ls],mn[rs]);
		cnt[u]=cnt[ls]+cnt[rs];
	}
	void build(int u,int l,int r){
		if(l==r){
			mn[u]=a[l];
			tag[u]=0;cnt[u]=1;
			return ;
		}
		build(ls,l,mid);build(rs,mid+1,r);
		pushup(u);
	}
	void upd(int u,ll k){
		mn[u]+=k;tag[u]+=k;
		if(mn[u]<=0){
			cnt[u]=0;mn[u]=inf;
		}
	}
	void pushdown(int u){
		if(!tag[u]) return ;
		if(mn[ls]!=inf) upd(ls,tag[u]);
		if(mn[rs]!=inf) upd(rs,tag[u]);
		tag[u]=0;
	}
	ll query(int u,int l,int r,int x,int y,ll k){
		if(mn[u]==inf) return 0;
		if(l==r && mn[u]<=k){
			ll res=mn[u];
			mn[u]=inf;cnt[u]=0;
			return res;
		}
		if(l>=x && r<=y){
			if(mn[u]>k){
				mn[u]-=k;tag[u]-=k;
				return k*1ll*cnt[u];
			}else{
				ll res=0;
				pushdown(u);
				if(x<=mid) res+=query(ls,l,mid,x,y,k);
				if(mid<y) res+=query(rs,mid+1,r,x,y,k);
				pushup(u);
				return res;
			}
		}
		ll res=0;pushdown(u);
		if(x<=mid) res+=query(ls,l,mid,x,y,k);
		if(mid<y) res+=query(rs,mid+1,r,x,y,k);
		pushup(u);
		return res;
	}
}T;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	T.build(1,1,n);
	cin>>q;
	for(int i=1,l,r;i<=q;i++){
		ll k;cin>>l>>r>>k;
		cout << T.query(1,1,n,l,r,k) << '\n';
	}
	return 0;
}

Range Shuffle Query

题意如下：

给你一个长度为 \(N\) 的序列 \(A = (A_1, A_2, \dots, A_N)\) 。

处理 \(Q\) 个查询。

每个查询都给出了整数 \(L\), \(R\), \(X\) 并要求你解决以下问题。

假设 \(B = (A_L,A_{L+1}, \dots, A_R)\) 是由 \(A\) 的 \(L\) 到 \(R\) 元素组成的序列。

执行下面的程序一次：

首先，从 \(B\) 中删除每个值至少为 \(X\) 的元素。

然后，任意重新排列 \(B\) 的其余元素。

可以得到多少个不同的序列 \(B\) ？并对 \(998244353\) 的模数。

题解：

有可重集的排列数 \(\dfrac{n!}{n_1!n_2!\dots n_k!}\)

然后上面的 \(n\) 直接莫队+值域分块，下面的依托显然可以在莫队移动时 \(O(1)\) 维护。

因为取模的性质烂到家了，所以用最保守的维护方式：先把贡献全清了再加回去。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define B 500
#define L(i) ((i-1)*B+1)
#define R(i) min(i*B,n)
#define bel(i) ((i-1)/B+1)
using namespace std;
constexpr int N = 3e5+10;
constexpr int p = 998244353;
ll qpow(ll a,ll b){
	ll res=1;
	while(b){
		if(b&1) res=res*a%p;
		b>>=1;a=a*a%p;
	}
	return res%p;
}
int n,m;
ll a[N];
struct Q{
	int l,r,x,id;
	bool operator < (const Q &a)const{
		return (l/B==a.l/B) ? (l/B)&1 ? r<a.r : r>a.r : l<a.l; 
	}
}q[N];
int l=1,r=0;
ll fac[N],ans[N],inv[N];
ll cnt[N],mul[N],sum[N];
void add(int x){
	mul[bel(x)]=mul[bel(x)]*fac[cnt[x]]%p;
	cnt[x]++;
	sum[bel(x)]++;
	mul[bel(x)]=mul[bel(x)]*inv[cnt[x]]%p;
}
void del(int x){
	mul[bel(x)]=mul[bel(x)]*fac[cnt[x]]%p;
	cnt[x]--;
	sum[bel(x)]--;
	mul[bel(x)]=mul[bel(x)]*inv[cnt[x]]%p;	
}
ll query(int x){
	ll res1=0,res2=1;
	for(int i=1;i<bel(x);i++){
		res1=(res1+sum[i])%p;
		res2=res2*mul[i]%p;
	}
	for(int j=L(bel(x));j<x;j++){
		res1=(res1+cnt[j])%p;
		res2=res2*inv[cnt[j]]%p;
	}
	return fac[res1]*res2%p;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	fac[0]=1;for(int i=1;i<N;i++) fac[i]=fac[i-1]*i%p,mul[i]=1;
	inv[0]=1;for(int i=1;i<N;i++) inv[i]=qpow(fac[i],p-2);
	cin>>n>>m;
	for(int i=1;i<=n;i++){cin>>a[i];}
	for(int i=1;i<=m;i++){
		cin>>q[i].l>>q[i].r>>q[i].x;
		q[i].id=i;
	}
	sort(q+1,q+1+m);
	for(int i=1;i<=m;i++){
		while(l>q[i].l) add(a[--l]);
		while(r<q[i].r) add(a[++r]);
		while(l<q[i].l) del(a[l++]);
		while(r>q[i].r) del(a[r--]);
		ans[q[i].id]=query(q[i].x);
	}
	for(int i=1;i<=m;i++){cout << ans[i] << '\n';}
	return 0;
}

Luogu

狼坑 Trous de loup

如果不修改，显然可以双指针直接做。

修改就相当于是有一定的容错，可以再套一个双指针，表示删去的最大区间的数。

转移可以用单调队列优化。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N = 2e6+10;
int n,d,ans;
ll m,a[N],arr[N];
int head,tail,que[N],l;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>d;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		arr[i]=arr[i-1]+a[i];
	}
	ans=d,que[tail]=d,l=1;
	for(int i=d+1;i<=n;i++){
		while(head<=tail && arr[i]-arr[i-d]>arr[que[tail]]-arr[que[tail]-d]) tail--;
		que[++tail]=i;
		while(head<=tail && arr[i]-arr[l-1]-arr[que[head]]+arr[que[head]-d]>m){
			l++;
			while(head<=tail && que[head]-d+1<l) head++;
		}
		ans=max(ans,i-l+1);
	}
	cout << ans << '\n';
	return 0;
}

一步最优

题意如下：

给出一个序列。

贪心选择序列中的子段和最大的子段，所有子段不能有交，最多选择 \(m\) 段。

回答该算法在 \(m\in [1,n]\) 时能得到所有子段和之和的最大值与最小值。

题解：

发现出现差距的操作是子段和相同时，选择了哪一段。

自然的发现，想让子段和最大，我们需要选择子段长度最小的那一段。

证明：

考虑两段不交，那就两段都能选。
考虑两段包含，选短的可以给其它选择留下更多的数。
考虑两段有交但不包含，因为最大子段和中任意一段前后缀和都大于等于 \(0\)（如果前后缀和小于 \(0\)，那么可以直接扔掉。），所以易得两段可以直接合并，不存在。

反之亦然。

线段树动态维护区间最大子段和和区间赋值操作。

其中区间赋值只需要赋极小值，可以直接暴力做。

证明：

因为题目要求选择的子段数不超过 \(m\)，所以子段和的最大值最小为 \(0\)。当全局都小于 \(0\) 的时候就可以跳过了。总计操作 \(O(n)\) 次。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define inf 1e14
using namespace std;
constexpr int N = 2e5+10;
int T,n,a[N];
struct node{
	ll val;int l,r;
};
node MX(bool t,const node &x,const node &y){
	if(x.val==y.val) return x.r-x.l<y.r-y.l ? (t==1?x:y) : (t==1?y:x);
	return x.val>y.val ? x : y;
}
struct Tree{
	ll v;int l,r;
	node mx,lmx,rmx;
}tr[N<<2][2];
Tree merge(bool t,const Tree &x,const Tree &y){
	Tree res={0,0,0};
	res.v=x.v+y.v;
	res.lmx=MX(t,x.lmx,(node){x.v+y.lmx.val,x.l,y.lmx.r});
	res.rmx=MX(t,y.rmx,(node){y.v+x.rmx.val,x.rmx.l,y.r});
	res.mx=MX(t,MX(t,x.mx,y.mx),(node){x.rmx.val+y.lmx.val,x.rmx.l,y.lmx.r});
	res.l=x.l,res.r=y.r;
	return res;
}
struct SegTree{
#define ls u<<1
#define rs u<<1|1
#define mid ((l+r)>>1)
	void pushup(int u,bool t){tr[u][t]=merge(t,tr[ls][t],tr[rs][t]);}
	void upd(int u,ll k,bool t){tr[u][t].v=tr[u][t].lmx.val=tr[u][t].rmx.val=tr[u][t].mx.val=k;}
	void init(int u,int id,int k,bool t){tr[u][t].v=k,tr[u][t].lmx=tr[u][t].rmx=tr[u][t].mx={k,id,id};}
	void build(bool t,int u=1,int l=1,int r=n){
		tr[u][t].l=l,tr[u][t].r=r;
		if(l==r){init(u,l,a[l],t);return;}
		build(t,ls,l,mid);build(t,rs,mid+1,r);
		pushup(u,t);
	}
	void modify(int x,ll k,bool t,int u=1,int l=1,int r=n){
		if(l==r){upd(u,k,t);return ;}
		if(x<=mid) modify(x,k,t,ls,l,mid);
		else modify(x,k,t,rs,mid+1,r);
		pushup(u,t);
	}
}Tr;
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	Tr.build(1);Tr.build(0);
	ll ans=0;
	for(int t=1;t>=0;t--){
		for(int i=1;i<=n;i++){
			node res=tr[1][t].mx;
			if(res.val>0){
				ans+=res.val;
				for(int j=res.l;j<=res.r;j++) Tr.modify(j,-inf,t);
			}
			cout << ans << ' ';
		}
		ans=0;cout << '\n';
	}
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

[Ynoi2005] rmscne

题解：

显然有 \(O(nq)\) 的双指针做法。

但是这玩意没法优化，所以我们换一个。

考虑扫描线，对 \(r\) 升序排序，每次维护 \(l\) 找到一个 \(r'\) 使得 \(r'\) 最小且符合条件。

然后对 \(r\) 求一个最大的 \(l'\) 且符合条件。

那么答案就在 \(l',r'\) 之间，然后对其求 \(r'-i\) 的最小值即可。

用并查集维护。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N = 2e6+10;
struct SegTree{
#define ls (u<<1)
#define rs (u<<1|1)
#define mid ((l+r)>>1)
	int tr[N<<2],tag[N<<2];
	void pushup(int u){tr[u]=min(tr[ls],tr[rs]);}
	void upd(int u,int r,int c){tr[u]=c-r+1;tag[u]=c;}
	void pushdown(int u,int l,int r){
		if(tag[u]==-1) return ;
		upd(ls,mid,tag[u]);upd(rs,r,tag[u]);
		tag[u]=-1;
	}
	void build(int u,int l,int r){
		tag[u]=-1;if(l==r) return ;
		build(ls,l,mid);build(rs,mid+1,r);
	}
	void modify(int u,int l,int r,int x,int y,int c){
		if(l>=x && r<=y){upd(u,r,c);return ;}
		pushdown(u,l,r);
		if(x<=mid) modify(ls,l,mid,x,y,c);
		if(mid<y) modify(rs,mid+1,r,x,y,c);
		pushup(u);
	}
	int query(int u,int l,int r,int x,int y){
		if(l>=x && r<=y) return tr[u];
		int res=2e9;pushdown(u,l,r);
		if(x<=mid) res=min(res,query(ls,l,mid,x,y));
		if(mid<y) res=min(res,query(rs,mid+1,r,x,y));
		return res;
	}
}T;
int n,a[N],m;
struct Q{int l,id;};
vector<Q> q[N];
int fa[N],lst[N],ans[N];
int find(int x){return fa[x]==x ? x : fa[x]=find(fa[x]);}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=0;i<=n;i++) fa[i]=i;
	cin>>m;
	for(int i=1,l,r;i<=m;i++){
		cin>>l>>r;
		q[r].push_back({l,i});
	}
	T.build(1,1,n);
	for(int i=1;i<=n;i++){
		T.modify(1,1,n,lst[a[i]]+1,i,i);
		if(lst[a[i]]) fa[lst[a[i]]]=lst[a[i]]+1;
		lst[a[i]]=i;
		for(auto x:q[i]){
			int l=x.l,r=find(l),id=x.id;
			ans[id]=T.query(1,1,n,l,r);
		}
	}
	for(int i=1;i<=m;i++){
		cout << ans[i] << '\n';
	}
	return 0;
}

Codeforces

Multiples and Power Differences

题解：

如果没有第三个要求，直接输出 \(lcm(1,2,\dots,16)\)，也就是 \(720720\)。

然后我们修一下这个即可，给方格图黑白染色，\(i+j\) 为偶数的染白，否则染黑。

所有黑点加上 \(a_{i,j}^4\) 即可。

点击查看代码

#include<bits/stdc++.h>

using namespace std;
constexpr int N = 510;
int n,m;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			int x;cin>>x;
			if((i+j)&1) cout << 720720<<' ';
			else{
				cout << 720720+x*x*x*x<<' ';
			}
		}cout << '\n';
	}
	return 0;
}

Kefa and Watch

题解：

观察到，判断是否存在长度为 \(k\) 的周期，可以 check \(l\to r-k\) 与 \(l+k\to r\) 是否相等。

然后用线段树维护 hash 值即可。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N = 1e5+10;
constexpr int base=17;
constexpr int p = 1e9+9;
int n,m,k;ll pw[N],pw2[N];
ll d[N],a[N];
string s;
struct SegTree{
#define ls (u<<1)
#define rs (u<<1|1)
#define mid ((l+r)>>1)
	ll tr[N<<2],len,tag[N<<2];
	void pushup(int u,int l,int r){
		tr[u]=(tr[ls]*pw[r-mid]%p+tr[rs]+p)%p;
	}
	void build(int u,int l,int r){
		tag[u]=-1;
		if(l==r){tr[u]=a[l];return ;}
		build(ls,l,mid);build(rs,mid+1,r);
		pushup(u,l,r);
	}
	void upd(int u,int c,int len){
		tag[u]=c;tr[u]=(pw2[len-1]*c%p+p)%p;
	}
	void pushdown(int u,int l,int r){
		if(tag[u]==-1) return ;
		upd(ls,tag[u],mid-l+1);
		upd(rs,tag[u],r-mid);
		tag[u]=-1;
	}
	void modify(int u,int l,int r,int x,int y,int c){
		if(l>=x && r<=y){upd(u,c,r-l+1);return ;}
		pushdown(u,l,r);
		if(x<=mid) modify(ls,l,mid,x,y,c);
		if(mid<y) modify(rs,mid+1,r,x,y,c);
		pushup(u,l,r);
	}
	ll query(int u,int l,int r,int x,int y){
		if(l>=x && r<=y){return tr[u]%p;}
		pushdown(u,l,r);
		ll res=0;
		if(x<=mid) res=query(ls,l,mid,x,y);
		if(mid<y) res=(res*pw[min(r,y)-mid]+query(rs,mid+1,r,x,y))%p;
		return res;
	}
}T;
mt19937 rnd(time(0));
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	pw[0]=pw2[0]=1;
	for(int i=1;i<N;i++) pw[i]=pw[i-1]*base%p;
	for(int i=1;i<N;i++) pw2[i]=(pw2[i-1]+pw[i])%p;
	cin>>n>>m>>k;
	cin>>s;s=' '+s;
	for(int i=0;i<=9;i++) d[i]=(rnd()+p)%p;
	for(int i=1;i<=n;i++){
		a[i]=(d[s[i]-'0']+p)%p;
	}
	T.build(1,1,n);
	for(int i=1,op,l,r,c;i<=m+k;i++){
		cin>>op>>l>>r>>c;
		if(op==1){
			c=d[c];
			T.modify(1,1,n,l,r,c);
		}else{
			if(c==r-l+1) cout << "YES\n";
			else if(T.query(1,1,n,l,r-c)==T.query(1,1,n,l+c,r)) cout << "YES\n";
			else cout << "NO\n";
		}
	}
	return 0;
}

Game of Slots

题解：

让保留 6 位小数，而值域是 \([1,1e18]\)。经过简单估算，可以发现出现两个值的概率很低，在保留小数的前提下基本不影响最后的答案，所以我们当任意两数都不同。

然后分析两者的放法。

先放的肯定贪心的从大到小依次放置，因为你能赢就是能赢，不能赢一定会输。

然后考虑后手的策略，一定是类田忌赛马，能赢就放能赢的最小的，不能赢就放全局最小的。

然后就把题目变成了一个计数问题了，一个 \(2n\) 的 01 串，共有 \(n\) 个 \(0\) 与 \(n\) 个 \(1\)。

对这个玩意求期望。

设 \(f_{i,j,k}\) 表示放了 \(i\) 个 \(0\)，\(j\) 个 \(1\)，还有 \(k\) 个 \(1\) 可用的情况下，先手的得分和。

然后记搜即可qwq。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N = 110;
int n;
double f[N][N][N];
double solve(int n,int m,int k){
	if(n<0 || m<0) return 0;
	if(n==0 && m==0) return 0;
	double &v=f[n][m][k];
	if(v!=-1) return v;
	double p=1.0*n/(n+m);
	v=p*solve(n-1,m,max(0,k-1))+(1.0-p)*solve(n,m-1,k+1);
	if(!k) v=v+p*n;
	return v;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	for(int i=0;i<N;i++)
		for(int j=0;j<N;j++)
			for(int k=0;k<N;k++)
				f[i][j][k]=-1;
	cin>>n;
	solve(n,n,0);
	cout << fixed<< setprecision(6)<<f[n][n][0];
	return 0;
}

Pudding Monsters

题意如下：

给定一个长为 \(n\) 的排列，问 \(l,r\) 重排后是否连续。

题解：

老题新做。

判断合法有 \(Max-Min=r-l\)。移项得到 \(Max-Min+l-r=0\)。

只需要维护这个组数就行了。但是等于 \(0\) 这个条件太强了，很难维护。

直接改成维护 \(Max-Min+l-r\) 的最小值与组数，然后等于 \(0\) 时返回组数否则返回 \(0\)。

对 \(r\) 扫描线，每次 \(r\) 增加的时候，上述式子会先 \(-1\)，全局减即可。

\(l\) 的贡献不变，开始时直接 build 进去就行。

\(Max,Min\) 同样的，这里讨论 \(Max\)。

维护一个递减的单调栈，如果 \(Max\) 被更新，就更新 \(sta_{top-1}+1\to sta_{top}\) 这个区间。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N = 5e5+10;
int n;
struct node{
	int x,y;
	bool operator < (const node &a){
		return x<a.x;
	}
}a[N],s1[N],s2[N];
int tp1,tp2;
ll ans=0;
struct SegTree{
#define ls (u<<1)
#define rs (u<<1|1)
#define mid ((l+r)>>1)
	int mn[N<<2];ll tag[N<<2],sum[N<<2];
	void pushup(int u){
		mn[u]=min(mn[ls],mn[rs]);sum[u]=0;
		if(mn[u]==mn[ls]) sum[u]+=sum[ls];
		if(mn[u]==mn[rs]) sum[u]+=sum[rs];
	}
	void build(int u,int l,int r){
		if(l==r){mn[u]=l;sum[u]=1;return ;}
		build(ls,l,mid);build(rs,mid+1,r);
		pushup(u);
	}
	void upd(int u,ll k){
		mn[u]+=k;tag[u]+=k;
	}
	void pushdown(int u){
		if(!tag[u]) return;
		upd(ls,tag[u]);upd(rs,tag[u]);
		tag[u]=0;
	}
	void modify(int u,int l,int r,int x,int y,ll k){
		if(l>=x && r<=y){upd(u,k);return;}
		pushdown(u);
		if(x<=mid) modify(ls,l,mid,x,y,k);
		if(mid<y) modify(rs,mid+1,r,x,y,k);
		pushup(u);
	}
	ll query(int u,int l,int r,int x,int y){
		if(l>=x && r<=y){return mn[u]==0 ? sum[u] : 0;}
		ll res=0;pushdown(u);
		if(x<=mid) res+=query(ls,l,mid,x,y);
		if(mid<y) res+=query(rs,mid+1,r,x,y);
		return res;
	}
}T;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){cin>>a[i].x>>a[i].y;}
	sort(a+1,a+1+n);
	T.build(1,1,n);
	for(int i=1;i<=n;i++){
		T.modify(1,1,n,1,n,-1);
		while(tp1 && s1[tp1].y<a[i].y){
			T.modify(1,1,n,s1[tp1-1].x+1,s1[tp1].x,a[i].y-s1[tp1].y);
			--tp1;
		}
		s1[++tp1]={i,a[i].y};
		while(tp2 && s2[tp2].y>a[i].y){
			T.modify(1,1,n,s2[tp2-1].x+1,s2[tp2].x,s2[tp2].y-a[i].y);
			--tp2;
		}
		s2[++tp2]={i,a[i].y};
		ans+=T.query(1,1,n,1,i);
	}
	cout << ans << '\n';
	return 0;
}

Weights

题解：

大麻题。

对砝码排序后分组，分成 \(0101010101\) 这类。

然后倒着做，假设此时天平向右倾斜。

如果想让天平向左倾斜，取掉最右侧的 \(1\)，变成 \(010101010\)。

如果想让天平向右倾斜，取掉最左侧的 \(0\)，变成 \(101010101\)。

然后奇数仿照上面的操作即可。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define m_p make_pair
using namespace std;
constexpr int N = 2e5+10;
int n,a[N],ans[N];
string s;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	cin>>s;s=' '+s;
	sort(a+1,a+1+n);
	for(int l=1,r=n;l<=r;){
		int len=r-l+1;
		ans[len]=(s[len]==s[len-1]?l++:r--);
	}
	for(int i=1;i<=n;i++){
		cout << a[ans[i]] << ' ' << ((ans[i]&1)^(n&1)^(s[n]=='R') ? 'R' : 'L') << '\n'; 
	}
	return 0;
}

posted @ 2025-10-11 21:26 Tighnari 阅读(9) 评论(0) 收藏举报

刷新页面返回顶部

QOJ 网络赛题

题意如下：

题解：

AtCoder

题意如下：

题解

题意如下：

题解：

Luogu

题解：

题解：

Codeforces

题解：

题解：

题解：

题意如下：

题解：

题解：

公告