2025.5.27-2025.5.28做题记录
前言
不想写 dp ,于是随便找找题做了。
题目
例题A:旅游巴士
CSP-J2023 某人人生的第一场 OI,打的是依托。
似乎是没学 dp,没学图论,没有做题技巧或者思维。
就学了点搜索。果然学竞赛不能跟着大众校外机构(tctm)啊。
也算认识到不少人了吧,出去集训还认识了现在在 cdqz 的朋友,虽然他好像不学 OI 了。
观察到 \(k\le 100\),考虑直接分层图。
如果我们到达某个点的时候,还没开门,我们可以直接加上 \(k\) 的正整数倍,然后到达。
然后直接上 dijkstra。没了。
点击查看代码
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int N=1e4+10;
const int M=2e4+10;
const int inf=0x3f3f3f3f;
int n,m,k;
struct node{
int v,a;
};
vector<node> vec[N];
int dis[N][110];
bool vis[N][110];
struct Dij{
int id,i,val;
bool operator <(const Dij x)const{
return val>x.val;
}
};
priority_queue<Dij> que;
void dij(){
que.push({1,0,0});
memset(dis,0x3f,sizeof(dis));
dis[1][0]=0;
while(!que.empty()){
Dij q=que.top();que.pop();
int u=q.id,i=q.i;
if(vis[u][i]) continue;
vis[u][i]=1;
for(node to:vec[u]){
int v=to.v,a=to.a;
int t=dis[u][i],w=(i+1)%k;
if(t<a) t+=(a-t+k-1)/k*k;
if(dis[v][w]>t+1){
dis[v][w]=t+1;
que.push({v,w,t+1});
}
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=1;i<=m;i++){
int u,v,a;
cin>>u>>v>>a;
vec[u].push_back({v,a});
}
dij();
if(dis[n][0]==inf) cout << -1;
else cout << dis[n][0];
return 0;
}
例题B:相连的边
注意到,题目中要求的三条边只能是菊花或者一条链!
我们直接考虑枚举花心,然后求出一个答案。
在枚举每条边的中间那条,再求出一个答案。
两个答案取 \(\max\) 就是最后答案。
难的可能是优美的代码实现:
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+10;
struct node{
int v;
ll val;
};
bool cmp(node a,node b){
return a.val>b.val;
}
vector<node> vec[N];
int n;
ll sum,ans;
int main(){
cin>>n;
for(int i=2;i<=n;i++){
int v,val;
cin>>v>>val;
vec[i].push_back({v,val});
vec[v].push_back({i,val});
}
for(int i=1;i<=n;i++){
sort(vec[i].begin(),vec[i].end(),cmp);
if(vec[i].size()<3) continue;
sum=vec[i][0].val+vec[i][1].val+vec[i][2].val;
ans=max(ans,sum);
}
for(int i=1;i<=n;i++){
if(vec[i].size()==1) continue;
for(node to:vec[i]){
int j=to.v,val=to.val;
if(vec[j].size()==1) continue;
sum=val;
sum+=(vec[j][0].v==i ? vec[j][1].val : vec[j][0].val);
sum+=(vec[i][0].v==j ? vec[i][1].val : vec[i][0].val);
ans=max(ans,sum);
}
}
cout << ans;
return 0;
}
例题C:小Z的袜子
莫队模板题,莫队就是暴力!
首先分块,把给出的序列分块,然后把询问按照分好的块左端点排序。
暴力求出第一个询问的答案,第二个询问答案直接通过移动指针完成。
时间复杂度被证明为 \(O(n\sqrt n)\)。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e4+10;
int n,m,len;
int c[N];
ll sum;
int cnt[N];
ll ans1[N],ans2[N];
struct Query{
int l,r,id;
}q[N];
bool cmp(Query a,Query b){
if(a.l/len==b.l/len) return ((a.l/len)&1) ? a.r<b.r : a.r>b.r;
return a.l<b.l;
}
//奇偶性排序优化
void add(int u){
sum+=cnt[u];
cnt[u]++;
}
void del(int u){
cnt[u]--;
sum-=cnt[u];
}
int main(){
cin>>n>>m;
len=sqrt(n);
for(int i=1;i<=n;i++){
cin>>c[i];
}
for(int i=1;i<=m;i++){
cin>>q[i].l>>q[i].r;
q[i].id=i;
}
sort(q+1,q+1+m,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){
if(q[i].l==q[i].r){
ans1[q[i].id]=0;
ans2[q[i].id]=1;
continue;
}
while(l>q[i].l) add(c[--l]);
while(r<q[i].r) add(c[++r]);
while(l<q[i].l) del(c[l++]);
while(r>q[i].r) del(c[r--]);
ans1[q[i].id]=sum;
ans2[q[i].id]=(ll)(r-l+1)*(r-l)/2;
}
for(int i=1;i<=m;i++){
if(ans1[i]!=0){
ll gcd=__gcd(ans1[i],ans2[i]);
ans1[i]/=gcd,ans2[i]/=gcd;
}else{
ans2[i]=1;
}
cout << ans1[i]<<'/'<<ans2[i]<<'\n';
}
return 0;
}
例题D:狼人游戏
草这怎么是树形 dp 。
从题目的限制中可以得到最后的保护与指控关系构成一棵树。
然后我们把树建出来,指控边为 1,保护边为 2。
套用树形背包定义 \(f_{i,j,0/1}\) 表示以 \(i\) 为根的子树,里面有 \(j\) 个狼人,\(i\) 是/不是 狼人。
然后套用背包的转移。
点击查看代码
#include<iostream>
#include<vector>
#define ll long long
using namespace std;
const int N=210;
const int p=1e9+7;
struct node{
int v,w;
};
vector<node> vec[N];
int f[N][N][2];
int n,w,m,in[N],siz[N];
void dfs(int u){
f[u][0][0]=1;
f[u][1][1]=1;
siz[u]=1;
for(auto to:vec[u]){
int v=to.v,w=to.w;
dfs(v);
siz[u]+=siz[v];
for(int i=siz[u];i>=0;i--){
ll tmp0=0,tmp1=0;
for(int j=min(i,siz[v]);j>=0;j--){
if(w){
tmp0=(tmp0+1ll*f[u][i-j][0]*(f[v][j][1]+f[v][j][0])%p)%p;
tmp1=(tmp1+1ll*f[u][i-j][1]*f[v][j][0])%p;
}else{
tmp0=(tmp0+1ll*f[u][i-j][0]*(f[v][j][1]+f[v][j][0])%p)%p;
tmp1=(tmp1+1ll*f[u][i-j][1]*f[v][j][1])%p;
}
}
f[u][i][0]=tmp0;
f[u][i][1]=tmp1;
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>w>>m;
for(int i=1;i<=m;i++){
char op;int a,b;
cin>>op>>a>>b;
if(op=='A'){
vec[a].push_back({b,1});
}else{
vec[a].push_back({b,0});
}
in[b]++;
}
for(int i=1;i<=n;i++){
if(in[i]==0){
vec[0].push_back({i,1});
}
}
dfs(0);
cout << f[0][w][0];
return 0;
}
例题E:【模板】三维偏序(陌上花开)
好好听的名字。
三维偏序怎么能少得了我高贵(暴力)的树套树呢!
一维排序,剩下两维用树状数组套权值线段树维护二维前缀和。
关于树套树维护二维前缀和,可以把它们放到坐标轴上,树状数组维护了 \(x\) 轴,权值线段树维护了 \(y\) 轴。
由树状数组先钦定 \(x\) 轴的范围,再由权值线段树去统计 \(y\) 轴上有多少个点。如图(有点乱):
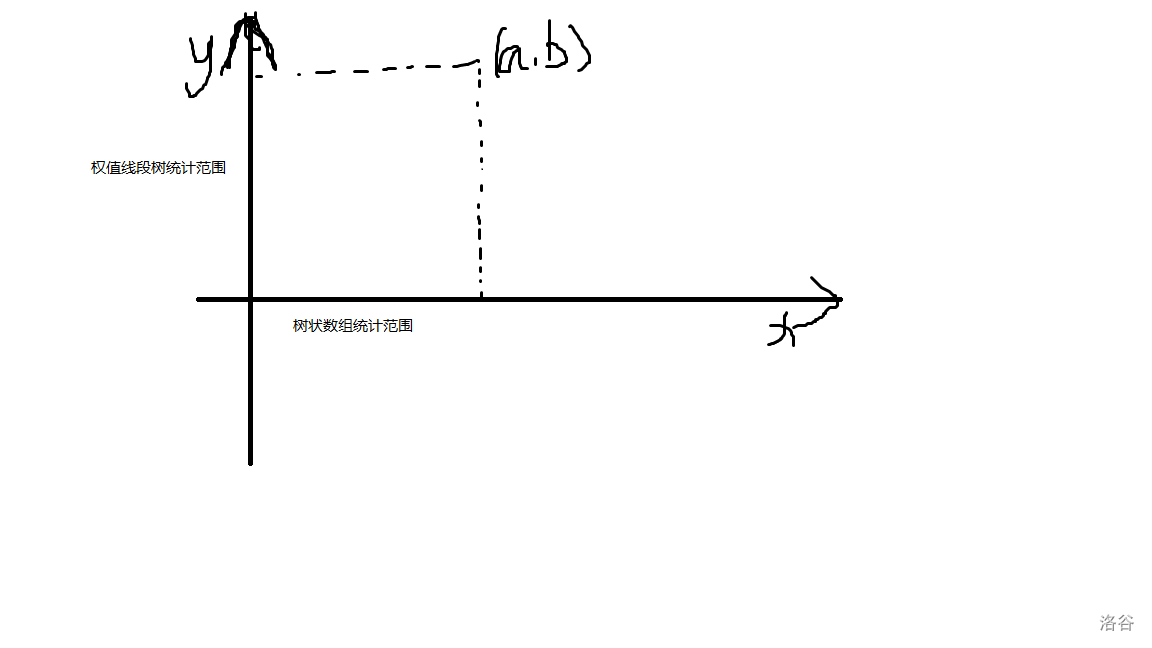
点击查看代码
#include<bits/stdc++.h>
#define lowbit(i) i&-i
using namespace std;
const int N=1e5+10;
const int K=2e5+10;
int n,k;
struct node{
int a,b,c;
}p[K];
bool cmp(node a,node b){
return a.a!=b.a ? a.a<b.a : (a.b!=b.b ? a.b<b.b : a.c<b.c);
}
struct Tree{
int val;
int ls,rs;
}tr[K<<6];
int tot,rt[K<<6];
void pushup(int u){
tr[u].val=tr[tr[u].ls].val+tr[tr[u].rs].val;
}
void modify(int &u,int l,int r,int x,int val){
if(!u) u=++tot;
if(l==r){
tr[u].val+=val;
return ;
}
int mid=(l+r)>>1;
if(x<=mid) modify(tr[u].ls,l,mid,x,val);
else modify(tr[u].rs,mid+1,r,x,val);
pushup(u);
}
int query(int u,int l,int r,int x,int y){
if(!u) return 0;
if(l>=x && r<=y){
return tr[u].val;
}
int res=0;
int mid=(l+r)>>1;
if(x<=mid) res+=query(tr[u].ls,l,mid,x,y);
if(mid<y) res+=query(tr[u].rs,mid+1,r,x,y);
return res;
}
void update(int x,int y,int val){
if(x==0) return ;
for(int i=x;i<=k;i+=lowbit(i)){
modify(rt[i],1,k,y,val);
}
}
int qry(int x,int y){
int res=0;
for(int i=x;i;i-=lowbit(i)){
res+=query(rt[i],1,k,1,y);
}
return res;
}
int Ans[K<<1];
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>p[i].a>>p[i].b>>p[i].c;
}
sort(p+1,p+1+n,cmp);
int cnt=1;
for(int i=1;i<=n;i++){
if(p[i].a==p[i+1].a && p[i].b==p[i+1].b && p[i].c==p[i+1].c){
cnt++;
continue;
}else{
update(p[i].b,p[i].c,cnt);
int ans=qry(p[i].b,p[i].c);
Ans[ans]+=cnt;
cnt=1;
}
}
for(int i=1;i<=n;i++){
cout << Ans[i] << '\n';
}
return 0;
}
例题F:最大异或和
可持久化 01 Trie 模板题
正常的最大异或和问题肯定就按位贪心就行了。
但是这个题是区间的,所以我们考虑像主席树一样可持久化一下。
树上扔一个 \(cnt\) 表示这个节点存不存在,剩下的事主席树模板。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=6e5+10;
int n,m,a[N];
int rt[N],tr[N<<5];
int son[N<<5][2];
int tot=1;
void insert(int now,int pre,int t,int x){
if(t<0) return ;
int i=(x>>t)&1;
son[now][!i]=son[pre][!i];
son[now][i]=tot++;
tr[son[now][i]]=tr[son[pre][i]]+1;
insert(son[now][i],son[pre][i],t-1,x);
}
int query(int now,int pre,int t,int x){
if(t<0) return 0;
int i=(x>>t)&1;
if(tr[son[pre][!i]]>tr[son[now][!i]]){
return (1<<t)+query(son[now][!i],son[pre][!i],t-1,x);
}else{
return query(son[now][i],son[pre][i],t-1,x);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
rt[0]=tot++;
insert(rt[0],0,25,0);
for(int i=1;i<=n;i++){
int b;cin>>b;
a[i]=a[i-1]^b;
rt[i]=tot++;
insert(rt[i],rt[i-1],25,a[i]);
}
for(int i=1;i<=m;i++){
char op;
cin>>op;
if(op=='A'){
int x;cin>>x;
n++;
a[n]=a[n-1]^x;
rt[n]=tot++;
insert(rt[n],rt[n-1],25,a[n]);
}else{
int l,r,x;
cin>>l>>r>>x;
l--,r--;
if(l==0) cout << query(0,rt[r],25,x^a[n]) << '\n';
else cout << query(rt[l-1],rt[r],25,x^a[n]) << '\n';
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号