基本算法(部分)
算法库:
1.简单排序算法+排序函数
2.枚举算法
3.模拟算法
4.高精度算法
5.贪心算法
6.递归分治算法
-------------------------------------------------------------------------------------------------------------------------------------
简单排序算法:
1.选择排序:
基本思想:
把待排序的 n 个元素看作一个有序部分和一个无序部分。开始时有序部分为空,无序部分包含 n 个元素。排序时每次从无序部分中选出最小的元素,把它与无序部分的第一个元素交换位置,那么该元素必大于(或等于)有序部分中的所有元素,从而使有序部分元素个数增 1,无序部分元素个数减 1。经过 n-1 次选择和交换后,有序部分有 n-1 个元素,无序部分只有 1 个元素,且该元素大于(或等于)有序部分中的所有元素,整个排序过程结束。
排序过程:
基本代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int a[200]; 4 int main() 5 { 6 int n; 7 cin>>n; 8 for(int i=1;i<=n;i++)cin>>a[i]; 9 for(int i=1;i<=n-1;i++) 10 { 11 int p=a[i]; 12 int m=i; 13 for(int j=i+1;j<=n;j++) 14 { 15 if(a[j]<p) 16 { 17 p=a[j]; 18 m=j; 19 } 20 } 21 swap(a[i],a[m]); 22 } 23 for(int i=1;i<=n;i++)cout<<a[i]<<" "; 24 return 0; 25 }
2.冒泡排序:
基本思想:
具体过程如下:
排序过程
具体代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int a[100],n; 4 int main() 5 { 6 cin>>n; 7 for(int i=1;i<=n;i++)cin>>a[i]; 8 for(int i=1;i<=n-1;i++) 9 for(int j=n-1;j>=i;j--) 10 if(a[j]>a[j+1]) 11 swap(a[j],a[j+1]); 12 for(int i=1;i<=n;i++)cout<<a[i]<<" "; 13 return 0; 14 }
3.插入排序:
基本思想:
排序过程:
基本代码:
1 #include<iostream> 2 using namespace std; 3 int a[100],n; 4 int main() 5 { 6 cin>>n; 7 for(int i=1;i<=n;i++)cin>>a[i]; 8 for(int i=1;i<=n-1;i++) 9 { 10 p=a[i]; 11 for(int j=i-1;j>=1;j--) 12 { 13 if(a[j]>p)a[j+1]=a[j]; 14 else 15 { 16 a[j+1]=p;break; 17 } 18 } 19 } 20 for(int i=1;i<=n;i++)cout<<a[i]<<" "; 21 return 0; 22 }
4.桶排序
基本思想:
桶排序作用:
通常使用场景:
与前几个排序算法区别:
嘿嘿...因为桶排不是"真正的"排序算法,所以没有过程^_^..
不过...没有基本代码...怎么办怎么办....
那我们就来做道题吧...
P1059 [NOIP2006 普及组] 明明的随机数
题目描述
明明想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了 NN 个 11 到 10001000 之间的随机整数 (N\leq100)(N≤100),对于其中重复的数字,只保留一个,把其余相同的数去掉,不同的数对应着不同的学生的学号。然后再把这些数从小到大排序,按照排好的顺序去找同学做调查。请你协助明明完成“去重”与“排序”的工作。
输入格式
输入有两行,第 11 行为 11 个正整数,表示所生成的随机数的个数 NN。
第 22 行有 NN 个用空格隔开的正整数,为所产生的随机数。
输出格式
输出也是两行,第 11 行为 11 个正整数 MM,表示不相同的随机数的个数。
第 22 行为 MM 个用空格隔开的正整数,为从小到大排好序的不相同的随机数。
输入输出样例
10 20 40 32 67 40 20 89 300 400 15
8 15 20 32 40 67 89 300 400
参考代码如下:
1 #include <bits/stdc++.h> 2 using namespace std; 3 int sum,bus[1002]; 4 int main(){ 5 int n,x; 6 scanf("%d",&n); 7 for(int i=1;i<=n;i++){ 8 cin>>x; 9 if(bus[x]) 10 continue; 11 bus[x]++; 12 sum++; 13 } 14 printf("%d\n",sum); 15 for(int i=1;i<=1000;i++) 16 if(bus[i]) 17 printf("%d %",i); 18 return 0; 19 }
排序函数:
基本代码:
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 int a[100],n; 5 int main() 6 { 7 cin>>n; 8 for(int i=1;i<=n;i++)cin>>a[i]; 9 sort(a+1,a+1+n); 10 for(int i=1;i<=n;i++)cout<<a[i]<<" "; 11 return 0; 12 }
基本代码:
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 int a[100],n; 5 bool cmp(int x,int y) 6 { 7 return x>y; 8 } 9 int main() 10 { 11 cin>>n; 12 for(int i=1;i<=n;i++)cin>>a[i]; 13 sort(a+1,a+1+n,cmp); 14 for(int i=1;i<=n;i++)cout<<a[i]<<" "; 15 return 0; 16 }
-----------------------谢谢观看--------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
枚举算法:
枚举算法概念:
枚举算法解题基本思路:
常见一般格式:
枚举算法的常用优化方法:
枚举算法的优缺点:
优点:
缺点:
最后:
例题:百钱买百鸡:
参考代码(有错误,仔细看)

解决方法:

根据题意,设鸡翁、鸡母、鸡雏其值为x,y,z。可以列出下面的不定式方程


完整代码如下:
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 for(int i=0;i<=20;i++) 6 { 7 for(int j=0;j<=33;j++) 8 { 9 int k=100-i-j;//这里注意一下要声明类型 10 if(i*15+j*9+k==300) 11 { 12 cout<<i<<" "<<j<<" "<<k<<endl; 13 } 14 } 15 } 16 }
-------------------谢谢观看--------------------
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
模拟算法:
模拟算法的概念:
【例】1893:玩具谜题
【题目描述】
小南有一套可爱的玩具小人,它们各有不同的职业。有一天,这些玩具小人把小南的眼镜藏了起来。小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
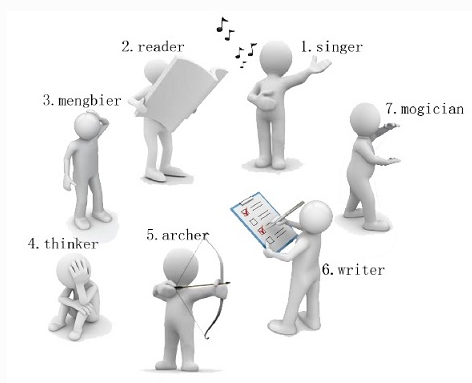
这时singer告诉小南一个谜题:“眼镜藏在我左数第3个玩具小人的右数第1个玩具小人的左数第2个玩具小人那里。”
小南发现,这个谜题中玩具小人的朝向非常关键,因为朝内和朝外的玩具小人的左右方向是相反的:面朝圈内的玩具小人,它的左边是顺时针方向,右边是逆时针方向;而面向圈外的玩具小人,它的左边是逆时针方向,右边是顺时针方向。
小南一边艰难地辨认着玩具小人,一边数着:
“singer朝内,左数第3个是archer。
“archer朝外,右数第1个是thinker。
“thinker朝外,左数第2个是writer。
“所以眼镜藏在writer这里!”
虽然成功找回了眼镜,但小南并没有放心。如果下次有更多的玩具小人藏他的眼镜,或是谜题的长度更长,他可能就无法找到眼镜了。所以小南希望你写程序帮他解决类似的谜题。这样的谜题具体可以描述为:
有n个玩具小入围成一圈,己知它们的职业和朝向。现在第1个玩具小人告诉小南一个包含m条指令的谜题,其中第i条指令形如“左数/右数第Si个玩具小人”。你需要输出依次数完这些指令后,到达的玩具小人的职业。
【输入】
输入的第一行包含两个正整数n,m,表示玩具小人的个数和指令的条数。
接下来n行,每行包含一个整数和一个字符串,以逆时针为顺序给出每个玩具小人的朝向和职业。其中0表示朝向圈内,1表示朝向圈外。保证不会出现其他的数。字符串长度不超过10且仅由小写字母构成,字符串不为空,并且字符串两两不同。整数和字符串之间用一个空格隔开。
接下来m行,其中第i行包含两个整数ai,Si,表示第i条指令。若ai=0,表示向左数Si个人;若ai=1,表示向右数Si个人。保证ai不会出现其他的数,1<si<n。
【输出】
输出一个字符串,表示从第一个读入的小人开始,依次数完m条指令后到达的小人的职业。
【输入样例】
7 3 0 singer 0 reader 0 mengbier 1 thinker 1 archer 0 writer 1 mogician 0 3 1 1 0 2
【输出样例】
writer
【提示】
【样例2输入】
10 10 1 c 0 r 0 p 1 d 1 e 1 m 1 t 1 y 1 u 0 v 1 7 1 1 1 4 0 5 0 3 0 1 1 6 1 2 0 8 0 4
【样例2输出】
y
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
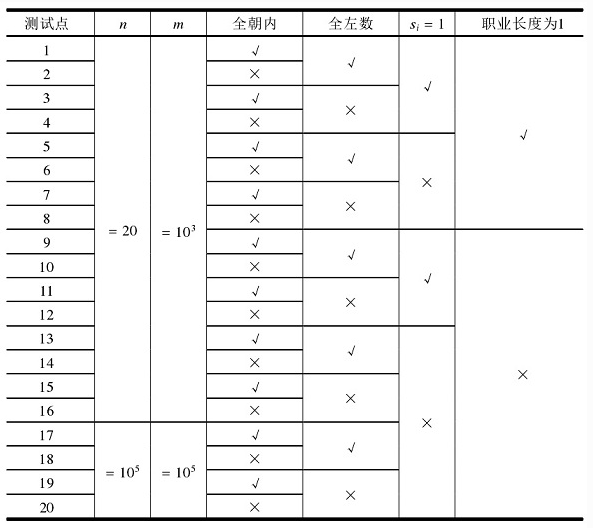
其中一些简写的列意义如下:
·全朝内:若为“√”,表示该测试点保证所有的玩具小人都朝向圈内;
·全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的 1<i<m, ai=0;
·Si=1:若为“√”,表示该测试点保证所有的指令都只数1个,即对任意的 1≤i≤m, Si=1;
·职业长度为1:若为“√”,表示该测试点保证所有玩具小人的职业一定是一个 长度为1的字符串。
参考代码如下:
1 /* 2 数组 q 记录 n 个人的朝向 3 0 表示面向圈内,向左对应位置减小,向右对应位置增大; 4 1 表示面向圈外,向左对应位置增大,向右对应位置减小。 5 朝向(0/1) == 左右(0/1),位置减小,否则位置增大 6 n 个人围成一圈,可以考虑用[0,n)表示位置,通过 % 运算来处理圈的问题 */ 7 #include <cstdio> 8 const int maxn=100010; 9 int n,m,q[ maxn ]; //q[i]:第i个人的朝向 10 int d,k; //d:0-向左;1-向右 11 char ss[ maxn ][15]; //职业 12 int main () 13 { 14 scanf ("%d%d" ,&n ,&m) ; 15 for(int i=0;i<n;i++) scanf ("%d%s" ,&q[i] ,ss[i]) ; 16 int cur =0; // 当前位置 17 for(int i=0;i<m;i++) 18 { 19 scanf ("%d%d" ,&d ,&k) ; 20 if(q[cur ]== d) cur =( cur -k+n) %n; 21 else cur =( cur +k) %n; 22 } 23 printf ("%s\n",ss[cur ]) ; 24 return 0; 25 }
---------------------谢谢观看-------------------
----------------------------------------------------------------------------------------------------------
高精度算法:
高精度数的存储:
高精度数的存储基本用char类型的数组先存储,再转成int类型
如何转int类型:
首先,我们先获取char类型数组的长度;
然后用for循环一位一位的转化,转化可以﹣‘0’也可以﹣48\
普通代码:
1 #include <bits/stdc++.h> 2 #include <cstring> 3 using namespace std; 4 char a[10001]; 5 int a1[10001]; 6 int main() 7 { 8 cin>>a; 9 int lena=strlen(a); 10 for(int i=0;i<lena;i++) 11 { 12 a1[i]=a[i]-48; 13 } 14 return 0; 15 }
高级一点的代码:
1 /* 2 读入:以字符串形式读入 3 存储:小端存储(个位放最前面)。位数(长度)放在 a[0],把个位数存在 a[1],十位数存在 a[2],依次类推; 4 */ 5 #include <bits/stdc++.h> 6 #include <cstring> 7 using namespace std; 8 char ss[10001]; 9 int a[10001]; 10 void read (int *a) 11 { 12 scanf ("%s", ss) ; 13 a[0] = strlen (ss) ; 14 for(int i = 1; i <= a [0]; i++) 15 { 16 a[i] = ss[a[0] - i] - '0'; 17 } 18 } 19 int main() 20 { 21 read(a); 22 }
高精度加法:
考虑非负整数的高精度加法,参考小学学习过的竖式加法演算形式,模拟实现高精度加法。
普通代码:
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 char a[1000],b[1000]; 5 int a1[1000],b1[1000],c[1000]; 6 int lena,lenb,lenc,lenmax,x; 7 int main() 8 { 9 cin>>a>>b; 10 lena=strlen(a); 11 lenb=strlen(b); 12 for(int i=0;i<lena;i++) 13 { 14 a1[i]=a[lena-1-i]-48;//输入转倒序 15 } 16 for(int i=0;i<lenb;i++) 17 { 18 b1[i]=b[lenb-1-i]-48;//输入转倒序 19 } 20 lenmax=max(lena,lenb); 21 while(lenc<lenmax)//也可以用for() 22 { 23 c[lenc]=a1[lenc]+b1[lenc]+x; 24 x=c[lenc]/10; 25 c[lenc]%=10; 26 lenc++; 27 } 28 if(x) c[lenc]=x; 29 else lenc--; 30 for(int i=0;i<=lenc;i++) 31 { 32 33 cout<<c[lenc-i];//倒序输出 34 } 35 return 0; 36 }
高级一点的代码:
1 /* 2 读入:以字符串形式读入 3 存储:小端存储(个位放最前面)。位数(长度)放在 a[0],把个位数存在 a[1],十位数存在 a[2],依次推; 4 */ 5 #include <bits/stdc++.h> 6 #include <cstring> 7 using namespace std; 8 char ss[10001]; 9 int a[10001],b[10001]; 10 void read (int *a) 11 { 12 scanf ("%s", ss) ; 13 a[0] = strlen (ss) ; 14 for(int i = 1; i <= a [0]; i++) 15 { 16 a[i] = ss[a[0] - i] - '0'; 17 } 18 } 19 void add (int *a, int *b) 20 { // a += b 2 a[0] = max(a[0] , b [0]) ; 21 int cr = 0; //cr 表示进位 22 for(int i=1; i <=a [0]; i++) 23 { //逐位计算 24 a[i] += b[i] + cr; //a[i]+b[i]+进位cr 25 cr = a[i] / 10; //计算新的进位 7 a[i] %= 10; 26 } 27 if(cr) 28 { //最高位有进位 29 a [0]++; 30 a[a [0]] = cr; 31 } 32 } 33 int main() 34 { 35 read(a);read(b);add(a,b); 36 for(int i = a [0]; i; i--) printf ("%d", a[i]) ; 37 printf ("\n") ; 38 return 0; 39 }
高级一点的代码2.0版
1 /* 2 读入:以字符串形式读入 3 存储:小端存储(个位放最前面)。位数(长度)放在 a[0],把个位数存在 a[1],十位数存在 a[2],依次推; 4 */ 5 #include <bits/stdc++.h> 6 #include <cstring> 7 using namespace std; 8 char ss[10001]; 9 int a[10001],b[10001]; 10 void read (int *a) 11 { 12 scanf ("%s", ss) ; 13 a[0] = strlen (ss) ; 14 for(int i = 1; i <= a [0]; i++) 15 { 16 a[i] = ss[a[0] - i] - '0'; 17 } 18 } 19 void add (int *a,int *b) // a += b 2 a [0]= max(a[0] ,b [0]) ; 20 { 21 for(int i=1;i <=a [0]; i++) 22 { 23 a[i]+=b[i]; //对应位置求和 24 } 25 for(int i=1;i <=a [0]; i++) 26 { //处理进位 27 a[i+1]+= a[i]/10; 28 a[i]%=10; 29 } 30 //如果最高位有进位,位数增 1 31 if(a[a [0]+1]) a [0]++; 32 //处理可能多余的位数 33 while (a[0] > 1 && !a[a [0]]) a[0] - -; 34 } 35 int main() 36 { 37 read(a);read(b);add(a,b); 38 for(int i = a [0]; i; i--) printf ("%d", a[i]) ; 39 printf ("\n") ; 40 return 0; 41 }
高精度减法:
普通代码:
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 char a[1000],b[1000]; 5 int a1[1000],b1[1000],c[1000]; 6 int lena,lenb,lenc,lenmax,x; 7 int main() 8 { 9 cin>>a>>b; 10 lena=strlen(a); 11 lenb=strlen(b); 12 for(int i=0;i<lena;i++) 13 { 14 a1[i]=a[lena-1-i]-48;//输入转倒序 15 } 16 for(int i=0;i<lenb;i++) 17 { 18 b1[i]=b[lenb-1-i]-48;//输入转倒序 19 } 20 for(int i=0;i<lena;i++) 21 { 22 c[i]=a1[i]-b1[i]-x; 23 if(c[i]<0) 24 { 25 c[i]+=10; 26 x=1; 27 } 28 else 29 { 30 x=0; 31 } 32 } 33 for(int i=lena-1;i>0;i--) 34 { 35 if(c[i]==0) 36 { 37 lena--; 38 } 39 else 40 { 41 break; 42 } 43 } 44 for(int i=lena-1;i>=0;i--) 45 { 46 cout<<c[i]; 47 } 48 return 0;
高级一点的代码:
1 /* 2 读入:以字符串形式读入 3 存储:小端存储(个位放最前面)。位数(长度)放在 a[0],把个位数存在 a[1],十位数存在 a[2],依次推; 4 */ 5 #include <bits/stdc++.h> 6 #include <cstring> 7 using namespace std; 8 char ss[10001]; 9 int a[10001],b[10001]; 10 void read (int *a) 11 { 12 scanf ("%s", ss) ; 13 a[0] = strlen (ss) ; 14 for(int i = 1; i <= a [0]; i++) 15 { 16 a[i] = ss[a[0] - i] - '0'; 17 } 18 } 19 void sub (int *a,int *b) // a -= b (约定a ≥ b) 20 { 21 for(int i=1;i <=a [0]; i++) 22 { 23 if(a[i] <b[i]) 24 { // 借位 25 a[i]+=10; 26 a[i+1]--; 27 28 } 29 a[i]-=b[i]; 30 } 31 //重新确定位数 32 for (;a [0] >1&& a[a [0]]==0; a[0]--) ; 33 } 34 int main() 35 { 36 read(a);read(b);sub(a,b); 37 for(int i = a [0]; i; i--) printf ("%d", a[i]) ; 38 printf ("\n") ; 39 return 0; 40 }
高精度乘法:
乘法运算,考虑两种情况:
1.高精度数乘小整数:
mul1(int *a, b) 相当于高精度数的每个数字a[i]扩了b倍,再处理进位及位数。
普通代码:
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 char a[1000]; 5 int a1[1000],b1[1000],c[1000]; 6 int lena,lenb,lenc,lenmax,x,s; 7 int main() 8 { 9 int b; 10 cin>>a>>b; 11 if(b==0) 12 { 13 cout<<0; 14 return 0; 15 } 16 lena=strlen(a); 17 for(int i=0;i<lena;i++) 18 { 19 a1[i+1]=a[i]-48; 20 } 21 for(int i=lena;i>=0;i--) 22 { 23 s=a1[i]*b+x; 24 x=s/10; 25 b1[i]=s%10; 26 } 27 int i=0; 28 while(b1[i]==0&&i<lena) 29 { 30 i++; 31 } 32 for(;i<=lena;i++) 33 { 34 cout<<b1[i]; 35 } 36 return 0; 37 }
高级一点的代码:
1 /* 2 读入:以字符串形式读入 3 存储:小端存储(个位放最前面)。位数(长度)放在 a[0],把个位数存在 a[1],十位数存在 a[2],依次推; 4 */ 5 #include <bits/stdc++.h> 6 #include <cstring> 7 using namespace std; 8 char ss[10001]; 9 int a[10001],b[10001]; 10 void read (int *a) 11 { 12 scanf ("%s", ss) ; 13 a[0] = strlen (ss) ; 14 for(int i = 1; i <= a [0]; i++) 15 { 16 a[i] = ss[a[0] - i] - '0'; 17 } 18 } 19 void mul1 (int *a, int b) // a *= b; 20 { 21 for(int i = 1; i <= a [0]; i++) 22 { 23 a[i] *= b; 24 } 25 for(int i = 1; i <= a [0]; i++) 26 { 27 a[i + 1] += a[i] / 10; 28 a[i] %= 10; 29 } 30 while (a[a[0] + 1]) //如果更高位非零 31 { 32 a [0]++; //位数增 1 33 a[a[0] + 1] = a[a[0]] / 10; //再向高位进位 34 a[a[0]] %= 10; 35 } 36 } 37 int main() 38 { 39 int b1; 40 cin>>b1; 41 read(a);mul1(a,b1); 42 for(int i = a [0]; i; i--) printf ("%d", a[i]) ; 43 printf ("\n") ; 44 return 0; 45 }
2.高精度数乘高精度数:
普通代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 #define LENGTH 1001 6 int main(){ 7 char a1[LENGTH],b1[LENGTH]; 8 int a[LENGTH],b[LENGTH],c[LENGTH]; 9 int lena,lenb,lenc,i,j,x; 10 memset(a,0,sizeof(a)); 11 memset(b,0,sizeof(b)); 12 memset(c,0,sizeof(c)); 13 cin>>a1>>b1; 14 lena = strlen(a1); 15 lenb = strlen(b1); 16 for (i = 0;i < lena;i++) 17 { 18 a[lena - i] = a1[i] - 48; 19 } 20 for (i = 0;i < lenb; i++) 21 { 22 b[lenb - i] = b1[i] - 48; 23 } 24 25 for (i = 1; i <= lena; i++) 26 { 27 x = 0; 28 for (j = 1; j <= lenb; j++) 29 { 30 31 c[i + j - 1] = a[i] * b[j] + x + c[i + j - 1]; 32 x = c[i + j - 1] / 10; 33 c[i + j - 1] %= 10; 34 } 35 c[lenb + i] = x; 36 } 37 lenc = lena + lenb; 38 while (c[lenc] == 0 && lenc > 1) 39 { 40 lenc--; 41 } 42 for (i = lenc; i >= 1; i--) 43 { 44 cout<<c[i]; 45 } 46 return 0; 47 }
高级一点的代码:
1 # include <cstdio> 2 # include <cstring> 3 const int maxl = 210; 4 char ss[ maxl ]; 5 int a[ maxl ] , b[ maxl ] , c[ maxl * 2]; 6 void read (int *a) 7 { 8 scanf ("%s", ss) ; a[0] = strlen (ss) ; 9 for(int i = 1; i <= a [0]; i++) a[i] = ss[a[0] - i] - '0'; 10 } 11 void mul () { 12 c[0] = a[0] + b[0] - 1; 13 for(int i = 1; i <= a [0]; i++) 14 { 15 for(int j = 1; j <= b [0]; j++) 16 { 17 c[i + j - 1] += a[i] * b[j]; 18 } 19 } 20 for(int i = 1; i <= c [0]; i++) 21 { 22 c[i + 1] += c[i] / 10; c[i] %= 10; 23 } 24 if(c[c[0] + 1]) c [0]++; 25 while (c[0] > 1 && !c[c [0]]) c[0]--; // 处理乘以 0 的情况 26 } 27 int main () { 28 read (a) ; read (b) ; mul () ; 29 for(int i = c [0]; i; i--) printf ("%d", c[i]) ; 30 printf ("\n") ; return 0; 31 }
高精度除法:
我们只讨论高精度数除以小整数,观察除法竖式演算式,不难发现:
逐位求商:每次都是普通整数的 /、%运算
"落位":新的被除数=上一次的余数×10+下一个数字
参考代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int a[100005]; 4 int c[100005]; 5 int main() 6 { 7 string s; 8 int p; 9 cin>>s>>p; 10 long long la=s.size(),x=0; 11 for(int i=0;i<la;i++) 12 { 13 x=x*10+(int)s[i]-'0'; 14 c[i]=x/p; 15 x%=p; 16 } 17 int k=0; 18 while(c[k]==0&&k<la-1) 19 { 20 k++; 21 } 22 for(int i=k;i<la;i++){ 23 cout<<c[i]; 24 } 25 return 0; 26 }
小结:
高精度数的基本运算均与相应的竖式演算式类似,其实现过程是对竖式演算的模拟。
对于高精度数,需维护位数以及用数组来保存的各位数字,进行计算后,应及时处理位数的变化情况。
---------------谢谢观看-----------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
贪心算法:
引例 1

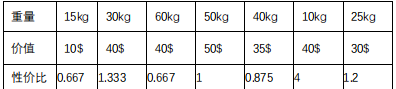
引例 2
什么是贪心算法:
贪心策略:
贪心基本过程:
贪心算法基本证明思路:
例:过河问题
--------------谢谢观看---------------
递归分治算法:
一、递归和分治:
1.用递归解决问题

我们知道递归就是函数的自我调用。可如果递归仅仅
是函数不停地的自我调用,那么它就会陷入一种无意义的死循环中,是无法解决问题的。
所以今天我们再深化理解递归解决问题真正原理。
2、 再看汉诺塔问题
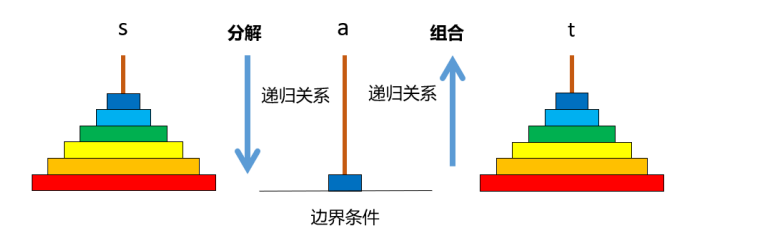
我们想解决 6 层汉诺塔问题时,由于这个问题比较复杂,于是我们把这个复杂的问
题分解成三部:即先把上面的五个盘子移动到辅助柱上,这样我们就能很容易地把最底
下的盘子移动到目标柱。然后再把在辅助柱子上的五个盘子移动到目标柱。由于上层五
个盘子正好可以看作是一个五层汉诺塔,所以实际上我们把一个六层汉诺塔问题分解为
完成两个 5层汉诺塔问题,再加一步(移动最底层盘子)。
虽然问题没有得到最终的解决,但是我们踏出了重要的一步:即把一个复杂问题转
化为相对简单的问题。(规模更小的汉诺塔问题的组合)。
3、 递归是形式,分治是策略
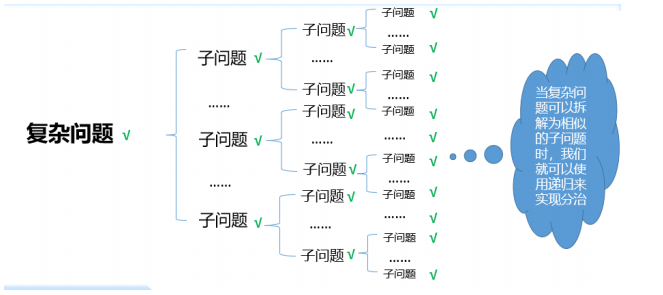
把复杂问题拆解为相对简单的问题,直到无法拆解为止。然后通过简单的问
题的解决,累积解决复合问题,直到最终问题得以解决。这就是分治策略。
另外,如果每个子问题结构都各不相同,就无法用统一的方法去解决它们。所以
只有把子问题想办法拆解成和母问题相似的结构,才方便使用递归的形式来实
现。从这个角度来看,递归是程序实现的形式,而分治是解决问题的策略。
二、排序中的分治策略:
1、简单插入排序
给定n个自然数,对其的排序(升序)问题可以分解为:
a、先将前 n-1个数排序
b、将第 n 个数插入已经有序前 n-1个数组成的数列中

参考代码:


2.二路归并排序
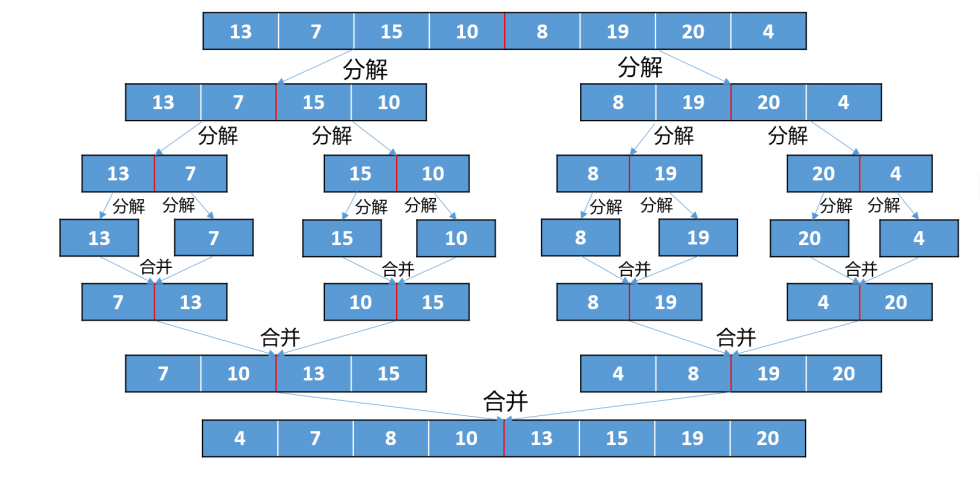
归并排序的分治策略:
1、将原数列按照位置中分前后两个子列,分别将其排序(分解)
2、待两个子列已经有序,再将它们合并成一个有序数列(组合)
归并排序中的合并操作:
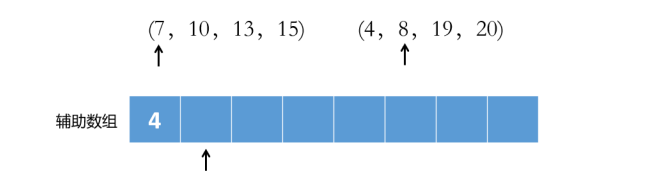
a、 比较前后两个子列的队首元素,将较小的插入辅助数组(重复)
b、 直到有一个子列已经全部插入辅助数组
c、 将尚有待插入元素的子列中剩余元素按序插入辅助数组
d、 辅助数组按下标回填原数组
参考代码:


参考代码:

3.快速排序
快速排序的分治策略:
a、先取数组中的某一个元素作为一个基准元素(首元素/中点位置/随机位置)
b、调整基准元素到数组中合适的位置,同时对其他元素进行调整,使得在基准元素的右边
的所有元素都不小于它,而基准元素左边的元素都不大于它。
c、然后再对基准元素的前后两个区间分别进行快速排序,直到每个区间为空或者只有一个元素时,
整个快速排序结束。
如何划分不大于和不小于基准元素:

参考代码:




参考代码:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号