[NOI2003]逃学的小孩【观察+树的直径】

Online Judge：Bzoj1509，Luogu P4408

Label：观察，树的直径

题目描述

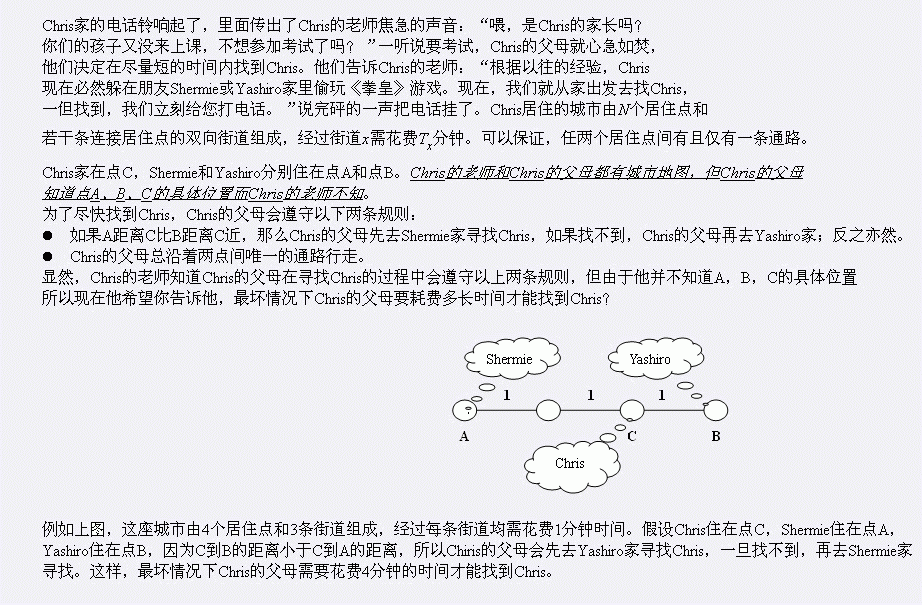
输入

第一行是两个整数N（\(3≤N≤200000\)）和M，分别表示居住点总数和街道总数。以下M行，每行给出一条街道的信息。第i+1行包含整数Ui、Vi、Ti（\(1≤Ui, Vi ≤ N，1≤Ti≤1000000000\)），表示街道i连接居住点Ui和Vi，并且经过街道i需花费Ti分钟。街道信息不会重复给出。

输出

仅包含整数T，即最坏情况下Chris的父母需要花费T分钟才能找到Chris。

样例

Input

4 3
1 2 1
2 3 1
3 4 1

Output

4

题解

【大致题意】

在树上选三个点，设家在A，现在要去B，然后再从B到C。请你求出最大的总路程\(AB+BC\)，且满足\(AB<AC\)。

假设现在已经确定了路径\(BC\)，该如何去找最优的\(A\)？预处理两个数组\(g[i][0/1]\)分别表示点i到端点\(B/C\)的距离，则有\(ans=dis(BC)+max(min(g[i][0],g[i][1]))\)\(i∈[1,n]\)。

回想一个性质，树上离某点i最远的点一定是树直径上两个端点中的一个。根据上面的式子，很明显令\(BC\)为树的直径时答案一定最优。接下来再按上面的方法去找个\(A\)就解决了。

时间复杂度为\(O(N)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+10;
struct node{int to,w;};
vector<node>e[N];

int id1,id2,n,m;
ll ma=0,g[N][2];
void dfs(int x,ll dis,int fa){
	if(dis>ma)ma=dis,id1=x;
	for(int i=0;i<e[x].size();i++){
		int y=e[x][i].to;if(y==fa)continue;
		dfs(y,dis+e[x][i].w,x);
	}
}
void go(int x,ll dis,int fa,int o){
	g[x][o]=dis;
	for(int i=0;i<e[x].size();i++){
		int y=e[x][i].to;if(y==fa)continue;
		go(y,dis+e[x][i].w,x,o);
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,u,v,d;i<=m;i++){
		scanf("%d%d%d",&u,&v,&d);
		e[u].push_back((node){v,d});
		e[v].push_back((node){u,d});
	}
	dfs(1,0,0);
	id2=id1,ma=0;	
	dfs(id1,0,0);
	
	go(id1,0,0,0);go(id2,0,0,1);
	ll now=0;
	for(int i=1;i<=n;i++){
		if(i==id1||i==id2)continue;
		now=max(now,min(g[i][0],g[i][1]));
	}
	printf("%lld\n",now+ma);
}