牛客算法周周练2 小H和游戏 (树/思维)

不得不说，看了别人的代码发现解决的好巧，所以就把它记录下来了。

原题链接：D-小H和游戏

题意：

给一棵 \(N\) 个结点的树，所有结点初始值为 \(0\)，现有 \(Q\) 次操作，每次操作给出结点 \(x\) ,对 \(x\) 以及距离小于等于 \(2\) 的所有点结值加 \(1\),对于每次操作，输出操作后 \(x\) 的值为多少

数据范围：\(N(1\leq N\leq750000)\) \(Q(1≤Q≤750000)\)

思路：

刚拿到题或许会往通过dfs序或者层数之类作为距离的联系，从而更新

但是对于一棵树来说，如下图所示

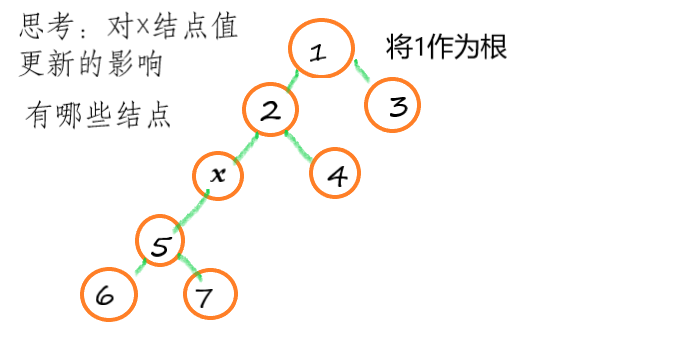
首先是 \(x\) 本身

其次是其父节点，和祖先结点，也就是 \(1和2\)

然后是所有兄弟结点 \(4\)

其所有子结点 \(5\) 和 子孙结点 \(6,7\)

再思考如何表示，能够把其兄弟的贡献，子与子孙结点的贡献求出来。父和祖先结点也就是其本身更新的次数。

我们使用一个数组\(f[]\)记录其父结点，用\(num[当前结点][距离]\) 来表示当前结点对距离\(x\)的影响

然后我们发现，兄弟的贡献即时 \(num[当前结点的父亲][1]\), 子与子孙结点的贡献为 \(num[当前结点][1],num[当前结点][2]\)，所以从而获得总贡献\(num[q][1] + num[q][2] + num[f[q]][0] + num[f[q]][1] + num[f[f[q]]][0](0,表示距离为0也就是其本身操作的次数)\)

所以得到以下代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 750005;
vector<int>E[maxn];
int f[maxn];
int num[maxn][3];//下标、距离
map<int,int>vis;
int N,Q;

void dfs(int q,int fa){
    f[q] = fa;
    for(int i=0;i<(int)E[q].size();i++){
        int v = E[q][i];
        if(v!=fa){
            dfs(v,q);
        }
    }
}
int main(){
    scanf("%d%d",&N,&Q);
    for(int i=1;i<N;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        E[u].push_back(v);
        E[v].push_back(u);
    }
    dfs(1,0);
    for(int i=1;i<=Q;i++){
        int q; 
        scanf("%d",&q);
        num[q][0]++;//自己本身
        if(f[q]) num[f[q]][1]++;//父节点
        if(f[f[q]]) num[f[f[q]]][2]++;//祖结点
        int ans;
        if(q == 1) ans = num[q][1] + num[q][2] + num[q][0];
        else ans = num[q][1] + num[q][2] + num[f[q]][0] + num[f[q]][1] + num[f[f[q]]][0];
        printf("%d\n",ans);
    }
}