st表

st表

1简洁

st表可以 \(nlogn\) 预处理，O1查询，相对于线段树的 \(\log n\) 查询相对有优势，但是 st 表只能支持静态解决 RMQ，这是一个非常大的劣势。

2.讲解

ST 表是利用的是倍增的思想

拿最大值来说

我们用 \(𝑀𝑎𝑥[𝑖][𝑗]\) 表示，从 \(𝑖\) 位置开始的 \(2^j\) 中的最大值，例如 \(𝑀𝑎𝑥[𝑖][1]\) 表示的是 \(𝑖\) 位置和 \(𝑖+1\) 位置中两个数的最大值

那么转移的时候我们可以把当前区间拆成两个区间并分别取最大值（注意这里的编号是从 \(1\) 开始的）

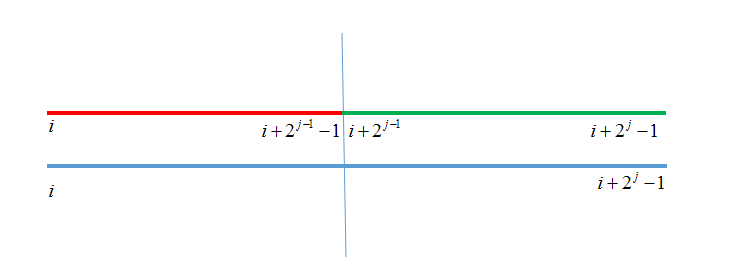
查询的时候也比较简单

我们计算出 \(𝑙𝑜𝑔_2\) (区间长度)

然后对于左端点和右端点分别进行查询，这样可以保证一定可以覆盖查询的区间

显然我们可以得到 \(𝑥=𝑟−2^𝑘+1\)

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<queue>
#define N 100010
#define ll long long
using namespace std;

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

int n,m,a[N],f[N][21];

inline void build_st(){
	for(int i=1;i<=n;i++) f[i][0]=a[i];
	for(int j=1;j<=20;j++){
		for(int i=1;i+(1ll<<j)-1<=n;i++){
			f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
		}
	}
}

inline int ask_max(int l,int r){
	int len=log2(r-l+1);
	return max(f[l][len],f[r-(1ll<<len)+1][len]);
}

int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	build_st();
	for(int i=1;i<=m;i++){
		int l,r;l=read();r=read();
		printf("%d\n",ask_max(l,r));
	}
	return 0; 
}

引用注明

st表