多路查找树
特点:每个结点的孩子可以有多于两个孩子,且每个结点处可存放多个元素,所以元素之间存在某种特定的排序关系
B-树:
- 一颗m阶的B-树,或为空树,或为满足下列特性的m叉树
- 树中每个结点至多有m颗子树;
- 除根节点之外的所有非终端结点至少有 ┍ m/2 ┑ 颗子树
- 若根节点不是叶子结点,则至少有两颗子树
- 所有的叶子结点都必须出现在同一层次上,
- 所有的非终端结点最多有m-1个关键字
1 #define m 3 //B-树的阶,暂定为3 2 3 typedef struct BTNode{ 4 int keynum; //结点中关键字的个数,结点的大小 5 struct BTNode *parent; //指向双亲结点 6 KeyType k[m+1]; //关键字数组,0号单元不使用 7 struct BTNode *ptr[m+1]; //子树指针数组 8 Record *recptr[m+1]; //记录指针数组,0号元素未用 9 }BTNode,*BTree; //B-树结点和B-树类型 10 11 typedef struct{ 12 BTNode *pt; //指向找到的结点 13 int i; //1..m,在结点中的关键字序号 14 int tag; //1:查找成功;0:查找失败 15 }Result; //B-树的查询结果类型
- 查找:
将给定值key与根节点的各个关键字K₁,K₂,...,Kj(1≤j≤m-1)进行比较,由于该关键字序列有序,所以查找时可采用顺序查找,也可采用二分查找。查找时:
- 若key=Ki(1≤i≤j),则查找成功
- 若key<k₁,则顺着P0所指向的子树继续向下查找
- 若Ki<key<i+1(1≤i≤j-1),则顺着Pi所指向的子树继续向下查找
- 若key>Kj,则顺着指针Pj所指向的子树继续向下查找
如果在自上而下的查找过程中,找到了值为key的关键字,则查找成功;但如果直到叶子结点也未找到,则查找失败。
Result SearchTree(BTree T,Keytype key){ //在m阶B-树T上查找关键字key,返回结果(pt,i,tag) //若查找成功,则特征值tag=1,指针pt所指向结点中第i个关键字等于key //若特征值tag=0,等于key的关键字应该插入在指针pt所指向结点中第i和第u+1个关键字之间 BTree p=T,q=NULL; bool fount=FALSE; int i=0; while(p&&!fount){ i=Search(p,key); //在p->K[1,,keynum]中查找i,使得p->K[i]<=key<p->k[i+1] if(i>0&&p->K[i]==key) fount=TRUE;//找到待查找关键字 else {q=p;p=p->ptr[i];} } if(fount) return (p,i,1);//查找成功 else return (q,i,0);//查找不成功,返回key的插入位置信息 }
可见,在B-树中进行查找包含两个基本操作:1、在B-树中找到结点;(硬盘中进行)2、在结点中找到关键字(内存中进行)
该查关键字所在结点在B-树上的层数,是决定B-树查找效率的首要因素
- 插入:
由于B-树中除根之外的所有非终端结点中的关键字个数必须大于等于┍ m/2 ┑-1,因此,每次插入一个关键字不是在树中添加一个叶子结点,而是首先在最低成某个非终端结点中添加一个关键字,若该结点个关键字个数不超过m-1,则插入完成,否则表明结点已满,要产生新结点的“分裂”。
分裂方法:以中间关键字为界把结点一分为二,称为两个结点,并把中间关键字向上插入到双亲结点上,若双亲结点已满则采用同样的方法继续分解。最坏的情况下,一直分解到根结点,这时B-树的高度加1。
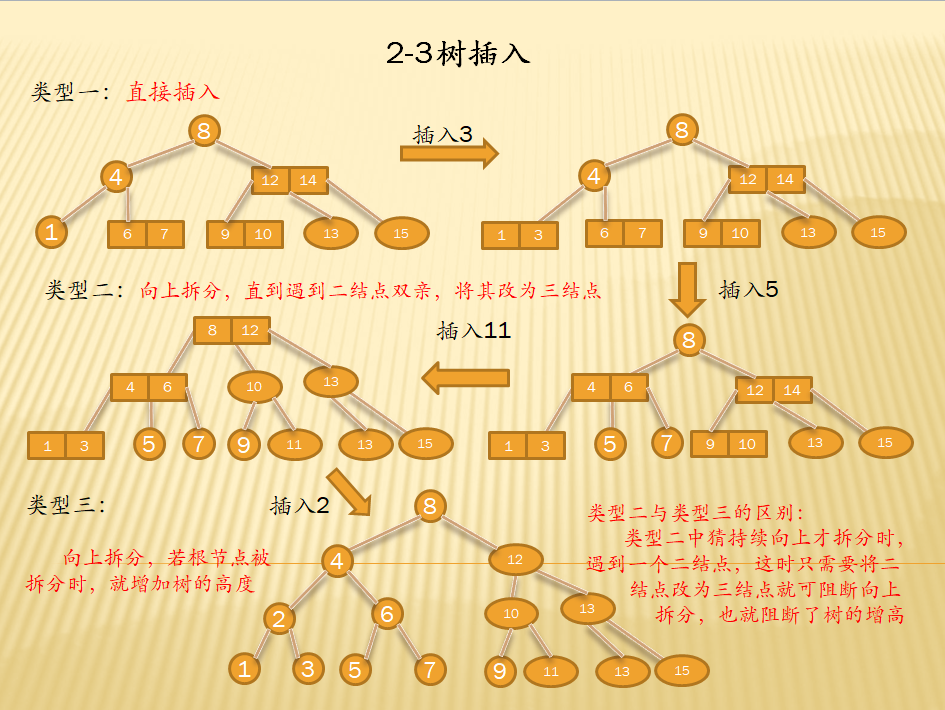
- 在B-树中查找给定关键字的记录,若查找成功,则插入的操作失败;否则将新纪录作为空指针ap插入到查找到失败的叶子结点的上一层结点(由q指向)中
- 若插入新纪录和空指针后,q指向的结点关键字个数未超过m-1,则插入操作成功,否者转向步骤 3
- 以该结点的第┍ m/2 ┑个关键字为拆分处,将该结点分为3部分:┍ m/2 ┑左边部分,第┍ m/2 ┑个关键字,┍ m/2 ┑右边部分。然后:┍ m/2 ┑左边部分仍然保留在原结点中;┍ m/2 ┑右边部分存放在一个新建立的结点(由ap指向)中;关键字值为┍ m/2 ┑的记录和指针ap插入到q的双亲结点中。因q的双亲结点添加一个新的记录,所以必须对q的双亲结点的重复步骤2和步骤3。以此类推,直到由q指向的结点是根结点,转向步骤4
- 由于根结点无双亲,则分裂产生的两个结点的指针q和ap,以及关键字为第┍ m/2 ┑个记录构成一个新的根结点(二结点)。此时,B-树的高度增加1。
1 Status InsertBTree(BTree &T,Keytype key,BTree q,int i){ 2 //在m阶B-树T上结点*q的K[i]与K[i+1]之间插入关键字key 3 //若引起节点过大,则沿双亲链表进行必要的结点分裂调整,使T仍然是m阶B-树 4 Keytype x=key;//x表示新插入的关键字 5 BTree ap=NULL; 6 bool finished=FALSH; 7 while(q&&!finished){ 8 Insert(q,i,x,ap);//将x和ap分别插入到q->key[i+1]和q->ptr[i+1]上 9 if(!q->keynum<m) finished=TRUE;//插入完成 10 else{ 11 s=(m+1)/2; 12 split(q,s,ap);//结点为分割两半,右边一般存储在ap中 13 x=q->k[s]; 14 q=q->parent; 15 if(q) i=Search(q,x);//在双亲结点*q中查找x的插入位置 16 } 17 } 18 if(!finished)//T是空树(参数q的初始值为NULL)或者根结点已经分裂称了*q和*ap 19 NewRoot(T,q,x,ap);//生成含信息(T,x,ap)的新的根结点*T,原T和ap为子树指针 20 return OK; 21 }
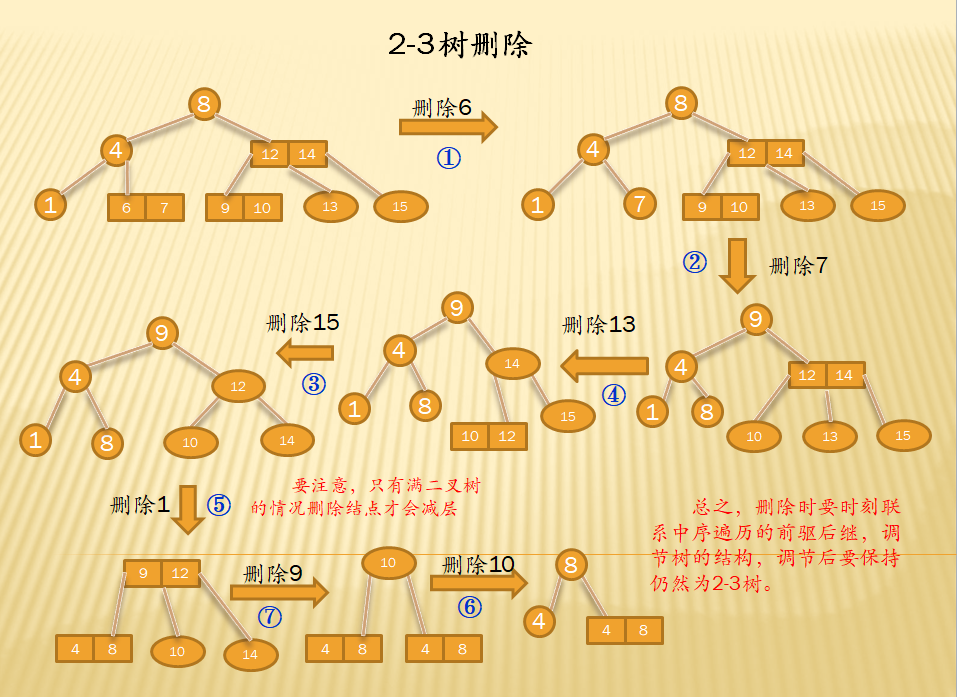
- 删除:
m阶B-树的删除操作是在B-树的某个结点中删除指定的关键字记附近的一个指针,删除后应给进行调整使该树仍然满足B-树的定义,也就是保证每个结点的关键字数目范围为 [┍ m/2 ┑-1,m-1]。删除记录之后,结点的关键字个数如果小于┍ m/2 ┑-1,则要进行“合并”结点的操作。除了删除记录,还要删除该记录附近的指针。若该结点为最下层的非终端结点,由于指针均为空,删除记录后不会影响其他结点,可直接删除;若不是最下层的非终端结点,临近指针则指向一棵树,不可删除。所以可以转化为删除最下非层终端节点的问题
转化方法:将要删除记录用其右(左)边邻近指针的指向的子树中关键字最小(最大)的记录(该记录必在最下层的终端结点中)替换。采用这种方法进行处理,无论是删除记录是否在最下层非终端结点,都可以归结为在最下层的非终端结点中删除记录的情况。而删除最下层非终端结点中的关键字情形有3中可能
- 被删关键字所在结点中的关键字数目不小于┍ m/2 ┑:直接删除即可
- 被删关键字所在结点中的关键字数目等于┍ m/2 ┑-1:将兄弟结点中最小(或最大)的关键字上移至双亲结点中,而将双亲结点中小于(或大于)且紧靠该上移关键字的关键字下移至被删除关键字所在结点中
- 被删除关键字所在结点和其相邻的兄弟结点中关键字数目均等于┍ m/2 ┑-1:它所在的结点中剩余的关键字和指针,加上双亲结点中个关键字Ki一起,合并到Pi所指兄弟结点中。如果因此双亲结点中关键字数目小于┍ m/2 ┑-1,则依次类推做相应处理
B+树
- 概念:B+树是B树的一个升级版,相对于B树来说,B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别
- 一颗 m 阶 B- 树和 B+ 树的区别:
- 有n颗子树的结点中含有n个关键字
- 所有的叶子结点中包含了全部关键字的信息,以及指向含这些关键字记录的指针,且叶子结点本身依关键字大小自小而大的顺序链接
- 所有的非终端结点可以看成是索引部分,结点中仅含有其子树(根结点)中的最大(或最小)关键字
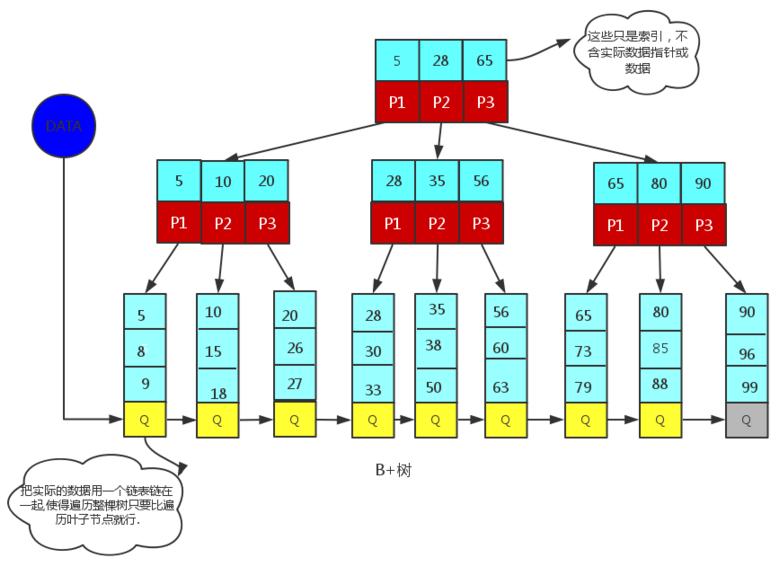
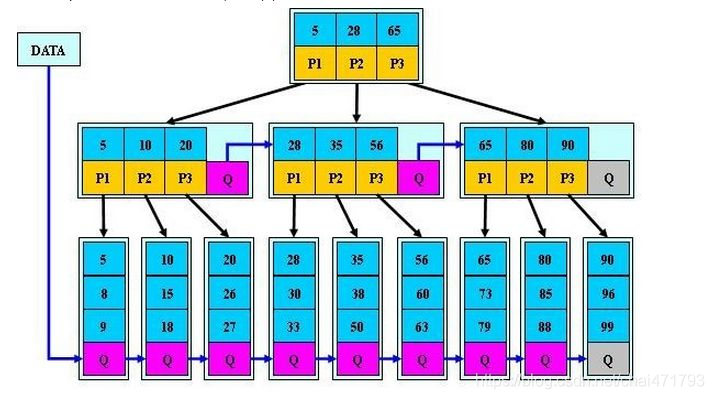
通常在B+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。因此,可以对B+树进行两种查找运算:一是从最小关键字其顺序查找,另一种是从根节点开始,进行随机查找(在B+树上进行随机查找、插入和删除的过程上基本与B-树类似)
- 查找:若非终端结点上的关键字等于给定值,并不终止,而是继续向下直到叶子结点。因此,在B+树中,不管查找成功与否,每次查找都是走了一条从根节点到叶子结点的路径。B+树查找的分析类似于B-树(B+树不仅能有效的查找某个关键字,而且更适合查找某范围的内的所有关键字)
- 插入:仅在叶子结点上进行插入,当结点中的关键字个数大于m时要分裂两个结点,它们所含关键字的个数分别为┕m/2┙和┍ m/2 ┑;并且,它们的双亲结点中间应同时包含这两个结点中的最大关键字。
- 删除:B+树的删除也仅在叶子结点进行,当叶子结点中最大关键字被删除时,其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字的个数少于┍ m/2 ┑时,其和兄弟结点的合并过程也与B-树类似。
B*树
- 规则
B*树是B+树的变种,相对于B+树他们的不同之处如下:
- 首先是关键字个数限制问题,B+树初始化的关键字初始化个数是cei(m/2),b树的初始化个数为(cei(2/3m))
- B+树节点满时就会分裂,而B*树节点满时会检查兄弟节点是否满(因为每个节点都有指向兄弟的指针),如果兄弟节点未满则向兄弟节点转移关键字,如果兄弟节点已满,则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来;
- 特点
在B+树的基础上因其初始化的容量变大,使得节点空间使用率更高,而又存有兄弟节点的指针,可以向兄弟节点转移关键字的特性使得B*树额分解次数变得更少;
B树总结
- 相同思想和策略:从平衡二叉树、B树、B+树、B*树总体来看它们的贯彻的思想是相同的,都是采用二分法和数据平衡策略来提升查找数据的速度;
- 不同的方式的磁盘空间利用:不同点是他们一个一个在演变的过程中通过IO从磁盘读取数据的原理进行一步步的演变,每一次演变都是为了让节点的空间更合理的运用起来,从而使树的层级减少达到快速查找数据的目的;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号