图的存储结构

　　线性表：一对一的关系，所以用数组和链表均可存放

　　树结构：一对多的关系，将数组和链表的特性结合起来存放

　　　　（数组结点：存放数据，双亲下标，指向孩子下标链表的指针；孩子下标的链表：自己的下标，指向兄的指针）

　　图：多对多的情况，另外图上任何一个顶点都可以看做第一个顶点。任一顶点的邻接点之间也不存在依次关系

邻接矩阵(无向图)：

　　图可以分成两个结构分别存储顶点信息，边/弧的信息

  • 顶点：不区分大小，主次关系，所以可用一个一维数组存放
  • 边/弧：由顶点与顶点之间的联系，所以可用一个二维数组存储

注：无向图构成存储边的二维数组是对称矩阵，所以邻接矩阵中浪费了一般的空间（0代表不相关，1代表相关）

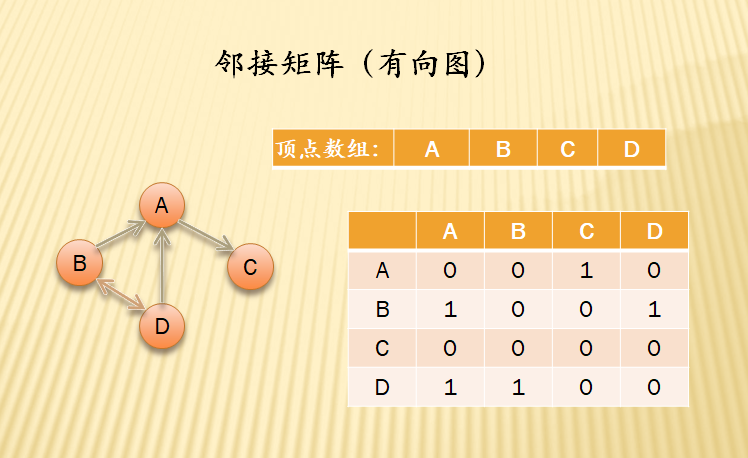
注：有向图中，出度为矩阵对应行中1的数目，入度为对应列中1的数目

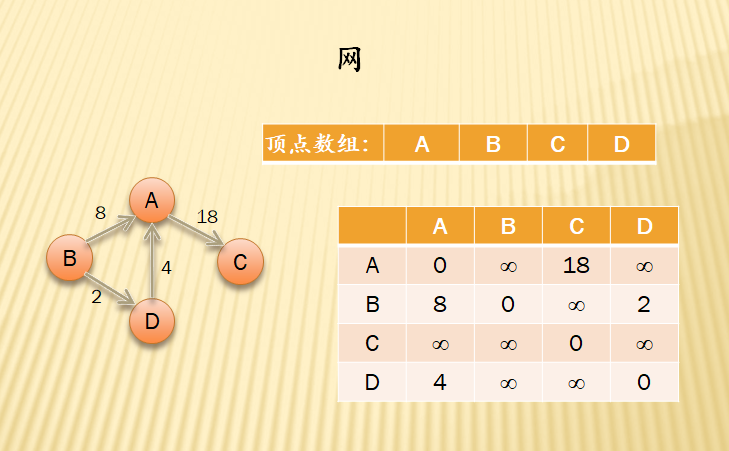
注：网的弧关系矩阵，直接存放这个弧的权（0表示指向自己，‘∞’表示无弧，意为无穷大）

邻接表

　　对于图中边或弧相对较少时，用邻接矩阵则会造成巨大的空间浪费

  • 顶点：用一个一维数组存储
  • 图中每个顶底 Vi 的所有邻接点构成一个线性表，由于邻接点个数不确定，所以选用单链表来存储。

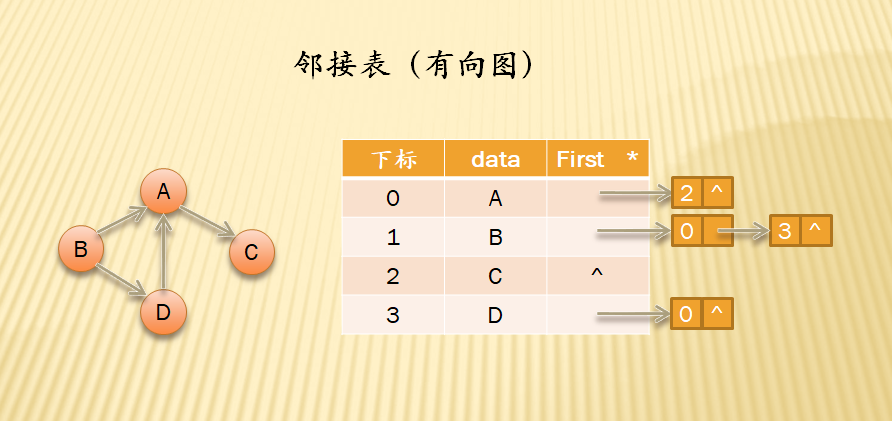
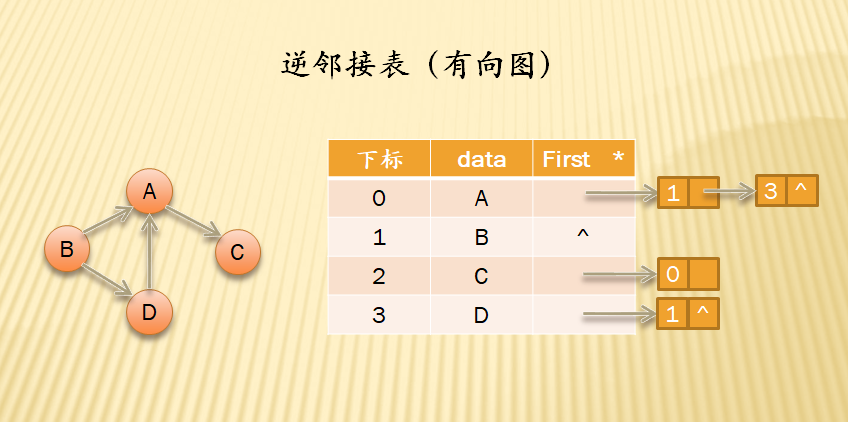
由图中可以看出，邻接表中，便于确定出度或以顶底为弧尾的弧；相应的有时候为了确定入度或以顶点为弧头的弧，便建立了逆邻接点；

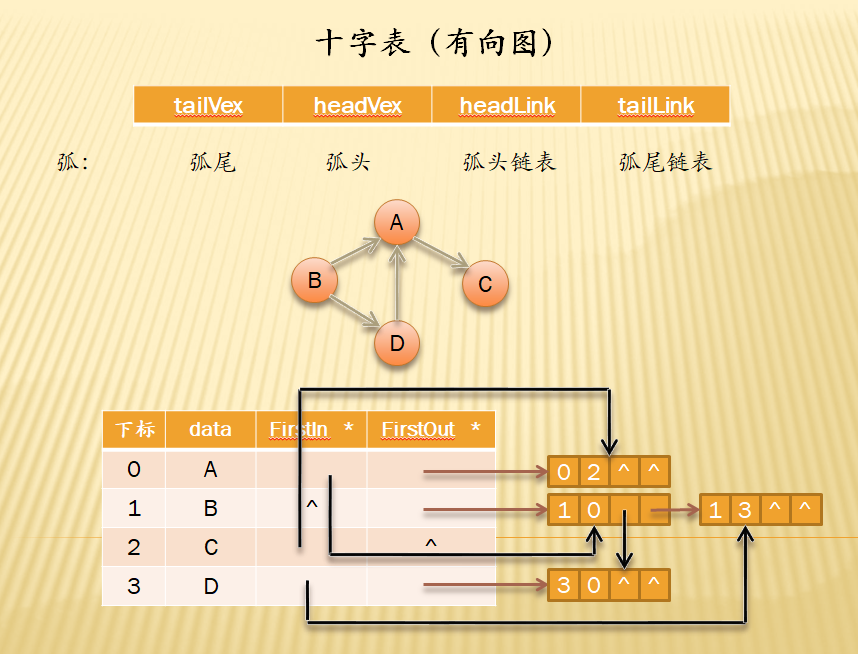
十字链表

　　由于上面的邻接表和逆邻接表都只能单一的入度或者出度，对于无向图是可以全部逻辑关系的，但遇上有向图却是有些缺陷，所以十字链表就很好的把邻接表和逆邻接表结合在了一起

  • 邻接表中边表（链表）的结构：表示一个点（结点结构：弧头或者弧尾下标；指针，指向下一个出度或者入度的结点）
  • 十字链表中边表结点的结构：表示以个弧（结点结构：弧尾下标；弧头下标；弧头链表（链表中的弧头都一样）；弧尾链表（链表中的弧尾都一样））【弧尾链表相当于邻接表；弧头代相当于逆邻接表】

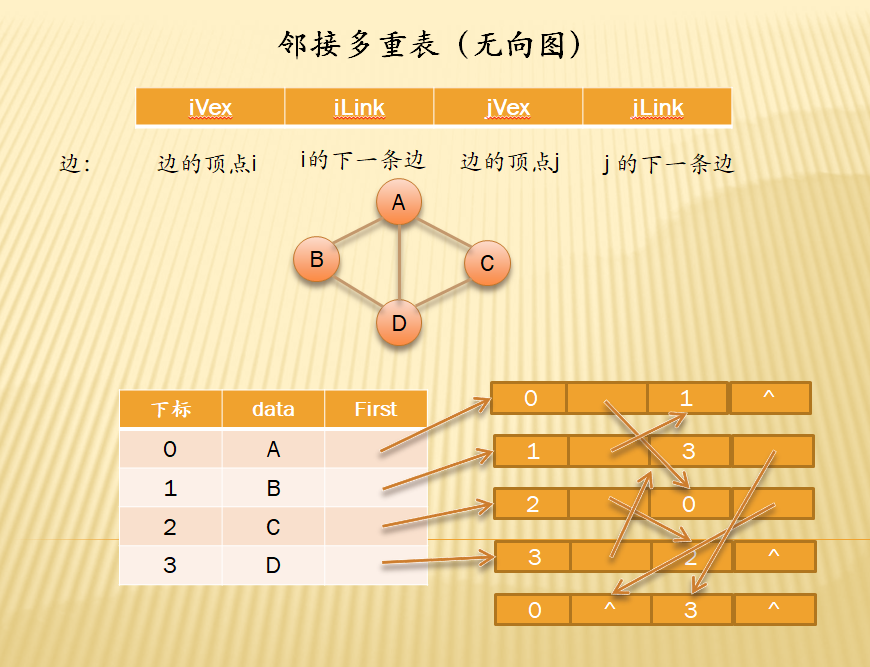
邻接多重表

　　无向图中用邻接表访问结点虽然较为方便，但访问 边的时候却是效率不高，所以根据十字链表的方式为无向图构建出了邻接多重表

  • 邻接多重表的中边表结点结构：表示一条边（iVex 和 jVex 是边依附的两个顶点在顶点表中的下标结构。iLink指向依附顶点 iVex 的下一条边，jLink 指向依附顶点 jVex 的下一条边）

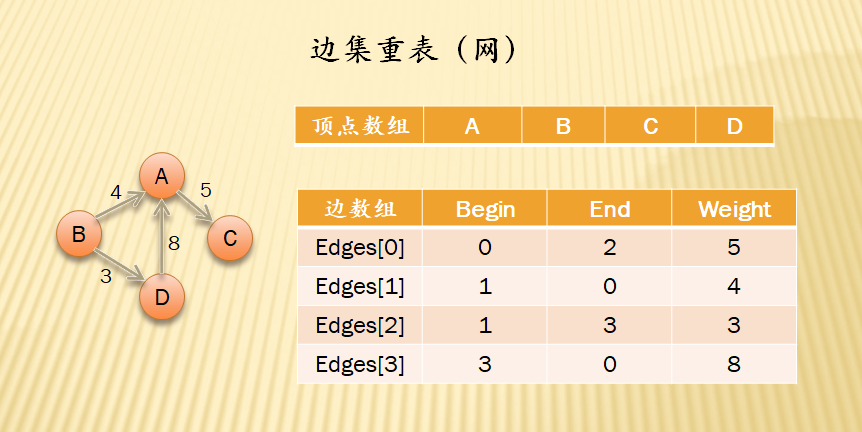
边集数组

　　由两个一维数组构成，一个是存储顶点信息，另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标。终点下标和权组成

  • 相当于邻接矩阵改造版本