树的定义

　　树是 n(n>=0) 个结点的有限集（是一种一对多的数据结构）。当 n=0 时就是空树；

  • 根节点有且只有一个
  • 除根节点外的每个集合本身又是一棵树，称数根的子树（子树个数没有没有限制，并且他们互不相交）
  • 结点的度：该节点拥有子树的数量
  • 树的度：取树中各结点的度的最大值
  • 叶子结点（终端结点）：度为0的结点
  • 分支结点：度不为0的结点；分支中出去根结点外的其余节点又称为内部结点
  • 结点的层次：从根节点开始，根为第一层；根的孩子为第二层；...
  • 树的高度/深度：树中结点的最大层数

树的存储结构

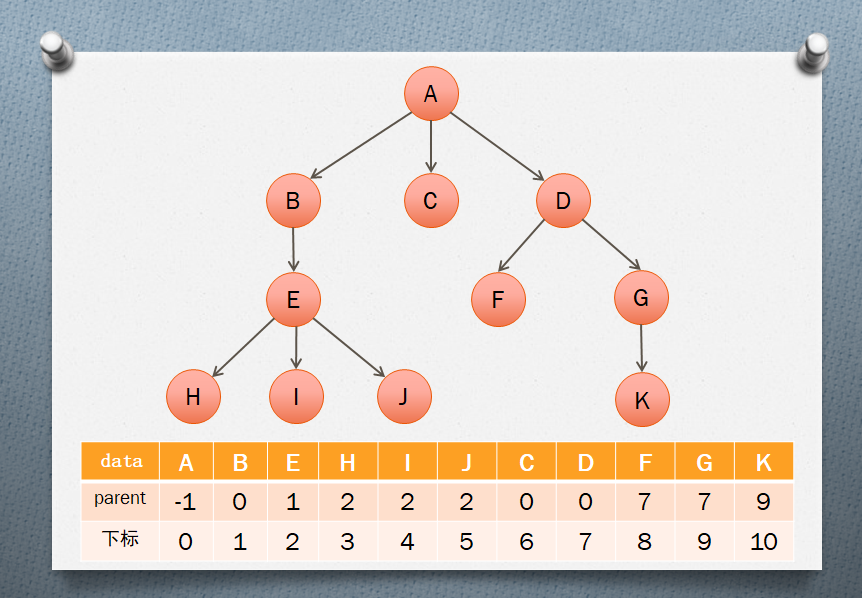
　　1、双亲表示法：假设以一组连续空间存储树的结点，同时在每个节点中附设一个指示器双亲的结点在数组中的位置元素

　　　　时间复杂度；查找双亲结点，O(1)；查找子结点，O(n)；

 1 #define MAX_TREE_SIZE 20
 2 typedef int ElemType;
 3 
 4 typedef struct PTNpde{
 5     ElemType data;//结点数据
 6     int parent;//双亲下标
 7 }PTNode;
 8 
 9 typedef struct{
10     PTNode nodes[MAX_TREE_SIZE];
11     int r;//根结点下标
12     int n;//节点数目
13 }PTree;

例如：

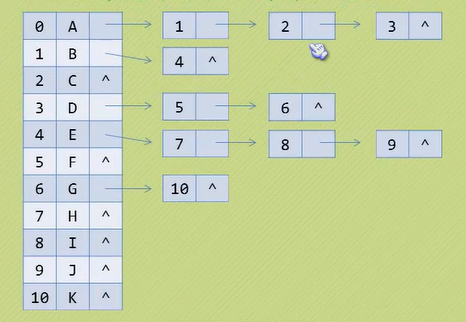
　　2、孩子表示法：由于树的每个结点可能有多颗树，可考虑用多重链表实现。

　　　　相比较双亲表示法，把数组中表示双亲的下标元素改为指向单链表的指针；单链表中存放子结点的下标。

　　3、双亲孩子表示法：将双亲表示法和孩子表示法结合在一起

 1 #define MAX_TREE_SIZE 20
 2 typedef int ElemType;
 3 
 4 typedef struct CTNpde{//孩子结点
 5     int child;//孩子结点的下标
 6     CTNode *next;//指向下一个孩子节点（本节点的兄弟）
 7 }* childPtr;
 8 
 9 typedef struct{//表头结构
10     ElemType data;
11     int parent;//双亲下标
12     childPrt firstchild;//指向子节点链表的指针
13 }CTBox;
14 
15 typedef struct{//树结构
16     CTBox nodes[MAX_TREE_SIZE];
17     int r;//根结点下标
18     int n;//节点数目
19 }Tree;