25五一数据结构专题
0 前言
今天主要内容为数据结构,上午的一些线性数据结构和其他一些较为简单的我就不写了,这里就写写较难的。
1 P3528 [POI 2011] PAT-Sticks:堆拓展
1.1 题面简述
有 \(k\) 种不同颜色的木棍,每种颜色的木棍长度不一。问这些木棍中是否存在三根木棍,是否能够组成一个边长颜色各不相同的三角形。
1.2 思路简述
对每种颜色开一个堆。
再开一个堆,第一次将 \(k\) 个堆的堆顶加入这个堆中。
取出堆顶三根,判断是否可以构成三角形。
可以则输出。
否则将较短的两根加入堆中,再将最长边所在堆的堆顶加入堆中。
1.3 代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
#define ll long long
struct sticks {
int col, len;
bool operator<(const sticks &T) const {
return len < T.len;
}
};
priority_queue<sticks> q[55];
priority_queue<sticks> a;
int k;
bool sanjiaoxing(sticks x, sticks y, sticks z) {
if (x.len + y.len > z.len && x.len - y.len < z.len && x.col != y.col && x.col != z.col && y.col != z.col)
return true;
return false;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> k;
for (int i = 1; i <= k; i++) {
int n;
cin >> n;
for (int j = 1; j <= n; j++) {
int x;
cin >> x;
q[i].push((sticks){i, x});
}
}
for (int i = 1; i <= k; i++) {
a.push(q[i].top());
}
while (!a.empty()) {
if (a.size() < 3) {
cout << "NIE";
return 0;
}
sticks x = a.top();
a.pop();
sticks y = a.top();
a.pop();
sticks z = a.top();
a.pop();
if (sanjiaoxing(x, y, z)) {
cout << x.col << " " << x.len << " ";
cout << y.col << " " << y.len << " ";
cout << z.col << " " << z.len;
return 0;
} else {
a.push(y);
a.push(z);
if (!q[x.col].empty()) {
a.push(q[x.col].top());
q[x.col].pop();
}
}
}
cout << "NIE";
return 0;
}
2 P10471 最大异或对 The XOR Largest Pair:01-trie树
2.1 题面简述
给定 \(N\) 个整数 \(A_1.A_2, \cdots, A_N\) 中选出两个进行异或计算,求结果最大。
2.2 思路简述
考虑异或性质。
构造01-trie树,贪心做异或。
2.3 代码实现
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e7 + 5;
int n;
int a[maxn];
int ne[maxn][2];
int cnt = 0;
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i--) {
int k = (x >> i) & 1;
if (!ne[p][k]) {
ne[p][k] = ++cnt;
}
p = ne[p][k];
}
}
int query(int x) {
int p = 0, ans = 0;
for (int i = 30; i >= 0; i--) {
int k = (x >> i) & 1;
if (ne[p][k ^ 1]) {
p = ne[p][k ^ 1];
ans |= (1 << i);
} else
p = ne[p][k];
}
return ans;
}
signed main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
insert(a[i]);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, query(a[i]));
}
cout << ans;
return 0;
}
3 P3372 【模板】线段树 1:分治思想
3.1 题面描述
略。
3.2 思路简述
闲话:分治比线段树功能更强大,但相应的时间空间复杂度都比线段树更差。其实所有数据结构都是这样的。
将序列分为几段,约为 \(\sqrt n\) 个。
维护每块的和以及元素数量。
3.3 代码实现
#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
using namespace std;
int n, m;
const int maxn = 1e6 + 5;
int a[maxn];
int cnt[maxn], belong[maxn];
int sum[maxn];
int lz[maxn];
signed main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
int s = sqrt(n);
for (int i = 1; i <= n; i++) {
belong[i] = (i - 1) / s + 1;
}
for (int i = 1; i <= n; i++) {
cnt[belong[i]]++;
sum[belong[i]] += a[i];
}
for (int i = 1; i <= m; i++) {
int op;
cin >> op;
if (op == 1) {
int x, y, v;
cin >> x >> y >> v;
if (belong[x] == belong[y]) {
for (int i = x; i <= y; i++) {
sum[belong[i]] += v, a[i] += v;
}
} else {
for (int i = x; belong[i] == belong[x]; i++) {
a[i] += v;
sum[belong[i]] += v;
}
for (int i = y; belong[i] == belong[y]; i--) {
a[i] += v;
sum[belong[i]] += v;
}
for (int i = belong[x] + 1; i < belong[y]; i++) {
sum[i] += v * cnt[i];
lz[i] += v;
}
}
} else {
int x, y;
cin >> x >> y;
if (belong[x] == belong[y]) {
int ans = 0;
for (int i = x; i <= y; i++) {
ans += a[i] + lz[belong[i]];
}
cout << ans << '\n';
} else {
int ans = 0;
for (int i = x; belong[i] == belong[x]; i++) {
ans += a[i] + lz[belong[i]];
}
for (int i = y; belong[i] == belong[y]; i--) {
ans += a[i] + lz[belong[i]];
}
for (int i = belong[x] + 1; i < belong[y]; i++) {
ans += sum[i];
}
cout << ans << '\n';
}
}
}
return 0;
}
4 P1972 [SDOI2009] HH的项链 && P1494 [国家集训队] 小 Z 的袜子 && P4113 [HEOI2012] 采花:莫队算法
4.1 题面简述
呃呃呃三道题我不写了吧,反正都是区间问题。
4.2 思路简述
呃呃呃并没有完全弄会莫队算法,尽自己可能写吧。
咕咕咕中。
首先我们先考虑这样的一个序列,其中Q1和Q2表示区间的和:
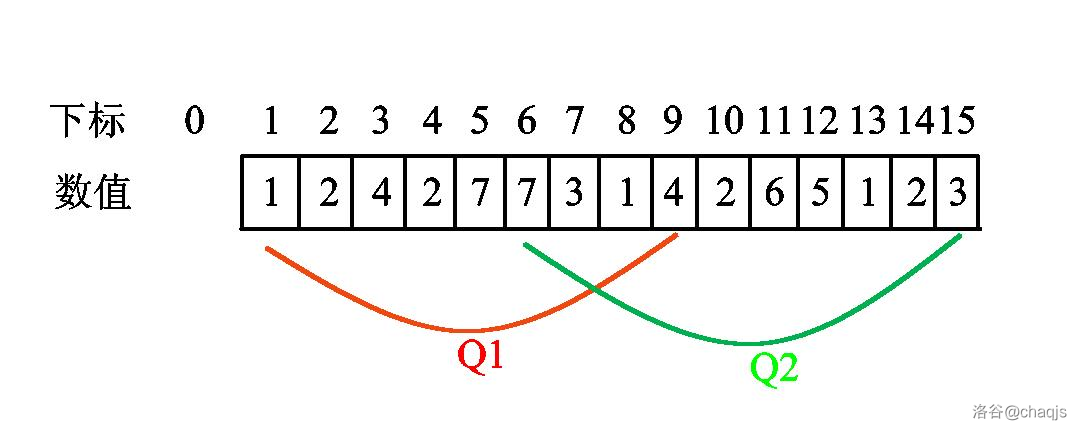
怎样从Q1转移得到Q2呢?
右端点向右移动,动得过程中区间和加上途径的值。
左端点向右移动,动得过程种区间和减去途径的值。
我们将第一个操作称为加入操作。
将第二个操作称为删除操作。
莫队中的加入和删除操作是解决问题的核心。
注意:加入操作是先移动指针,再将指向的值加入;而删除是先将指针所指的值删除,再将指针移动。
但是这种方法还是很容易T。
于是,我们分块处理该序列。再按照右端点从小到大,左端点块编号相同按右端点从小到大排序。
然后按排序后的顺序处理每一个询问,求得答案
再通过一次排序复原原来的顺序。
以上就是普通莫队算法的思想。
对于我来说,还是有一些不太明白。只是差不多懂思路,代码就更别说了。上面的内容多来自网上各种介绍莫队的文章,是我东拼西凑来的。明天钟神还要用一天来讲线段树,所以明天先放下莫队,集训完后在好好研究,明天全力听线段树吧。
下面是参考文章:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号