线段树

时间原因，待更新。

1 引入

已知长度为 \(n\) 的数列 \(a_i\)，你需要进行 \(m\) 次操作，每次操作为下面两种操作之一：

将区间 \([x,y]\) 内每一个数加上 \(k\)。

求出区间 \([x,y]\) 中每一个数的和。

其中，\(1 \le n,m \le 10^5\)，且任意时刻数列的和不超过 \(2 \times 10^{18}\)。

这就需要线段树来解决了。

2 线段树的基本原理

2.1 线段树的概念及建立

（引自 OI-wiki）

线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。

线段树可以在 \((O(\log N)\) 的复杂度内实现单点修改、区间修改、区间查询（求和、最值）等操作。

我们运用分治的思想。例如区间 \([1,8]\)，我们将其划分为下面的结构。

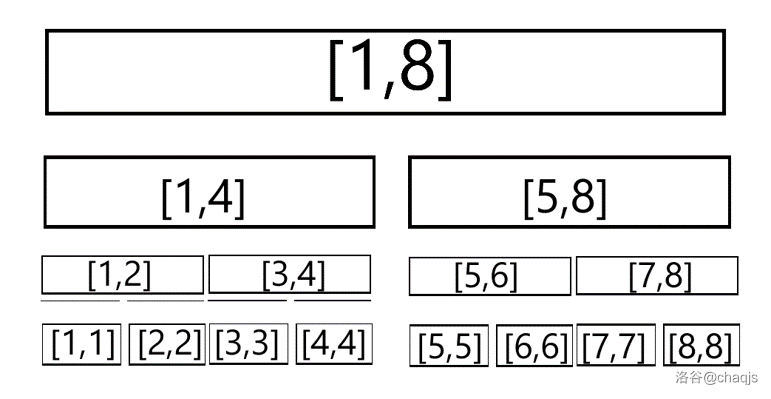
采取这种从中间对半劈开的方法，我们发现任何一个区间都可以表示成这些区间没有交集的并。

例如区间 \([2,6]\) 可以表示为 \([2,2] + [3,4] + [5,6]\)。

于是我们进一步发现，如果在每个结点上维护若干个我们需要的信息，通过这种“信息合并”的方式，我们就可以得到任意区间的信息。

但是需要注意的是，线段树维护的信息必须具有可合并性。

例如，区间 \([1,2]\) 的和加上区间 \([3,3]\) 的和一定是区间 \([1,3]\) 的和，但区间 \([1,3]\) 的众数不一定是区间 \([1,2]\) 的众数和区间 \([3,3]\) 的众数中出现次数较多的。

线段树本质上就是一棵完全二叉树，所以我们回忆二叉树的存储方法。对于结点 \(i\)，它的左子结点编号为 \(2i\)，右子结点编号为 \(2i+1\)。

我们用递归的方法建树，每次将区间分成两个区间分别建树，直到该结点为叶子结点。对于每个叶子结点，它的区间和也就是它本身的值。当然我们还应当有一个信息合并的函数 pushup，这里我们以区间和为例。代码见下。

ll a[N], sum[N << 2];// sum[i]表示结点i存储的区间和 

ll left_son(ll x) { return x << 1; }// x结点的左儿子 
ll right_son(ll x) { return x << 1 | 1; }// x结点的有儿子 

void pushup(ll x) {// 合并信息 
    sum[x] = sum[left_son(x)] + sum[right_son(x)];
}

void build(ll x, ll l, ll r) {// 建树，x表示当前子树的根结点，l和r表示左右端点 
    if (l == r) {// 如果已经递归到叶子结点 
        sum[x] = a[l];// 这个结点的区间和就是a[l]，当然a[r]也可以 
        return ;
    }
    ll mid = (l + r) >> 1;// 取中点 
    build(left_son(x), l, mid);// 建左子树 
    build(right_son(x), mid + 1, r);// 建右子树 
    pushup(x);// 合并左右子树的信息 
}

2.2 单点查询与修改

如何查询一个叶子结点点呢？类似于二分，递归查询该点在左子树中还是右子树中，直到找到这个点。单点修改也一样，不过修改之后别忘了更新以后需要修改的点。代码见下。

ll query1(ll x, ll l, ll r, ll p) {// 在以x为根的子树、l到r的区间中查询编号为p的叶子结点的信息 
    if (l == r) return sum[x];// 找到该结点，返回信息 
    ll mid = (l + r) >> 1;
    if (p <= mid)// 如果在左子树，就递归查询左子树 
        return query1(left_son(x), l, mid, p);
    else// 反之查询右子树 
        return query1(right_son(x), mid + 1, r, p);
}

void update1(ll x, ll l, ll r, ll p, ll w) {// 以x为根的子树、l到r的区间中把p结点修改为w 
    if (l == r) {// 找到该结点，修改 
        sum[x] = w;
        return ;
    }
    ll mid = (l + r) >> 1;
    if (p <= mid)// 与查询一样 
        update1(left_son(x), l, mid, p, w);
    else 
        update1(right_son(x), mid + 1, r, p, w);
    pushup(x);// 别忘了更新 
}

可以发现，每次递归调用都是在线段树上下移一层。由于线段树的树高是 \(\log n\)，所以线段树单点操作的复杂度为 \(O(\log n)\)。

2.3 区间查询

其实单点查询对于线段树来说并没有意义，因为在数组上就可以实现。那怎样实现区间的查询呢？我们分情况讨论。

若当前结点所表示的区间被要查询的区间覆盖，直接返回并传回信息。
若当前结点的左儿子所表示的区间被要查询的区间覆盖，查询它的左儿子。
若当前节点的右儿子所表示的区间被咬查询的区间覆盖，查询它的右儿子。

代码见下。

bool inrange(ll L, ll R, ll l, ll r) {// 判断区间[L, R]是否被[l, r]包含 
	return (l <= L) && (R <= r);
}
bool outofrange(ll L, ll R, ll l, ll r) {// 判断区间[L, R]是否与被[l, r]完全无交集  
	return (L > r) || (R < l);
}

ll query2(ll x, ll l, ll r, ll L, ll R) {// 在以x为根的子树、l到r的区间中查询[L, R] 
	if (inrange(l, r, L, R))
		return sum[x];
	else if (!outofrange(l, r, L, R)) {// 如果有交 
		ll mid = (l + r) >> 1;
		return query2(left_son(x), l, mid, L, R) + query2(right_son(x), mid + 1, r, L, R);
	}
	return 0;// 否则完全无交 
}

2.4 区间修改

显然，如果暴力修改每个叶子结点，时间复杂度无法承受。那该如何处理呢？

这里我们引入懒标记。所谓懒标记，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次修改时，我们对该结点所对应的区间打上懒标记，表示该区间已被修改，然后直接修改该结点的信息并返回。当下一次访问带有标记的结点时，先将懒标记下放到子节点，然后进行递归。

ll lzy[N << 2];
void maketag(ll x, ll len, ll u) {
	lzy[x] += u;
	sum[x] += len * u;
} 

void pushdown(ll x, ll l, ll r) {
	ll mid = (l + r) >> 1;
	maketag(left_son(x), mid - l + 1, lzy[x]);
	maketag(right_son(x), r - mid, lzy[x]);
	lzy[x] = 0;
}

ll query2(ll x, ll l, ll r, ll L, ll R) {// 在以x为根的子树、l到r的区间中查询[L, R] 
	if (inrange(l, r, L, R))
		return sum[x];
	else if (!outofrange(l, r, L, R)) {// 如果有交 
		ll mid = (l + r) >> 1;
		pushdown(x, l, r);
		return query2(left_son(x), l, mid, L, R) + query2(right_son(x), mid + 1, r, L, R);
	}
	return 0;// 否则完全无交 
}

void update(ll x, ll l, ll r, ll L, ll R, ll u) {
	if (inrange(l, r, L, R)) {
		maketag(x, r - l + 1, u);
	}
	else if (!outofrange(l, r, L, R)) {
		ll mid = (l + r) >> 1;
		pushdown(x, l, r);
		update(left_son(x), l, mid, L, R, x);
		update(roght_son(x), mid + 1, r, L, R, u);
		pushup(x);
	}
}

posted @ 2025-02-06 15:30 chaqjs 阅读(18) 评论(0) 收藏举报

刷新页面返回顶部

TianJiajun-chaqjs

线段树

线段树