文远知行杯广东工业大学第十六届程序设计竞赛 A-区间最大值

引理：数论分块

 

关于此处的数学规律，有这样的定理技巧

给定正整数i和n满足i<=n，使得n/i=n/x成立的最大的x为n/(n/i).

也就是说，因为

1.n/i 的值在某一段中是相等的。

2.在 k：i-x 的区间里，n/k 是相等的，那么最大的x也就是区间 [L,R] 的R了，而 L 则是最小的 i。

综上，得到区间

R=n/(n/L);//R的确定
L=R+1//L的更新

通过变形，可以得到%的运算

题目中的定理使用如下

 

 

 

这里的 nk-sum 中的 sum 视作[L,R]区间的所有（k/i）* i 相加，因为（k/i）都一样，所以可以变成

sum=(k/i)*(R-L+1)*(L+R)/2;//区间的等差数列求和 Sn=n*(a1+an)/2;

由此可以求得区间的%和了。

 

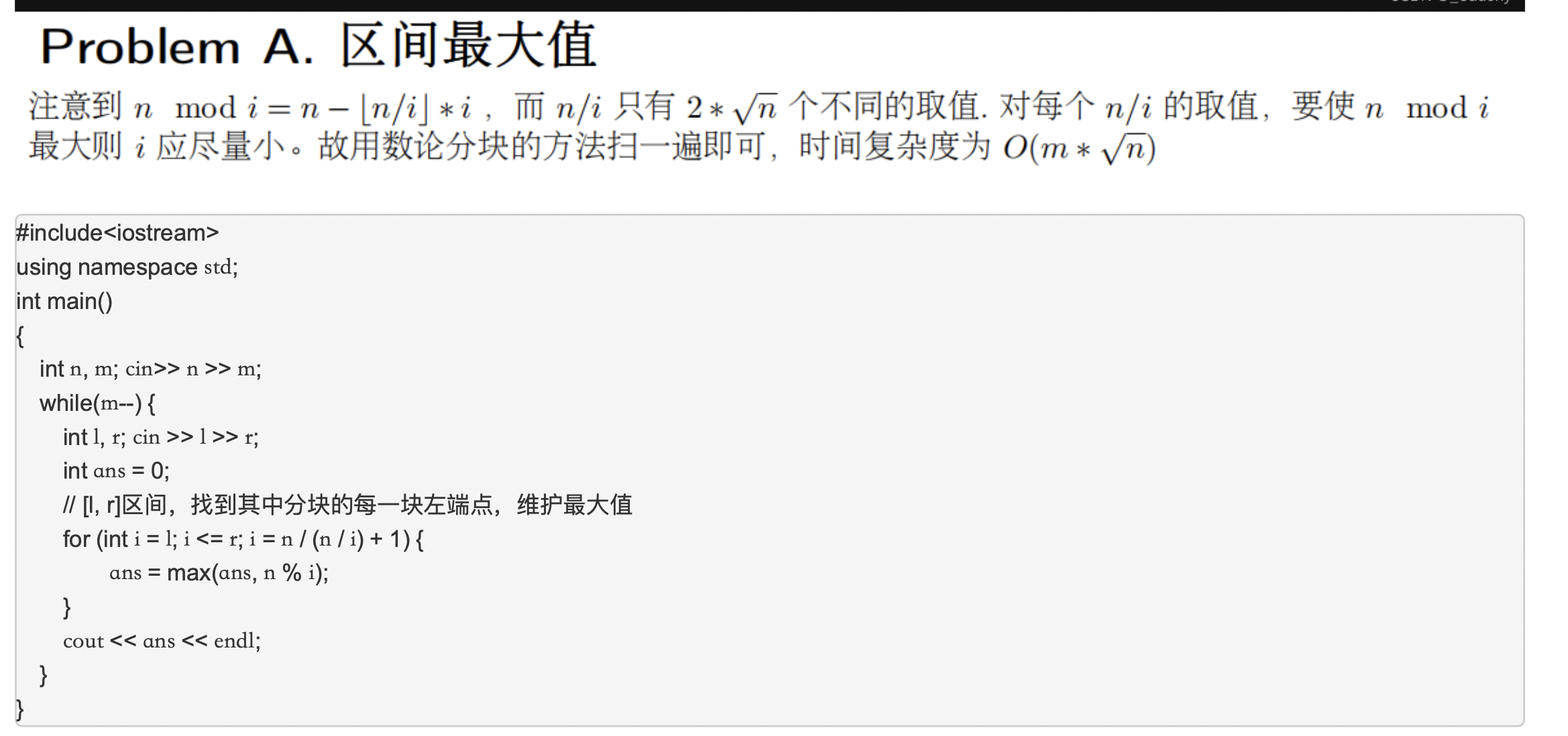
 很妙，求最大，也就是求i最小的时候得到最大，也就是最左端的端点，对于每个分块求的最左端的端点，因为是单点求值，所以不需要使用 [n/i] 的变形来节省时间。

对于每个区间，进行分块操作，每次操作的时间复杂度也很奇妙。

五月了，任重道远。