【笔记】Hash
杂言
话说字符串 \(Hash\) 是真的香,不知为何,我一直很喜欢这种概率性的东西,尤其是这种正确率不稳定的方法,因为当你感觉过不了的时候突然 \(AC\) 的时候那种激动的心情是别的题目不能具有的。
好了,不多说了,开正题。
Hash
\(Hash\) 表又称散列表,一般由 \(Hash\) 函数与了链表结构共同实现。
建立一个大小等于值域的数组进行统计和映射是最简单的 \(Hash\) 思想。——蓝书
好像我也描述不大清,看百度百科吧......
\(Hash\),一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射\(pre-image\))通过散列算法变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。——百度百科。
字符串Hash
终于开正题了。
所谓字符串 \(Hash\) 就是把一个字符串映射成为一个数字,在我理解下就是为了便于查询和查找而产生的一种算法。
对于一个字符串,取一固定值 \(P\) ,可以把字符串看成 \(P\) 进制数,并分配一个大于零的数值,代表每种字符,一般来说,我们分配的数值都远小于 \(P\) 。例如,对于小写字母构成的字符串,可以令 $a = 1,b = 2,\cdots,z = 26 $。取一固定值 \(M\) ,求出该 \(P\) 进制数对 \(M\) 的余数,作为该字符串的 \(Hash\) 值。——蓝书
对于进制数的选择
进制数一定要取一个质数!!!,当你选择一个合数的时候,意味着你和零分差不了多远了。
因为 \(Hash\) 是一种不完全算法,会有冲突的事件产生,例如 \(orzc\) 和 \(orzhjw\) 肯定是不同的,但是他们的 \(Hash\) 值都是 \(233\) ,然后计算机就会认为它们俩一样,出现了哈希冲突。
而合数就会加大这个概率。
推荐进制数 : \(27,131,31,10007,2017\)。
给张表格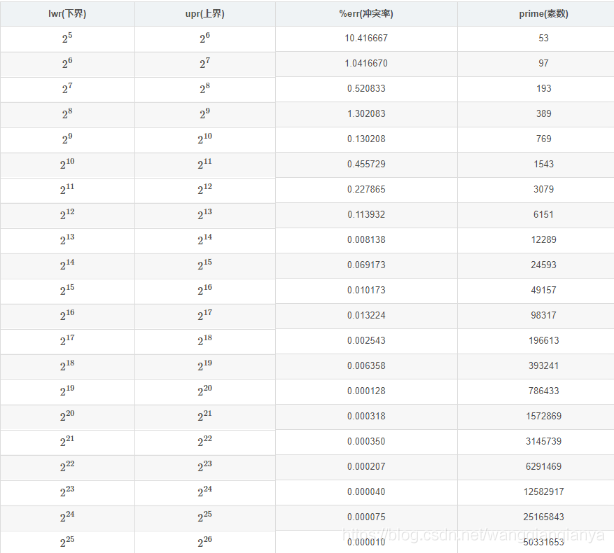
计算哈希值
1.【单哈希】
long long Hash()
{
int len = strlen(s);
long long tot=0;
for(int i = 0;i < len; i ++){
tot =( (tot * p + (long long) s[i]) % mod + mod) % mod;
}
return tot;
}
2.【双哈希】
long long Hash1()
{
int len = strlen(s);
long long tot=0;
for(int i = 0;i < len; i ++){
tot =( (tot * p + (long long) s[i]) % mod1 + mod1) % mod1;
}
return tot;
}
long long Hash2()
{
int len = strlen(s);
long long tot=0;
for(int i = 0;i < len; i ++){
tot =( (tot * p + (long long) s[i]) % mod2 + mod2) % mod2;
}
return tot;
}
也就是把单哈希写两遍,两者都一样的时候才算一样,提高了正确性。
3.【自然溢出哈希】
unsigned long long()
{
int len = strlen(s);
unsigned long long tot=0;
for(int i = 0;i < len; i ++){
tot =(tot * p + (unsigned long long) s[i]);
}
return tot;
}
说实话这种是我做题时写的最多的,一是因为 $unsigned\ long \ long $ 自动取模,省去了取模的时间,二是它好写(by 重度懒癌患者)。
例题
以 $luogu\ 3370 $ 为例。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#define ull unsigned long long
#define M 1000010
using namespace std;
const int mod1 = 19260817;
const int mod2 = 19660813;
const int p=131;
/*================================================*/
ull n,ans=0;
string s;
struct node{
ull x,y;
}s1[M];
/*================================================*/
ull Hash1(string s)
{
int len=s.size();
ull tot=0;
for(int i=0;i<len;i++){
tot=((tot*p+(ull)s[i])%mod1+mod1)%mod1;
}
return tot;
}
ull Hash2(string s)
{
int len=s.size();
ull tot=0;
for(int i=0;i<len;i++){
tot=((tot*p+(ull)s[i])%mod2+mod2)%mod2;
}
return tot;
}
bool cmp(node a,node b)
{
return a.x<b.x;
}
/*=================================================*/
signed main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) {
cin>>s;
s1[i].x=Hash1(s);
s1[i].y=Hash2(s);
}
sort(s1+1,s1+n+1,cmp);
for(int i=1;i<=n;i++){
if(s1[i].x!=s1[i-1].x||s1[i].y!=s1[i-1].y) ans++;
}
cout<<ans;
return 0;
}
这就是一个双哈希的模板题目。
计算子串的哈希值
前缀哈希值和后缀哈希值的求法
如果我们已知字符串 \(S\) 的 \(Hash\) 值是 \(H(S)\) ,字符串 \(S + T\) 的 \(Hash\) 值是 \(H(S + T)\) ,那么字符串 \(T\) 的 \(Hash\) 值就是
根据这个性质就可以进行运算。
前缀 \(Hash\) 值
$$Hash[k] = Hash[i] - Hash[i - k] * power[k]$$
后缀 \(Hash\) 值
$$Hash[k] = Hash[i - k + 1] - Hash[i + 1] * power[k]$$
之后查询子串的时候就可以 \(O(1)\) 查询。
void prepare()//前后缀Hash值和进制。
{
po[0] = 1;
for(int i = 1;i <= n;i ++) {//进制
po[i] = po[i - 1] * p;
}
for(int i = 1;i <= n;i ++) {
Hash_z[i] = Hash_z[i - 1] * p + s[i];//前缀Hash值
}
for(int i = n;i >= 1;i --) {
Hash_f[i] = Hash_f[i + 1] * p + s[i];//后缀Hash值
}
return;
}
例题
题意请自己看题面。
这个题目就是一个查询子串的例目,先预处理出子串的哈希值,在判断前缀的哈希值是否等于后缀,得出答案。
#include<cstdio>
#include<iostream>
#include<vector>
#define ull unsigned long long
#define ll long long
#define M 1000010
using namespace std;
const int mod1 = 19260817;
const int mod2 = 19660813;
const int p = 31;
/*================================================*/
char s[M >> 1];
ll po[M];
ll Hash[M];
/*================================================*/
void prepare(int x)
{
po[0] = 1;
for(int i = 1;i <= N; i++) {
po[i] = po[i - 1] * p;
}
for(int i = 0;i < x; i++) {
Hash[i] = Hash[i - 1] * p + (ll)s[i];
}
return;
}
/*=================================================*/
signed main()
{
while(cin >> s) {
int len = strlen(s);
prepare(len);//计算出进制,计算Hash值
for(int i = 1;i <= len;i ++) {
int l = Hash[i - 1];
int r = Hash[len - 1] - Hash[len - i - 1] * po[i];
if(l == r) {
printf("%d ",i);
}
}
printf("\n");
}
return 0;
}
还有这道 link luogu 3498
这道题目前缀哈希值和后缀哈希值都用到了,也就是最多能分成多少个子串,如果,大于当前最大值就换掉,最后求得的结果就是最终答案。
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
#include<map>
#include<vector>
#include<set>
#define ull unsigned long long
#define ll long long
#define M 1000010
#define N 1010
#define INF 0x3f3f3f3f
using namespace std;
const int p = 10007;
/*================================================*/
int n;
int s[M];
ull Hash_z[M], Hash_f[M], po[M];;//正Hash值 ,反Hash值,进制
int cnt;//计算有几个最优解
int ans_cnt;//看可分为几段不同的值
vector<ull> qp;//储存每次分割的答案
int maxn = -1e5;//计算最终的可分的最大的段数
vector<int> ans;//储存每个最优解
int m; //剪枝用
/*================================================*/
inline int read()
{
int s = 0, f = 0;char ch = getchar();
while (!isdigit(ch)) f |= ch == '-', ch = getchar();
while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
return f ? -s : s;
}
void prepare()//前后缀Hash 值和进制位
{
po[0] = 1;
for(int i = 1;i <= n;i ++) {
po[i] = po[i - 1] * p;
}
for(int i = 1;i <= n;i ++) {
Hash_z[i] = Hash_z[i - 1] * p + s[i];
}
for(int i = n;i >= 1;i --) {
Hash_f[i] = Hash_f[i + 1] * p + s[i];
}
return;
}
bool check(int x)//判断函数,判断是否有这个子串
{
for(int i = 0;i <qp.size(); i ++) {
if(qp[i] == x) return false;
}
return true;
}
void solve(int k)
{
ans_cnt = 0;
for(int i = k;i <= n;i += k) {
int sum_z = Hash_z[i] - Hash_z[i - k] * po[k];
//这个子串前缀Hash值
int sum_f = Hash_f[i - k + 1] - Hash_f[i + 1] * po[k];//后缀
if(check(sum_z)) {//判断
qp.push_back(sum_z);
ans_cnt++;//累加可分的段数
//if(check(sum_f)) //剪枝 1 ,效果如上
qp.push_back(sum_f);
}
}
if(maxn == ans_cnt) {//当已知的最优解和新求出的解相同时
ans.push_back(k);//记录k 值
cnt++;//最优解个数++
} else if(maxn < ans_cnt) {//又新求出更优的解
ans.clear();//清空原来的答案序列
ans.push_back(k);//添加解
maxn = ans_cnt;
cnt = 1;
}
if(ans_cnt != 0) {
m = min(m,n / ans_cnt);//剪枝 2 效果如上
}
qp.clear();//多次分割记得清空
}
/*=================================================*/
signed main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = read();
for(int i = 1;i <= n;i ++) {
s[i] = read();
}
prepare();
m = n;
for(int i = 1;i <= m;i ++) solve(i);
printf("%d %d\n",maxn,cnt);
for(int i = 0;i <ans.size();i ++) printf("%d ",ans[i]);//输出
return 0;
}
这个题看不太懂的话去看 link。
总结
说一下我写字符串哈希出错的地方吧。
-
取进制数的时候取小了,使得程序冲突性太高,本来满分的程序被卡到了 \(72\) 分。
-
求子串的哈希值时写了个 \(power[1] = 0\) ,天知道我咋想的。
-
取模数时取了个合数。
-
枚举子串的哈希值时,左右区间取错,(常有的事)。
结束了$ \cdots $。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号