矩阵连乘问题

矩阵连乘问题详解（C++实现）

矩阵连乘问题是一个经典的动态规划问题，目标是找到一组矩阵相乘的最优顺序，使得计算所需的标量乘法次数最少。

问题描述

给定n个矩阵{A1, A2, ..., An}，其中矩阵Ai的维数为p[i-1]×p[i]，确定矩阵连乘积A1A2...An的计算顺序，使得计算该乘积所需的标量乘法次数最少。

动态规划解法思路

1. 最优子结构：问题的最优解包含子问题的最优解
2. 重叠子问题：递归算法会重复计算相同的子问题
3. 建立递推关系：
   • 定义m[i][j]为计算矩阵Ai到Aj的最小乘法次数
   • 递推公式：m[i][j] = min{m[i][k] + m[k+1][j] + p[i-1]p[k]p[j]} (i ≤ k < j)

C++代码实现

#include <iostream>
#include <vector>
#include <climits>
using namespace std;

// 打印最优括号化方案
void printOptimalParens(vector<vector<int>>& s, int i, int j) {
    if (i == j) {
        cout << "A" << i;
    } else {
        cout << "(";
        printOptimalParens(s, i, s[i][j]);
        printOptimalParens(s, s[i][j] + 1, j);
        cout << ")";
    }
}

// 矩阵连乘的动态规划算法
void matrixChainOrder(vector<int>& p) {
    int n = p.size() - 1; // 矩阵个数
    vector<vector<int>> m(n + 1, vector<int>(n + 1, 0)); // 存储最小乘法次数
    vector<vector<int>> s(n + 1, vector<int>(n + 1, 0)); // 存储分割点
    
    // l是链长度
    for (int l = 2; l <= n; l++) {
        for (int i = 1; i <= n - l + 1; i++) {
            int j = i + l - 1;
            m[i][j] = INT_MAX;
            
            // 尝试所有可能的分割点k
            for (int k = i; k < j; k++) {
                int cost = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                if (cost < m[i][j]) {
                    m[i][j] = cost;
                    s[i][j] = k; // 记录最优分割点
                }
            }
        }
    }
    
    cout << "最小乘法次数: " << m[1][n] << endl;
    cout << "最优括号化方案: ";
    printOptimalParens(s, 1, n);
    cout << endl;
}

int main() {
    // 示例：6个矩阵的维度分别为30×35, 35×15, 15×5, 5×10, 10×20, 20×25
    vector<int> p = {30, 35, 15, 5, 10, 20, 25};
    
    matrixChainOrder(p);
    
    return 0;
}

代码详细解析

1. 数据结构：

   • p数组：存储矩阵链的维度，第i个矩阵的维度为p[i-1]×p[i]
   • m矩阵：m[i][j]表示计算Ai到Aj的最小乘法次数
   • s矩阵：s[i][j]记录Ai到Aj的最优分割点k

2. 初始化：

   • 当i=j时，m[i][j]=0（单个矩阵不需要乘法）

3. 填充m和s矩阵：

   • 外层循环按链长度l从2到n递增
   • 内层循环遍历所有长度为l的子链
   • 对于每个子链，尝试所有可能的分割点k，计算对应的乘法次数

4. 最优解构造：

   • 通过递归打印s矩阵，构造最优括号化方案

时间复杂度分析

• 三重循环结构使时间复杂度为O(n³)
• 空间复杂度为O(n²)（用于存储m和s矩阵）

示例输出

对于输入p = {30, 35, 15, 5, 10, 20, 25}，程序输出：

最小乘法次数: 15125
最优括号化方案: ((A1(A2A3))((A4A5)A6)

这表示最优计算顺序是：(A1(A2A3))((A4A5)A6)，最少需要15125次标量乘法。

1141: 矩阵最优连乘问题

题面

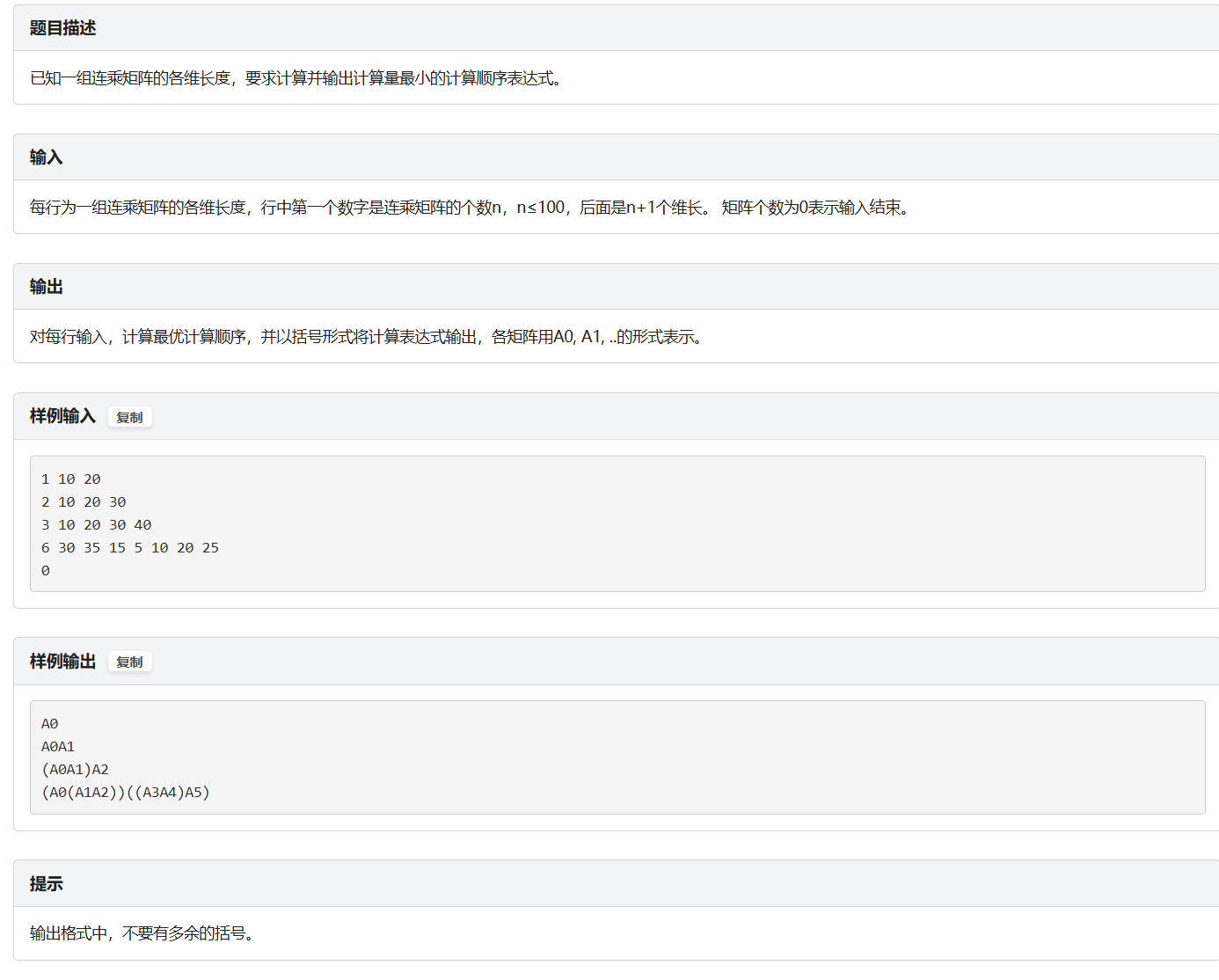
示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
//#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 2e5 + 2;
const int inf = 1e9;
const double eps = 1e-6;

void print(vector<vector<int>> &s, int i, int j, int n) {
    if(i == j) {
        cout << "A" << i - 1;
        return;
    }
    if(i != 1 || j != n) cout << '(';
    print(s, i, s[i][j], n);
    print(s, s[i][j] + 1, j, n);
    if(i != 1 || j != n) cout << ')';
}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);

    int n;
    while(cin >> n, n) {
        vector<int> p(n + 1);
        for(int i = 0; i <= n; ++i) cin >> p[i];
        vector<vector<int>> dp(n + 1, vector<int>(n + 1, inf));
        vector<vector<int>> s(n + 1, vector<int>(n + 1));
        // dp[i][j] 表示从i到j的最小乘法次数
        // s[i][j] 表示从i到j的最优分割点
        fer(i, 1, n + 1) {
            dp[i][i] = 0;
            s[i][i] = i;
        }
        fer(len, 2, n + 1) {
            for(int i = 1; i + len - 1 <= n; ++i) {
                int j = i + len - 1;
                fer(k, i, j) {
                    int cost = dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j];
                    if(cost < dp[i][j]) {
                        dp[i][j] = cost;
                        s[i][j] = k;
                    }
                }
            }
        }
        print(s, 1, n, n);
        cout << '\n';
    }

    return 0;
}