Contest3923 - 计科23级算法设计与分析上机作业-03

A.质数

题面

思路

考虑到输入数据量较大，选择线性欧拉筛预处理

示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
//#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 1e5 + 2;
const int inf = 1e9;

vector<bool> is_prime(N, true);
vector<int> primes;

void siebe() {
    is_prime[0] = is_prime[1] = false;
    fer(i, 2, N) {
        if(is_prime[i]) primes.push_back(i);
        for(int j = 0; j < primes.size() && i * primes[j] < N; ++j) {
            is_prime[i * primes[j]] = false;
            if(i % primes[j] == 0) break;
        }
    }
}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);

    siebe();
    int t;
    cin >> t;
    while(t--){
        int n;
        cin >> n;
        cout << (is_prime[n] ? "yes" : "no");
        cout << '\n';
    }

    return 0;
}

B.分治法求解全排列问题

题面

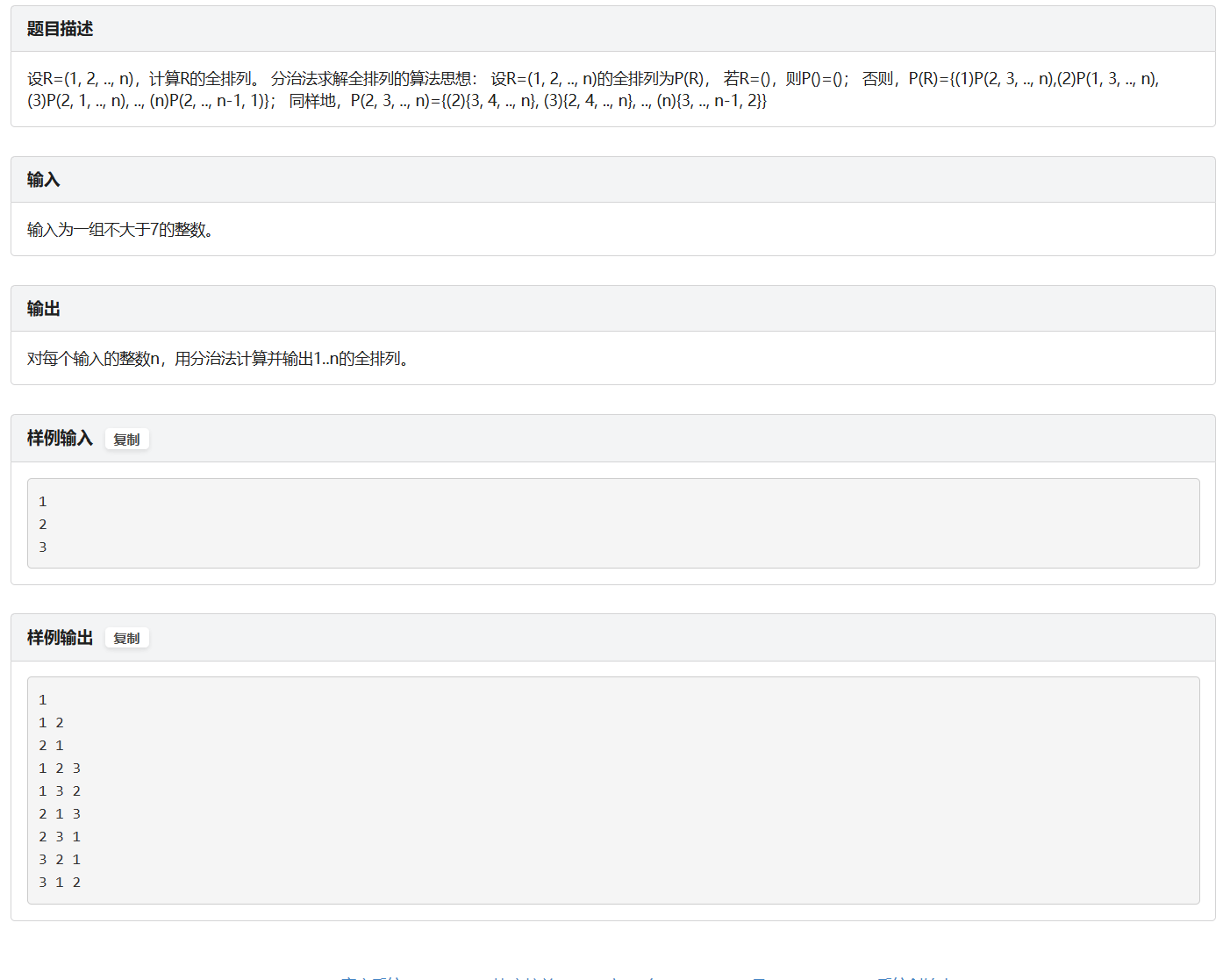
思路

分治法求全排列问题，注意输出的答案不兼容其他做法（如果是按字典序输出的做法不可行）

示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
//#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 2e5 + 2;
const int inf = 1e9;

void perm(int n, int l, int r, vector<int>& arr) {
    if(l == r) {
        fer(i, 0, n) cout << arr[i] << " ";
        cout << '\n';
        return;
    }
    for(int i = l; i <= r; ++i) {
        swap(arr[l], arr[i]);
        perm(n, l + 1, r, arr);
        swap(arr[l], arr[i]);
    }
}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);

    int n;
    while(cin >> n) {
        vector<int> arr(n);
        fer(i, 0, n) arr[i] = i + 1;
        perm(n, 0, n - 1, arr);
    }

    return 0;
}

C.数的计数

题面

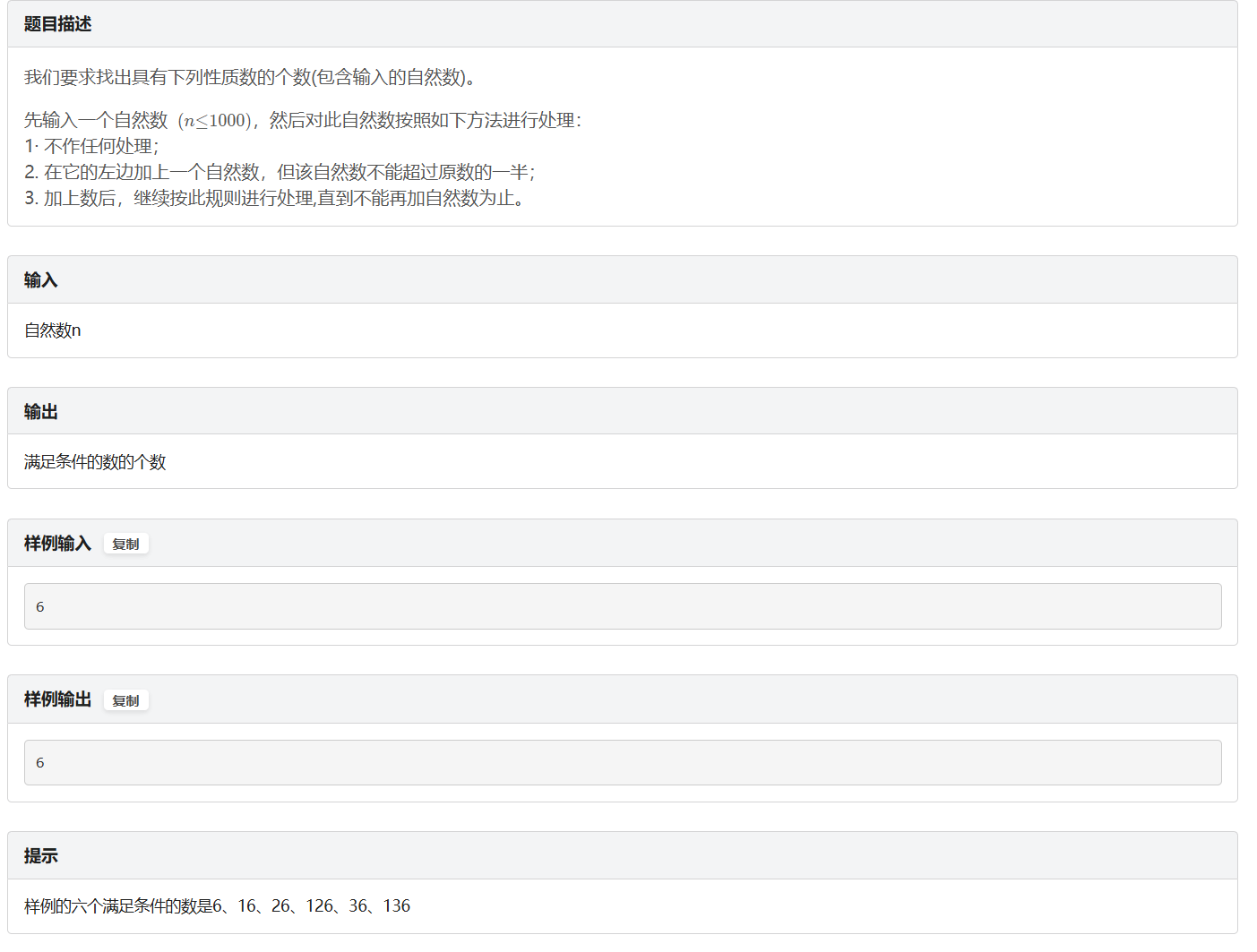
思路

递归处理，在处理过程中同时进行记忆化。

示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
//#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 1e3 + 2;
const int inf = 1e9;

vector<int> memo(N, -1);

int generateNumbers(int n) {
    if (n == 0) return 0;
    if (memo[n] != -1) return memo[n];

    int cnt = 1;
    for (int i = 1; i <= n / 2; ++i) cnt += generateNumbers(i);
    
    memo[n] = cnt;
    return cnt;
}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);

    int n;
    cin >> n;
    
    cout << generateNumbers(n) << '\n';

    return 0;
}

D.循环日程表问题，《算法竞赛入门经典》P230，递归与分治，刘丽萍，CCF三级

题面

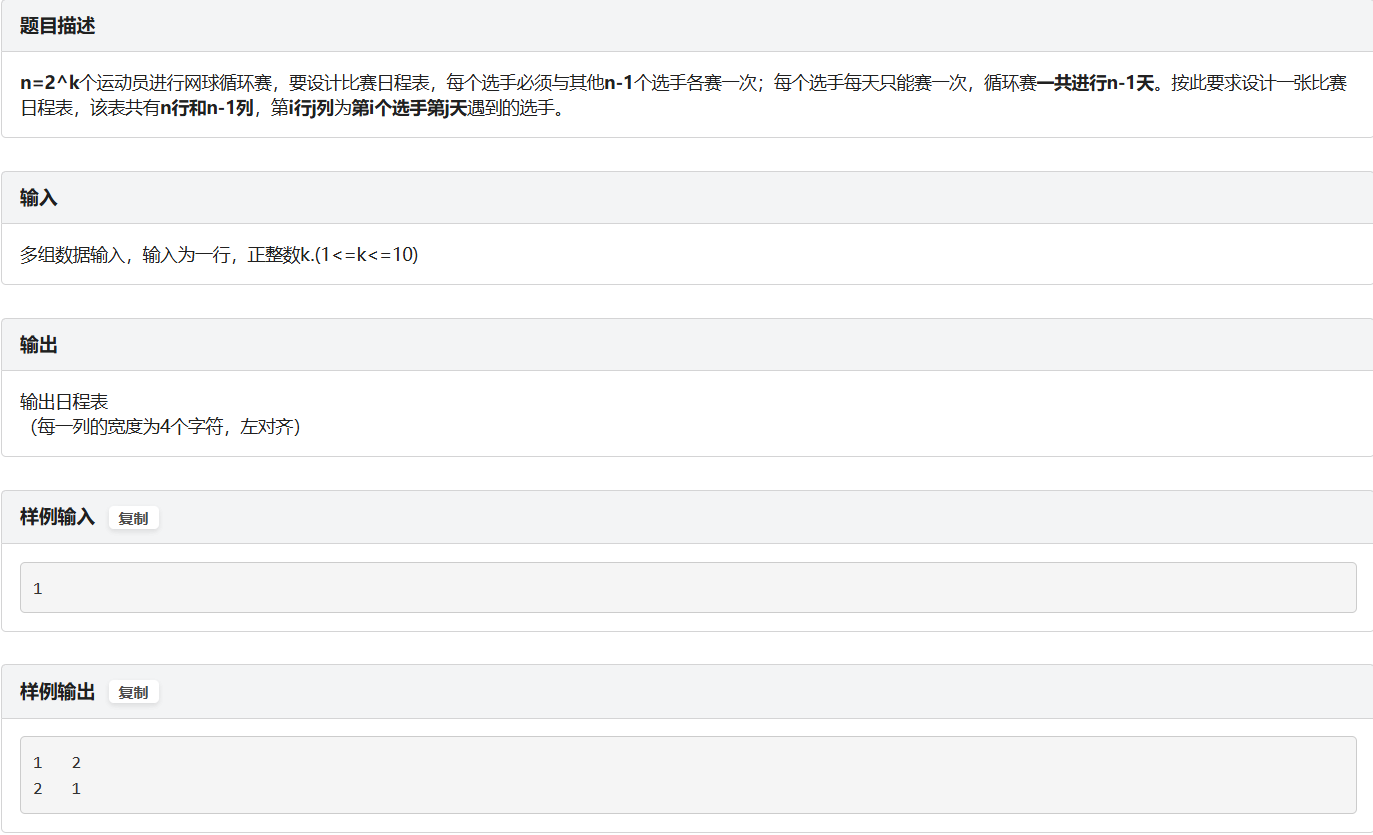
示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
//#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 2e5 + 2;
const int inf = 1e9;

void schedule(int k, int n, int** array);


int main()
{
    //ios::sync_with_stdio(false); cin.tie(nullptr);

    int k;
    while(cin >> k){
        int n = 1 << k;

        int** array = new int* [n+1];
        for (int i = 0;i < n+1;i++) array[i] = new int[n+1];

        schedule(k, n, array);
        
        for (int i = 1;i <= n;i++)
        {
            for (int j = 1;j <= n;j++)
                printf("%-4d", array[i][j]);
            cout << "\n";
        }
        
        for (int i = 0;i < n + 1;i++)
            delete[] array[i];
        delete[] array;
    }
    
    return 0;
}

void schedule(int k, int n, int** array)  
{
    for (int i = 1;i <= n;i++) array[1][i] = i;
    
    int m = 1;  
    
    for (int s = 1;s <= k;s++) 
    {
        n = n / 2;
        for (int t = 1;t <= n;t++)  // 第s部分内的循环
        {
            for (int i = m + 1;i <= 2 * m;i++) // 行
            {
                for (int j = m + 1;j <= 2 * m;j++) // 列
                {
                    array[i][j + (t - 1) * m * 2] = array[i - m][j + (t - 1) * m * 2 - m];       //左上角等于右下角的值
                    array[i][j + (t - 1) * m * 2 - m] = array[i - m][j + (t - 1) * m * 2];       //左下角等于右上角的值
                }

            }

        }
        m *= 2;
    }

}

E.求逆序对(deseq)

题面

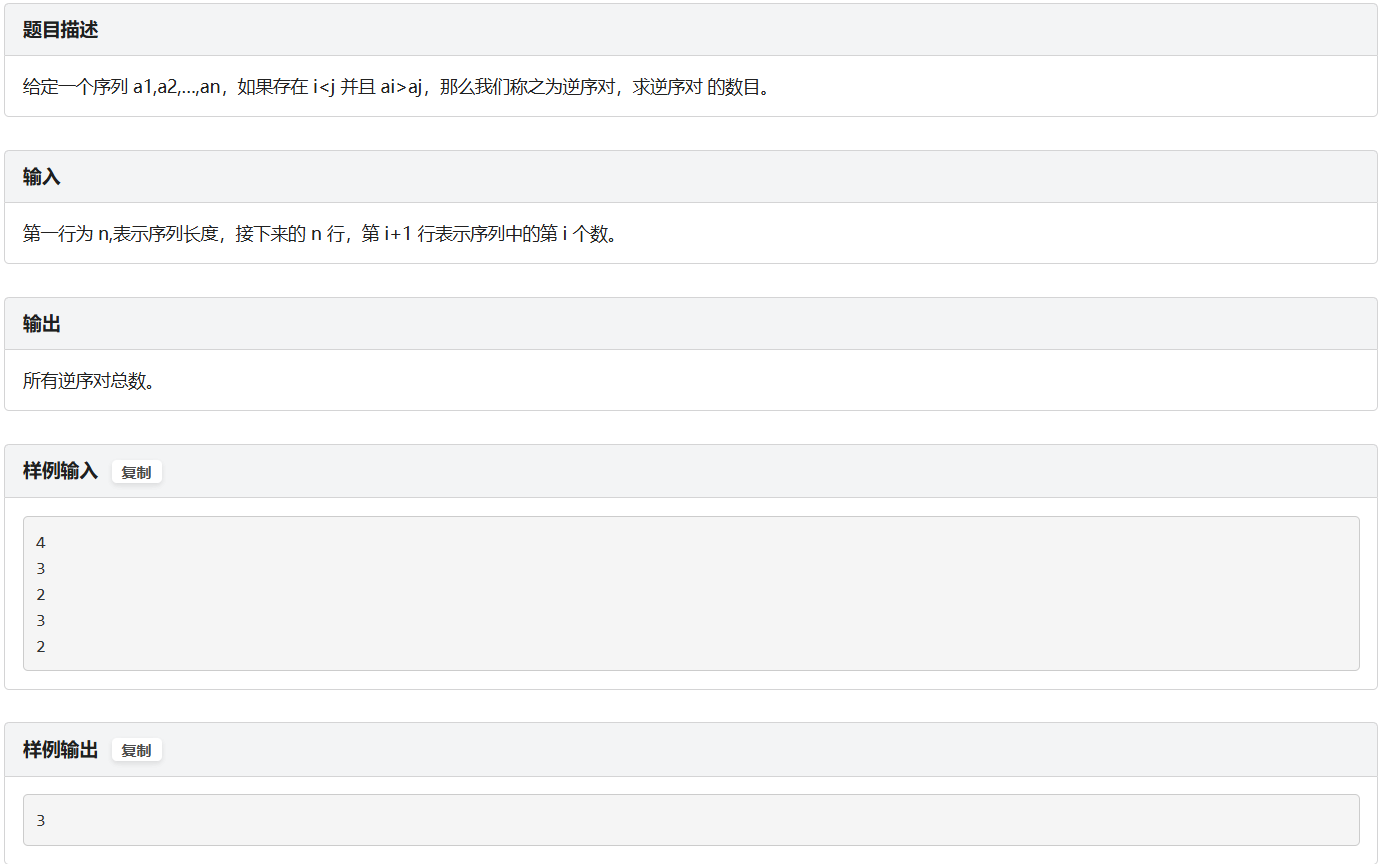
示例代码

#include <bits/stdc++.h>
using namespace std;
#define int long long

long long mergeAndCount(vector<int>& arr, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    vector<int> L(n1), R(n2);

    for (int i = 0; i < n1; ++i)
        L[i] = arr[left + i];
    for (int j = 0; j < n2; ++j)
        R[j] = arr[mid + 1 + j];

    int i = 0, j = 0, k = left, swaps = 0;

    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k++] = L[i++];
        } else {
            arr[k++] = R[j++];
            swaps += (mid + 1) - (left + i);
        }
    }

    while (i < n1) {
        arr[k++] = L[i++];
    }

    while (j < n2) {
        arr[k++] = R[j++];
    }

    return swaps;
}

int mergeSortAndCount(vector<int>& arr, int left, int right) {
    long long count = 0;
    if (left < right) {
        int mid = left + (right - left) / 2;

        count += mergeSortAndCount(arr, left, mid);
        count += mergeSortAndCount(arr, mid + 1, right);

        count += mergeAndCount(arr, left, mid, right);
    }
    return count;
}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);
    int n;
    cin >> n;
    vector<int> arr(n);
    for(int i = 0; i < n; ++i) {
        cin >> arr[i];
    }

    int result = mergeSortAndCount(arr, 0, n - 1);
    cout << result << endl;

    return 0;
}