8158: 最小公倍数的最小和（Minimum Sum LCM）

[题目链接](https://buctoj.com/problem.php?id=8158）

题面

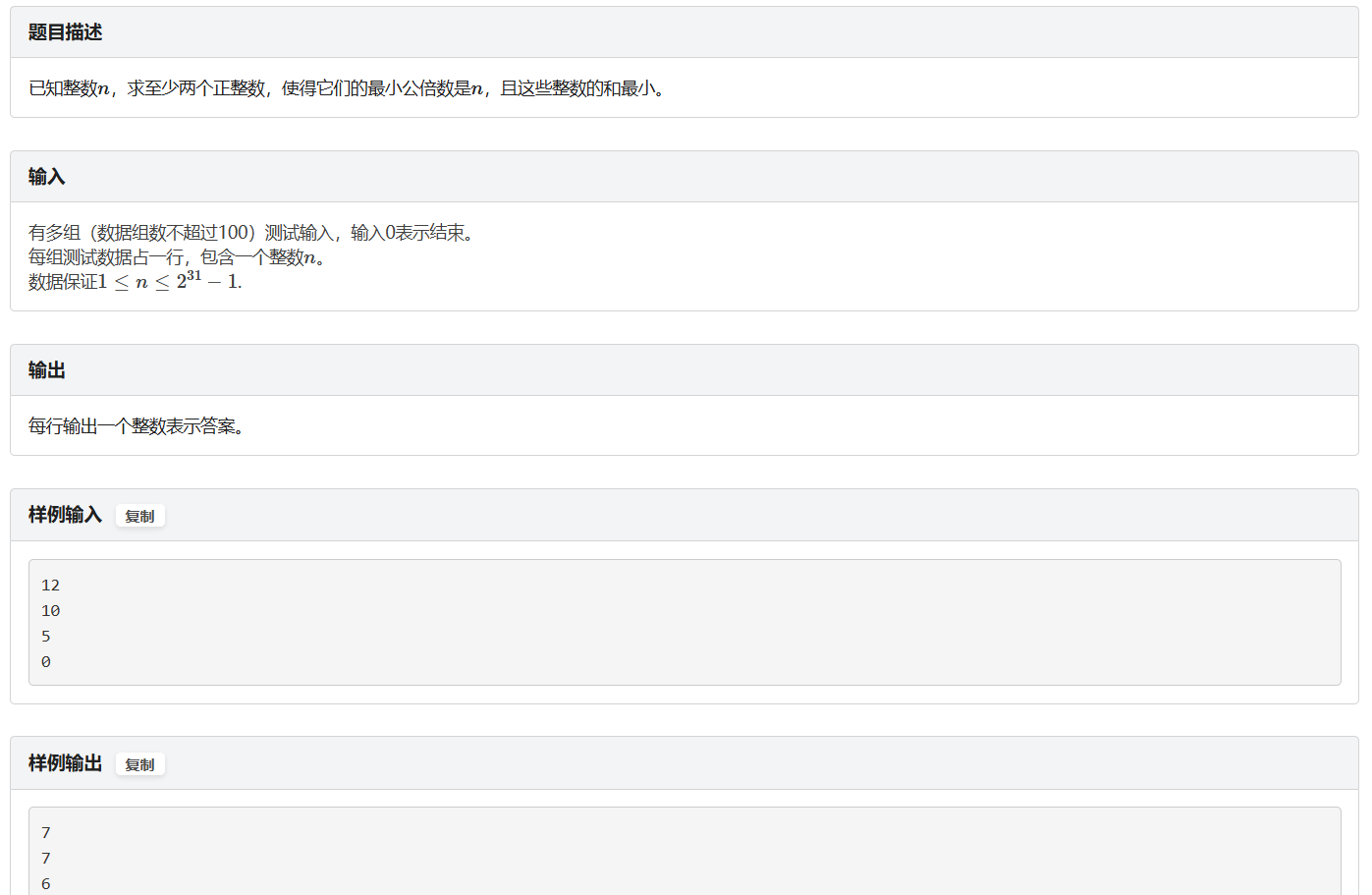
思路

根据数论知识，我们知道，一个大于等于2的整数均可以被拆分成有限个质数的乘积。也即当\(n >= 2\)时，有$n = $ \(p_1\)^\(a_1\) \(*\) \(p_2\)^\(a_2\) \(*...*\) \(p_n\)^\(a_n\)
那么如果我们将每一部分拿开来，它们的最小公倍数就是\(n\)，那如何使得它们的和最小呢？
我们可以特殊化，从简单的二维来讨论。易知\(m, n >= 2\)时，有\(m * n >= m + n\)。所以类比到多项的情况，我们可以猜测每个质因子\(p_i\)^\(a_i\)单独地存在于一个数字中，答案是最优的。

注意

当\(n == 1\)时，由于至少需要分为两项，所以\(n = 1 * n, ans = 1 + n\)
当n只有一个质因子时， $n = $ \(p_i\)^\(a_i\) \(* 1, ans = 1 +\) \(p_i\)^\(a_i\)

示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 2e5 + 2;
const int inf = 1e9;

int fpow(int a, int b){
    int ans = 1;
    while(b){
        if(b & 1) ans = ans * a;
        b >>= 1;
        a = a * a;
    }
    return ans;
}

bool is_prime(int x){
    if(x < 2) return false;
    for(int i = 2; i <= x / i; i++){
        if(x % i == 0) return false;
    }
    return true;
}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);

    int n, t = 1, st= 0;
    while(cin >> n, n){
        if(n == 1) {cout << 2 << '\n'; continue;}
        //if(is_prime(n)) {cout << 1 + n << '\n'; continue;}
        ll ans = 0;
        set<int> st;
        for(int i = 2; i <= n / i; ++i){
            int cnt = 0;
            while(n % i == 0){
                cnt++;
                st.insert(i);
                n /= i;
            }
            ans += (cnt ? fpow(i, cnt) : 0);
        }
        if(n > 1) ans += n, st.insert(n);
        if(st.size() == 1) ans += 1;
        cout << ans << '\n';
    }

    return 0;
}