8159: GCD等于XOR（GCD XOR）

题目链接

题面

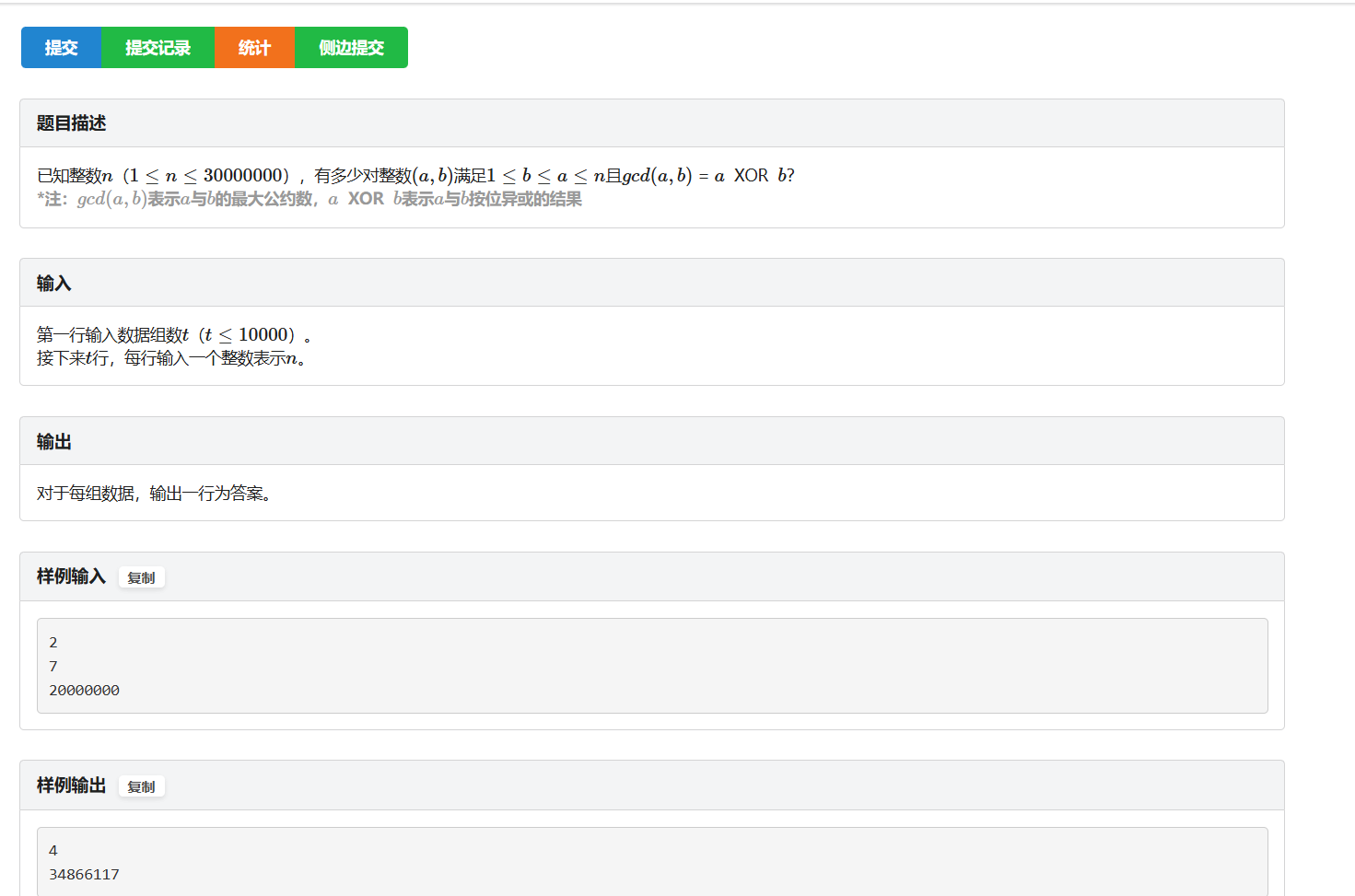
思路

1. 首先需要掌握异或的几个性质：
   ① 若\(a \oplus b = c\) <=> \(a \oplus c = b\)
   ② 异或运算是两个数在二进制表示下不进位的加法，于是就有\(a - b <= a \oplus b <= a + b\)
2. 分析此题，因为a, b 均是 gcd(a, b) 的倍数，所以就有 a - b = kgcd(a, b)(同余的性质），并且a - b >= gcd(a, b)。而根据上面异或的性质，异或是不进位的加法，也即\(a - b <= a \oplus b = gcd(a, b)\)。综上所述，得出\(a - b = gcd(a, b) = a \oplus b\)
3. 根据上面的结论我们应该有思路了，我们可以枚举 x 和 y ，但是这样时间复杂度较高。我们可以换一种枚举方法，我们可以先枚举gcd(a, b), 它的范围一定不超过 (N >> 1) + 1，然后在枚举x，它一定是gcd(a, b) 的倍数， 所以可以倍增枚举，这样的话时间复杂度大概就是$$nlogn$$，可以满足题目要求。

注意

如果将示例代码中的if(x - g == (x ^ g)) f[x]++;写成f[x] += x - g == (x ^ g)会TLE

示例代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
//#define int ll
#define pii pair<int, int>
#define all(x) x.begin(),x.end()
#define fer(i, m, n) for(int i = m; i < n; ++i)
#define ferd(i, m, n) for(int i = m; i >= n; --i)
#define dbg(x) cout << #x << ' ' << char(61) << ' ' << x << '\n'

const int MOD = 1e9 + 7;
const int N = 3e7;
const int inf = 1e9;

int f[N];

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);

    int t;
    scanf("%d", &t);

    fer(g, 1, (N >> 1) + 1){
        for(int x = g << 1; x <= N; x += g)
            if(x - g == (x ^ g)) f[x]++;
    }
    fer(i, 1, N + 1) f[i] += f[i - 1];

    while(t--){
        int n;
        scanf("%d", &n);
        printf("%d\n", f[n]);
    }
    return 0;
}