机器学习—降维-特征选择6-4（PCA-Kernel方法）

使用PCA核方法对糖尿病数据集降维

主要步骤流程：

• 1. 导入包
• 2. 导入数据集
• 3. 数据预处理
  • 3.1 检测缺失值
  • 3.2 生成自变量和因变量
  • 3.3 拆分训练集和测试集
  • 3.4 特征缩放
• 4. 使用 Kernel PCA 降维
• 5. 构建逻辑回归模型
  • 5.1 使用原始数据构建逻辑回归模型
  • 5.2 使用降维后数据构建逻辑回归模型
• 6. 可视化Kernel PCA 降维效果

 

数据集链接：https://www.cnblogs.com/ojbtospark/p/16014512.html

 

1. 导入包

In [2]:

# 导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

 

2. 导入数据集

In [3]:

# 导入数据集
dataset = pd.read_csv('pima-indians-diabetes.csv')
dataset

Out[3]:

	preg	plas	pres	skin	test	mass	pedi	age	class
0	6	148	72	35	0	33.6	0.627	50	1
1	1	85	66	29	0	26.6	0.351	31	0
2	8	183	64	0	0	23.3	0.672	32	1
3	1	89	66	23	94	28.1	0.167	21	0
4	0	137	40	35	168	43.1	2.288	33	1
...	...	...	...	...	...	...	...	...	...
763	10	101	76	48	180	32.9	0.171	63	0
764	2	122	70	27	0	36.8	0.340	27	0
765	5	121	72	23	112	26.2	0.245	30	0
766	1	126	60	0	0	30.1	0.349	47	1
767	1	93	70	31	0	30.4	0.315	23	0

768 rows × 9 columns

 

3. 数据预处理

3.1 检测缺失值

In [4]:

# 检测缺失值
null_df = dataset.isnull().sum()
null_df

Out[4]:

preg     0
plas     0
pres     0
skin     0
test     0
mass     0
pedi     0
age      0
class    0
dtype: int64

3.2 生成自变量和因变量

In [5]:

# 生成自变量和因变量
X = dataset.iloc[:,0:8].values
y = dataset.iloc[:,8].values

3.3 拆分训练集和测试集

In [6]:

# 拆分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                test_size = 0.2, random_state = 1)

print(X_train.shape)

(614, 8)

3.4 特征缩放

In [7]:

# 特征缩放
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)

 

4. 使用 Kernel PCA 降维

In [128]:

# 使用 Kernel PCA 生成新的自变量
from sklearn.decomposition import KernelPCA
kernel_pca = KernelPCA(n_components = 3, kernel='sigmoid') 
X_train_kernel_pca = kernel_pca.fit_transform(X_train)
print(X_train_kernel_pca)

[[ 0.53677552  0.18237473 -0.06784237]
 [ 0.2525542   0.21315067 -0.10500243]
 [ 0.22619011  0.14259737 -0.28290242]
 ...
 [ 0.22015692  0.56336814 -0.19225494]
 [ 0.13823718  0.09177124  0.10862359]
 [ 0.15799345  0.26629945 -0.14812701]]

In [129]:

X_test_kernel_pca = kernel_pca.transform(X_test)

n_components的值需要不断尝试

 

5. 构建逻辑回归模型

5.1 使用原始数据构建逻辑回归模型

In [130]:

# 构建模型
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(penalty='l2', C=1, 
                                class_weight='balanced', random_state = 0)
classifier.fit(X_train, y_train)

Out[130]:

LogisticRegression(C=1, class_weight='balanced', random_state=0)

In [131]:

# 预测测试集
y_pred = classifier.predict(X_test)

In [132]:

# 评估模型性能
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))

0.7922077922077922

5.2 使用降维后数据构建逻辑回归模型

In [133]:

# 构建模型
classifier = LogisticRegression(penalty='l2', C=1, 
                                class_weight='balanced', random_state = 0)
classifier.fit(X_train_kernel_pca, y_train)

Out[133]:

LogisticRegression(C=1, class_weight='balanced', random_state=0)

In [134]:

# 预测测试集
y_pred = classifier.predict(X_test_kernel_pca)

In [135]:

# 评估模型性能
print(accuracy_score(y_test, y_pred))

0.7727272727272727

In [137]:

import seaborn as sns
ne=pd.concat([pd.DataFrame(X_train_kernel_pca),
              pd.DataFrame(y_train)],axis=1).reset_index(drop=True)
ne.columns = ['a', 'b', 'c', 'd']#, 'e','f','g','h']
antV = ['#1890FF', '#2FC25B']
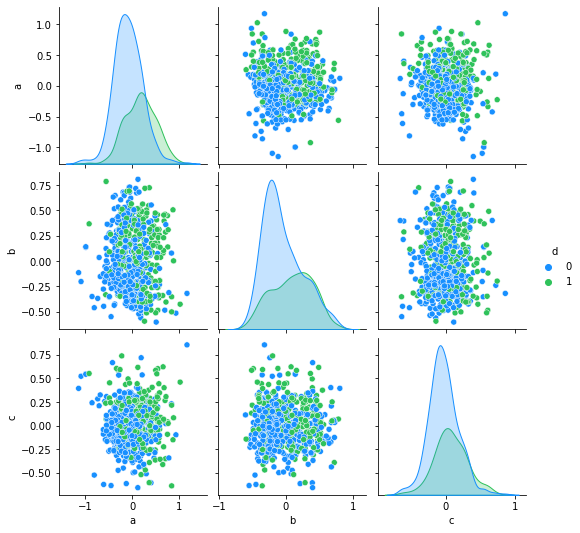
sns.pairplot(ne,palette=antV,hue='d')

Out[137]:

<seaborn.axisgrid.PairGrid at 0x1ff388dc250>

 

 

6. 可视化Kernel PCA 降维效果

In [138]:

from matplotlib.colors import ListedColormap
X_set, y_set = X_train_kernel_pca, y_train
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                color = ListedColormap(('red', 'green'))(i), label = j)
plt.title('PCA Viz')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()

 

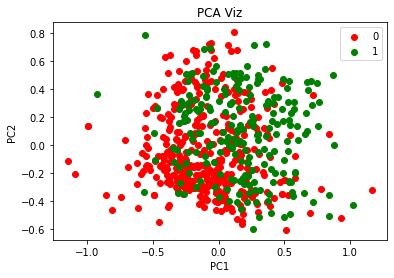
经过Kernel PCA降维，自变量由8个变为2个。

将降维后的2个主成分可视化，可以看到，如果以2个主成分训练逻辑回归模型，模型性能会较差，因为肉眼可见，2个类别之间没有明显的界限。