bzoj千题计划108:bzoj1018: [SHOI2008]堵塞的交通traffic
http://www.lydsy.com/JudgeOnline/problem.php?id=1018
关键点在于只有两行
所以一个2*m矩形连通情况只有6种
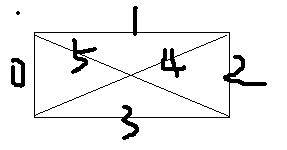
编号即对应代码中的a数组
线段树维护
用b数组表示 节点第0/1行的最右一列是否连接了右边
来 辅助 节点的合并
查询
对两个点位于矩形的位置分4种情况讨论
两点是否联通,要考虑四种情况
(以两个位置是矩形左上角和右上角为例)
1、直接联通,线段树的节点包含了这种情况,直接判断

2、
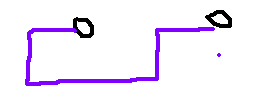
3、

4、

后三种情况需要再查询[1,l]和[r,n]的再合并
边界的处理:
(叶子节点只有一列)
只有一列的状态1和3 全部是true
如果是竖着联通,同时更新状态0和2,4和5
如果是横着联通,
第1行,如果最后一列可以往外合并,更新状态5
第2行,如果最后一列可以往外合并,更新状态4
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define ok { puts("Y"); continue; } using namespace std; #define N 100001 int L[N<<2],R[N<<2]; struct node { bool a[6],b[2]; void clear() { memset(a,false,sizeof(a)); memset(b,false,sizeof(b)); } node operator + (node p) const { node tmp; tmp.clear(); tmp.a[0]=a[0]; tmp.a[0]|=a[1]&&a[3]&&b[0]&&b[1]&&p.a[0]; // cout<<tmp.a[0]; tmp.a[1]=a[1]&&b[0]&&p.a[1]; tmp.a[1]|=a[5]&&b[1]&&p.a[4]; // cout<<tmp.a[1]; tmp.a[2]=p.a[2]; tmp.a[2]|=p.a[1]&&p.a[3]&&b[0]&&b[1]&&a[2]; // cout<<tmp.a[2]; tmp.a[3]=a[3]&&b[1]&&p.a[3]; tmp.a[3]|=a[4]&&b[0]&&p.a[5]; // cout<<tmp.a[3]; tmp.a[4]=a[4]&&b[0]&&p.a[1]; tmp.a[4]|=a[3]&&b[1]&&p.a[4]; // cout<<tmp.a[4]; tmp.a[5]=a[1]&&b[0]&&p.a[5]; tmp.a[5]|=a[5]&&b[1]&&p.a[3]; // cout<<tmp.a[5]; tmp.b[0]=p.b[0]; tmp.b[1]=p.b[1]; return tmp; } }; node tr[N<<2]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void build(int k,int l,int r) { L[k]=l; R[k]=r; if(l==r) { tr[k].a[1]=tr[k].a[3]=true; return; } int mid=l+r>>1; build(k<<1,l,mid); build(k<<1|1,mid+1,r); } void change(int k,int pos,bool ty,int line,bool how) { if(L[k]==R[k]) { if(!ty) { if(line==1) { tr[k].b[0]=how; if(tr[k].b[0] && tr[k].a[0]) tr[k].a[5]=true; else if(!tr[k].a[0]) tr[k].a[5]=false; } else { tr[k].b[1]=how; if(tr[k].b[1] && tr[k].a[0]) tr[k].a[4]=true; else if(!tr[k].a[0]) tr[k].a[4]=false; } } else { tr[k].a[0]=tr[k].a[2]=how; tr[k].a[4]=tr[k].a[5]=how; } return; } int mid=L[k]+R[k]>>1; if(pos<=mid) change(k<<1,pos,ty,line,how); else change(k<<1|1,pos,ty,line,how); tr[k]=tr[k<<1]+tr[k<<1|1]; } node query(int k,int l,int r) { if(L[k]>=l && R[k]<=r) return tr[k]; int mid=L[k]+R[k]>>1; if(r<=mid) return query(k<<1,l,r); if(l>mid) return query(k<<1|1,l,r); node ll=query(k<<1,l,r),rr=query(k<<1|1,l,r); return ll+rr; } int main() { // freopen("bzoj_1018.in","r",stdin); // freopen("bzoj_1018.out","w",stdout); int n; read(n); build(1,1,n); char c[7]; int lx,ly,rx,ry; int cnt=0; while(scanf("%s",c)!=EOF) { if(c[0]=='E') return 0; read(lx); read(ly); read(rx); read(ry); if(ly>ry) swap(lx,rx),swap(ly,ry); if(c[0]=='O' || c[0]=='C') { if(lx==rx) change(1,ly,0,lx,c[0]=='O'); else change(1,ly,1,lx,c[0]=='O'); } else { node tmp=query(1,ly,ry); if(ly==ry && tmp.a[0]) ok else if(ly!=ry) { if(lx==1 && rx==1 && tmp.a[1]) ok if(lx==2 && rx==2 && tmp.a[3]) ok if(lx==1 && rx==2 && tmp.a[5]) ok if(lx==2 && rx==1 && tmp.a[4]) ok } node l=query(1,1,ly); node r=query(1,ry,n); if(lx==1 && rx==1) { if(l.a[2]&&tmp.a[4]) ok if(r.a[0]&&tmp.a[5]) ok if(l.a[2]&&r.a[0]&&tmp.a[3]) ok } else if(lx==1 && rx==2) { if(l.a[2]&&tmp.a[3]) ok if(r.a[0]&&tmp.a[1]) ok if(l.a[2]&&r.a[0]&&tmp.a[4]) ok } else if(lx==2 && rx==1) { if(l.a[2]&&tmp.a[1]) ok if(r.a[0]&&tmp.a[3]) ok if(l.a[2]&&r.a[0]&&tmp.a[5]) ok } else { if(l.a[2]&&tmp.a[5]) ok if(r.a[0]&&tmp.a[4]) ok if(l.a[2]&&r.a[0]&&tmp.a[1]) ok } puts("N"); } } }
1018: [SHOI2008]堵塞的交通traffic
Time Limit: 3 Sec Memory Limit: 162 MBSubmit: 3852 Solved: 1265
[Submit][Status][Discuss]
Description
有一天,由于某种穿越现象作用,你来到了传说中的小人国。小人国的布局非常奇特,整个国家的交通系统可
以被看成是一个2行C列的矩形网格,网格上的每个点代表一个城市,相邻的城市之间有一条道路,所以总共有2C个
城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞,两座城市之间的道路会变得不连通,
直到拥堵解决,道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事,部长听说你来自一个科技高度
发达的世界,喜出望外地要求你编写一个查询应答系统,以挽救已经病入膏肓的小人国交通系统。 小人国的交通
部将提供一些交通信息给你,你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式:
Close r1 c1 r2 c2:相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了;Open r1 c1 r2 c2:相邻的两座城
市(r1,c1)和(r2,c2)之间的道路被疏通了;Ask r1 c1 r2 c2:询问城市(r1,c1)和(r2,c2)是否连通。如果存在一
条路径使得这两条城市连通,则返回Y,否则返回N;
Input
第一行只有一个整数C,表示网格的列数。接下来若干行,每行为一条交通信息,以单独的一行“Exit”作为
结束。我们假设在一开始所有的道路都是堵塞的。我们保证 C小于等于100000,信息条数小于等于100000。
Output
对于每个查询,输出一个“Y”或“N”。
Sample Input
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit
Sample Output
N


 浙公网安备 33010602011771号
浙公网安备 33010602011771号