icpc2018南京 M Mediocre String Problem（exkmp+mamacher）

题意：

给出2个串s和t

要求从s中选出连续一段区间[i,j]，拼接上t的前k个字符是回文串

且区间[i,j]长度要大于k

问三元组（i，j，k）有多少种

 

s中选出的区间长度要大于t的前缀，且要拼接出来是回文串

等价于

s选出的区间中，后一块是自回文的，前一块拼上t的前缀是回文串

等价于

s选出的区间中，后一块是自回文的，前一块的反串等于t的前缀

如图所示

 

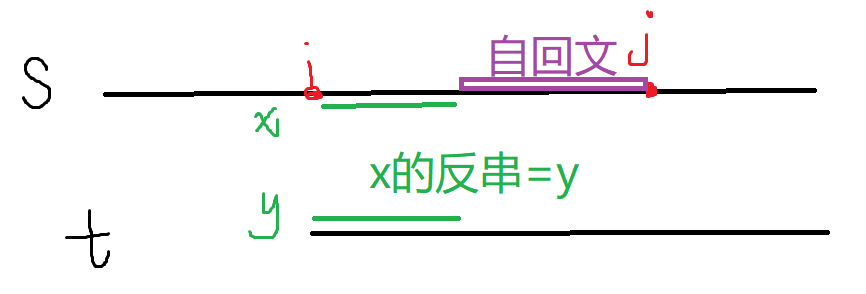
假设我们求出了s的所有回文串，并且可以枚举每个回文串位置

 我们枚举一个回文串位置

那么区间[i,j]除去自回文剩下的前一块，有多少个后缀的反串和t的前缀匹配，这就是s的这个回文串的贡献

s一个区间后缀的反串和t的前缀匹配

等价于

s的反串上，对应区间后缀和t的前缀匹配

所对应的贡献就是最长匹配长度

这个可以用exkmp求

 

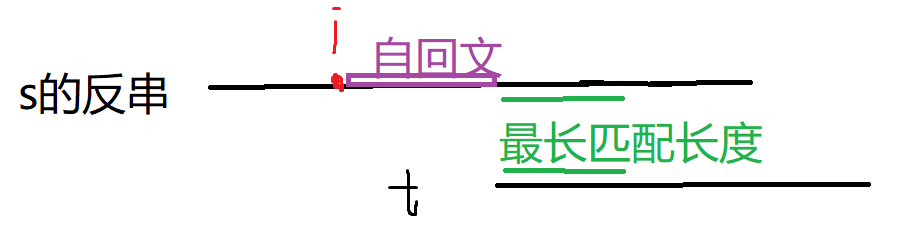
枚举回文串位置是不行的

我们可以先用mamacher求出每个位置的最长回文半径

回文半径覆盖的所有位置都有他们对应的最长匹配长度额贡献

把exkmp求出的extend数组做前缀和，就可以快速求一个s的一个回文中心对应的所有自回文串的所有贡献 

 

#include<bits/stdc++.h>

using namespace std;

#define N 1000004

char s[N],t[N];
char ss[N<<1];

int ls,lt;
int lss;

int extend[N],nxt[N]; 
long long suf[N];

int p[N<<1];

void getnext()
{
    int a=0,p,l,j;
    nxt[0]=lt;
    while(a<lt-1 && t[a]==t[a+1]) ++a;
    nxt[1]=a;
    a=1;
    for(int k=2;k<lt;++k)
    {
        p=a+nxt[a]-1;
        l=nxt[k-a];
        if(k-1+l>=p)
        {
            j=p-k+1>0 ? p-k+1 : 0;
            while(k+j<lt && t[k+j]==t[j]) ++j;
            nxt[k]=j;
            a=k;
        }
        else nxt[k]=l;
    }
}

void exkmp()
{
    getnext();
    int a=0;
    int minlen=ls<lt ? ls : lt;
    while(a<minlen && s[a]==t[a]) ++a;
    extend[0]=a;
    a=0;
    int p,l,j;
    for(int k=1;k<ls;++k)
    {
        p=a+extend[a]-1;
        l=nxt[k-a];
        if(k-1+l>=p)
        {
            j=p-k+1>0 ? p-k+1 : 0;
            while(k+j<ls && j<lt && s[k+j]==t[j]) ++j;
            extend[k]=j;
            a=k;
        }
        else extend[k]=l;
    }
    suf[0]=extend[0];
    for(int i=1;i<ls;++i) suf[i]=suf[i-1]+extend[i];
}

void manacher()
{
    ss[0]='!';
    for(int i=0;i<ls;++i)
    {
        ss[++lss]='#';
        ss[++lss]=s[i];
    }
    ss[++lss]='#';
    ss[lss+1]='@';
    int id=0,pos=0,x=0;
    for(int i=1;i<=lss;++i)
    {
        if(pos>i) x=min(p[id*2-i],pos-i);
        else x=1;
        while(ss[i-x]==ss[i+x]) ++x;
        if(i+x>pos) pos=i+x,id=i;
        p[i]=x;
    }
}

void solve()
{
    long long ans=0;
    int r,ql,qr;
    for(int i=2;i<=lss-2;++i)
    {
        r=p[i]-1>>1;
        if((i&1) && !r) continue;
        if(i&1) 
        {
            ql=i/2+1;
            qr=ql+r-1;
        }
        else 
        {
            ql=i/2;
            qr=ql+r;
        }
        if(qr==ls) --qr;
        ans+=suf[qr]-suf[ql-1];    
    }
    printf("%lld",ans);
}

int main()
{
    scanf("%s%s",s,t);
    ls=strlen(s);
    lt=strlen(t);
    reverse(s,s+ls);
    exkmp();
    manacher();
    solve();
}