算法分析 | 动态规划 | 字符串编辑距离

一.问题分析

将字符串s1 → s2需要的操作次数
s1:aaa_ _
s2:aaaab
①插入a  ②插入b,   所以dis=2

 

1.确定最优子结构

设d [ i ] [ j ] 是

串 { x1,x2,....., xi }

和

串 { y1,y2,....., yj }

的最短编辑距离.

无论两个字符串如何对齐,右侧只有3种对齐方式:

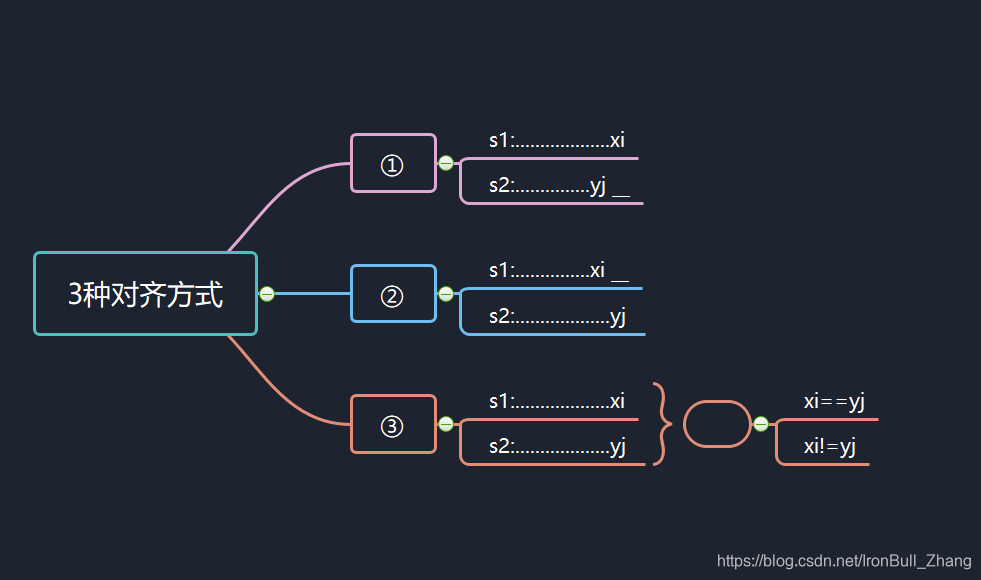
①:可看作串 { x1,x2,....., xi-1 }和串 { y1,y2,....., yj }的最优解 + 对s1删除1次xi

即 d [ i ] [ j ] = d [ i - 1 ][ j ] + 1 .

 

②:可看作串 { x1,x2,....., xi }和串 { y1,y2,....., yj-1 }的最优解 + 对s1添加1次yj

即 d [ i ] [ j ] = d [ i ][ j-1 ] + 1 .

 

③:s { x1,x2,....., xi-1 }和串 { y1,y2,....., yj-1 }的最优解+diff ( xi,yj ) 

即 d [ i ] [ j ] = d [ i-1 ][ j-1 ] + diff()

因此,我们得到

2.递归表达式:

d [ i ] [ j ] = min ( [ i - 1 ][ j ] + 1 ,d [ i ][ j-1 ] + 1 ,d [ i-1 ][ j-1 ] + diff ( xi,yj ) )

 

3.计算最优值

二维数组d[m][n]如下:

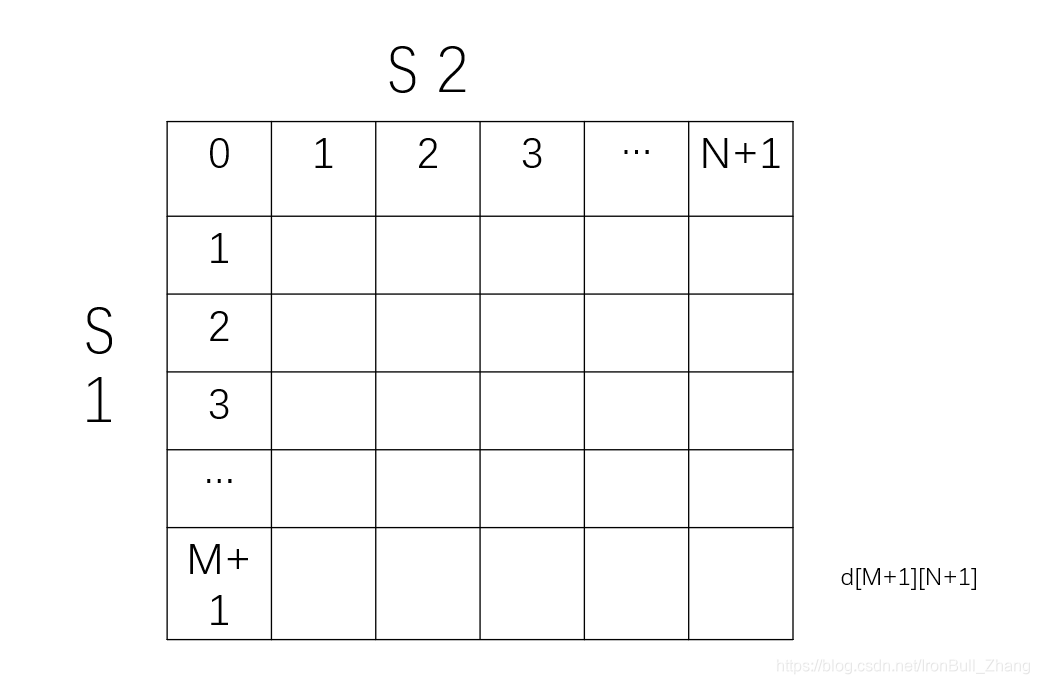
Q:为什么图中第一行和第一列的值不是默认的0,而是0,1,2,3.......呢?

A:d[0][j]表示空串s1和有 j 个字符的s2的编辑距离,举个例子:

s1:_ _ _ 

s2:a b c 

s1需要3次添加操作,故d[0][3]=3.

 

二.代码实现

1.EditDis.h

//确定两个字符是否相同
int diff(char a, char b)
{
	return a == b ? 0 : 1;
	
}

//可接受3个形参的min()重载
int min(int left, int up, int diff)
{
	return min(min(up, left), diff);
}

//编辑距离部分
int EditDis(string s1, string s2)
{
	//初始化部分
	int m = s1.length();
	int n = s2.length();
	int** d;
	d = new int*[m+1]; //这么做是为了让d[0][j]==0和d[i][0]==0,表示"当一个字符串为空时,与另一个字符串的修改距离为0"
	for (int i = 0; i <= m; i++)
	{
		d[i] = new int[n+1]();//添加(),得到初始值
	}
	
	//s1和空串比,需要删除的次数
	for (int i = 1; i <= m; i++)
	{
		d[i][0] = i;
	}

	//空串和s2比,需要添加的次数
	for (int j = 1; j < n; j++)
	{
		d[0][j] = j;
	}

	//开始动态规划
	for (int i = 1; i <= m; i++)
	{
		for (int j = 1; j <=  n; j++)
		{
			//s1的右端比s2的右端多一个
			//s1的右端比s2的右端多一个
			//s1的右端与s2的右端对齐+(0:xi==yj; 1:xi!=yj)
			d[i][j] = min(d[i - 1][j] + 1, d[i][j - 1] + 1, d[i - 1][j - 1] + diff(s1[i - 1], s2[j - 1]));
		} 
	}
	int ans = d[m][n];


	//释放new的内存空间
	for (int i = 0; i <= m; i++)
	{
		delete[] d[i];//得到初始值全==0的二维数组
	}
	delete[] d;

	return ans;

}

2.main()部分

	string s1, s2;
	cout << "输入字符串s1:\t"; cin >> s1;
	cout << "输入字符串s2:\t"; cin >> s2;
	cout << s1 << endl << s2 << endl;
	cout << "编辑距离为:\t" << EditDis(s1, s2);

但是只能给出编辑的距离,编辑路径如何显示?

3.辅助数组

修改后的相关函数void EditDis()、void EDPrint();

​int ccc[50][50];//辅助数组**c是在函数里定义的局部变量,不能被EDPrint()调用

int EditDis(string s1, string s2)
{
	//初始化部分
	int m = s1.length(); 
	int n = s2.length(); 
	
	int** d = new int*[m+1]; //这么做是为了让d[0][j]==0和d[i][0]==0,表示"当一个字符串为空时,与另一个字符串的修改距离为0"
	int** c = new int* [m + 1];
	for (int i = 0; i <= m; i++)
	{
		d[i] = new int[n+1]();//添加(),得到初始值
		c[i] = new int[n + 1]();
	}
	
	//s1和空串比,需要删除的次数
	for (int i = 1; i <= m; i++)
	{
		d[i][0] = i;
	}

	//空串和s2比,需要添加的次数
	for (int j = 1; j < n; j++)
	{
		d[0][j] = j;
	}

	//开始动态规划
	for (int i = 1; i <= m; i++)
	{
		for (int j = 1; j <=  n; j++)
		{
			//s1的右端比s2的右端多一个
			//s1的右端比s2的右端多一个
			//s1的右端与s2的右端对齐+(0:xi==yj; 1:xi!=yj)
			d[i][j] = min(d[i - 1][j] + 1, d[i][j - 1] + 1, d[i - 1][j - 1] + diff(s1[i - 1], s2[j - 1]));

			if (d[i - 1][j - 1] + diff(s1[i - 1], s2[j - 1]) < (d[i - 1][j] + 1 && d[i - 1][j - 1] + diff(s1[i - 1], s2[j - 1]) < d[i][j - 1] + 1))
			{
				if (diff(s1[i - 1], s2[j - 1]))
				{
					c[i][j] = 1;//源于左s上方,修改过则赋1,对s1 xi→yj,未修改过赋0
				}
			}
			if (d[i][j - 1] + 1< d[i - 1][j] + 1&& d[i][j - 1] + 1< d[i - 1][j - 1] + diff(s1[i - 1], s2[j - 1]))
			{
				c[i][j] = 2;//源于左方,赋2,对s1添加yj
			}
			if (d[i - 1][j] + 1 < d[i][j - 1] + 1 && d[i - 1][j] + 1 < d[i - 1][j - 1] + diff(s1[i - 1], s2[j - 1]))
			{
				c[i][j] = 3;//源于上方,赋3,对s1删除xi
			}
		} 
	}
	int ans = d[m][n];
	//将局部变量c[][]的值赋给全局变量ccc[][]
	for (int i = 1; i <= m; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			ccc[i][j] = c[i][j];
		}
	}

	//释放new的内存空间
	for (int i = 0; i <= m; i++)
	{
		delete[] d[i];//得到初始值全==0的二维数组
	}
	delete[] d;

	return ans;

}

void EDPrint(int i,int j)
{
	if (i == 0 || j == 0)
	{
		return;
	}

	if (ccc[i][j] == 0)
	{
		EDPrint(i - 1, j - 1);
		cout << "(" << i << "," << j << ")";
	}
	if (ccc[i][j] == 1)
	{
		EDPrint(i - 1, j - 1);
		cout << "(" << i << "," << j << ")";
	}
	if (ccc[i][j] == 2)
	{
		EDPrint(i , j - 1);
		cout << "(" << i << "," << j << ")";
	}
	if (ccc[i][j] == 3)
	{
		EDPrint(i - 1, j );
		cout << "(" << i << "," << j << ")";
	}
	

}​

 

三.Bug解惑

bug1:动态二维数组未初始化