算法分析 | 分支限界法 | 01背包问题

红色代表错误或者特别注意

蓝色代表修复后的正确代码

黄色表示变量

---

一.问题分析

1.问题的性质

回溯法是对树的深度遍历,需要用到递归.

分支限界法是对树的广度遍历,需要用到<queue>数据结构.而且每个状态都是一个数据结构实体

状态应该表示如下几个属性:

int cp    //已放入物品总价值

int rp    //剩余物品的总价值

int rw   //剩余容量

int id    //物品序号,比如某结点id=0,拓展当前结点时就要检查物品0  放入/不放入.

int[] x   //当前解向量

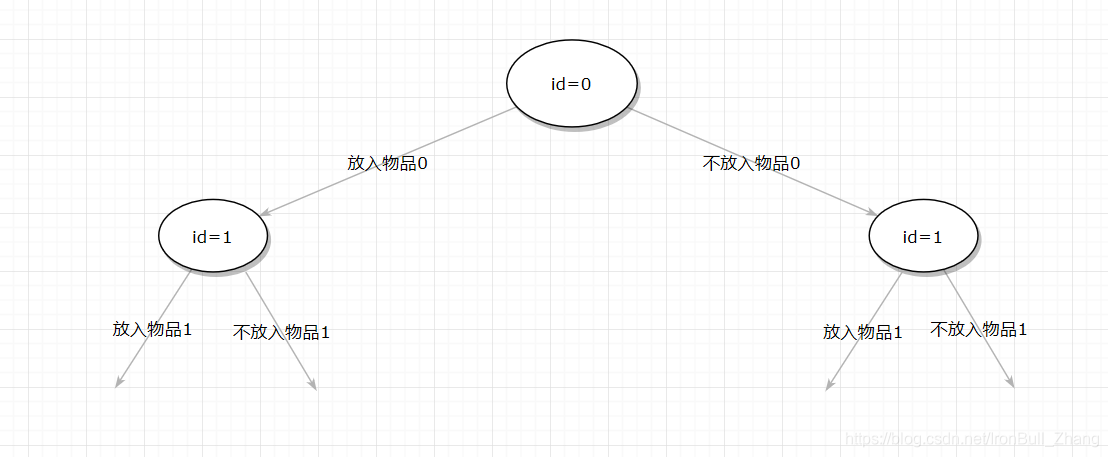
运算过程可以描述为:

将当前状态结点的符合条件的子结点push到队尾,并让当前节点出队.

2.限界条件&约束条件

01背包问题中,当前结点和左右子结点的限界条件和约束条件各不一样

当前结点:

      ①约束条件:什么情况下,当前结点无法生成左右子结点?

                        只有遍历完最后一个物品元素,或者容量=0时.看看此时能不能更新最优解. 最后当前结点出队并检查下一队列元素

      ②限界条件:什么情况下,当前结点没必要生成左右子节点?

                         当livenode.cp+livebode.rp<bestp时. 最后当前结点出队并检查下一队列元素

左子结点进行约束条件:当前剩余容量能够放入第t个物品

                          if(livenode.cp > W[ t ])      扩展lchild,lchild按条件赋值,id++

右子节点进行限界条件:不放入第t个物品,剩余价值--,计算已有价值和剩余价值是否大于最优解

                          if( livenode.cp + (livenode.rp - V[ t ]) ) > bestp

二.代码实现

分为三部分: 全局变量区  /  广度遍历函数  /  初始化&调用&显示函数

1.全局变量区

①一开始W[]和V[]在一个struct里,发现写出来有点繁琐:Good[i].value.

②每个结点都有cp来表示当前价值,不需要再像回溯法写在全局变量里

vector<int>W = { 2,5,4,2 };
vector<int>V = { 6,3,5,4 };
int N1 = (int)V.size();

int bestp1;						//记录最优值
vector<bool>bestx1;		//记录最优解

int Volume;							//记录购物车总容量
int sumv, sumw;			//全部物品总重量和总价值

//状态结构,记录下每个状态
struct State  
{
	int cp;						//当前状态的放入物品总价
	int rp;						//当前状态的剩余物品总价
	int rw;						//当前状态的剩余容量
	int id;						//物品号

	vector<bool> x;		//当前策略

	State()
	{
		cp = rp = rw = id = 0;
		x.resize(N1);
	}
	State(int _cp,int _rp,int _rw, int _id)		//构造函数,方便赋值,不必再写好几行赋值语句
	{
		cp = _cp;
		rp = _rp;
		rw = _rw;
		id = _id;
		x.resize(N1);
	}
};

 

2.广度遍历函数

int BFS_01Backpack()
{
	int t;//当前物品序号
	queue<State>q1;
	q1.push(State(0, sumv, Volume, 0));//已有物品总值,剩余物品总值,剩余容量,物品序号

	while (!q1.empty())		//开始循环
	{
		State livenode, lchild, rchild;		//每次循环创建当前结点,左子树,右子树
		livenode = q1.front();					//上一次while循环入队的左右孩子成为了新的livenode
		q1.pop();
		t = livenode.id;

		//终止条件
		if (t >= N1 || livenode.rw == 0)//物品序号 t=[0,N-1]	||	当前状态的剩余空间==0		
		{
			//多个可行解中得最优值
			if (livenode.cp >= bestp1)
			{
				bestx1 = livenode.x;
				bestp1 = livenode.cp;
			}
			continue;
		}

		//对活结点的限界条件
		if (livenode.cp + livenode.rp < bestp1)		
			continue;

		//左子树
		if (livenode.rw >= W[t])							//约束条件:剩余容量装得下当前物品
		{
							      //已有价值+,          剩余价值-,          剩余容量-,            序号比父结点+1
			lchild = State(livenode.cp + V[t], livenode.rp-V[t], livenode.rw - W[t], livenode.id + 1);
			lchild.x = livenode.x;
			lchild.x[t] =true;		//表示放入

			if (lchild.cp > bestp1)				//当前解>最优解才更新
				bestp1 = lchild.cp;

			q1.push(lchild);
		}
		
		//右子树
		if (livenode.cp + (livenode.rp - V[t]) >= bestp1)
		{
			                //已有价值不变,     剩余价值-,       剩余容量不变,   序号比父结点+1
			rchild = State(livenode.cp, livenode.rp-V[t], livenode.rw, t + 1);
			rchild.x = livenode.x;
			rchild.x[t] = false;
			q1.push(rchild);
		}
		
	}
	return bestp1;
}

 

3.初始化&调用&打印函数

void backpack()
{
	//初始化
	bestp1 = 0;
	Volume = 10;
	bestx1.resize(N1);
	sumw = accumulate(W.begin(), W.end(), 0);			//记录总重量
	sumv = accumulate(V.begin(), V.end(), 0);			//记录总价值
	

	//调用BFS()
	cout<<"最优值为:	"<<BFS_01Backpack();

	//输出
	cout << "放入的物品为:		";
	for (int i = 0; i < N1; i++)
	{
		if (bestx1[i] == true)
			cout << i << "	";
	}
	cout << endl;
	 
}

三.Bug分析

1.vector越界问题

忘记声明vector<bool> x时预设长度.

 

2.输出结果错误

右子树的约束条件出了问题,原错误代码:

    if (livenode.cp + livenode.rp >= bestp1)

右子树表示不放入物品t,剩余价值也一样要减少:

    if (livenode.cp + (livenode.rp - V[t]) >= bestp1)