密码学基础(八) - 数字签名
数字签名的相关定义
数字签名类似于私钥加密体系中消息认证码,不过数字签名不仅能够满足消息认证,而且能够满足身份认证以及抗抵赖性。
在发送方所使用的算法一般用Sign来表示,而这个算法的输出称为签名
在接收方输入一个消息以及一个签名进行验证的算法用Vrfy表示
数字签名的定义:一个数字签名算法由三个概率多项式的算法(Gen, Sign, Vrfy)组成:
- Gen:密钥生成算法,以一个安全参数1n作为输入,输出一对密钥(pk, sk),成为公钥以及私钥
- Sign:签名算法,以一个私钥sk以及一条明文作为输入,然后输出一个签名\(\sigma\),记作\(\sigma\leftarrow Sign_{sk}(m)\)
- Vrfy:验证算法,一个确定性函数,以一个公钥pk以及一个签名\(\sigma\)作为输入,如果\(Vrfy_{pk}(m,\sigma)=1\)则称\(\sigma\)是对于明文m的有效签名
显然对于明文空间中的每一条明文 m 都要能够满足\(Vrfy_{pk}(Sigh_{sk}(m))=1\)
如果存在一个函数l,使得由Gen生成的公私钥对应的明文空间为\(\lbrace 0,1\rbrace^{l(n)}\),则称(Gen, Sign, Vrfy)是对于消息长度为l的数字签名方案
数字签名的安全实验\(Sign-forge_{A,\Pi}(n)\):
- 运行Gen(\(1^n\))获得密钥(pk, sk)
- 敌手获取了公钥pk并且能够访问一个签名预言机Sigh(·),令集合Q表示敌手的所有查询。然后敌手伪造一个消息以及其对应的签名(m,\(\sigma\))。
- 如果(1)\(Vrfy_{pk}(m,\sigma)=1\),并且(2)\(m\notin Q\),则这个实验输出1,否则输出0
如果对所有PPT上的敌手A,存在一个可忽略函数negl使得,\(Pr[Sign-forge_{A,\Pi}(n)=1]\le negl(n)\),则称数字签名方案\(\Pi\)=(Gen, Sign, Vrfy)在自适应攻击下存在不可伪造性,或者称其为安全的
Hash-and-Sign
Hash-and-Sign范式:设\(\Pi\)=(Gen, Sign, Vrfy)是一个对于明文长度为l(n)的数字签名算法,并且\(\Pi_{H}\)=(\(Gen_H,H\))是一个输出长度为l(n)的哈希函数,则可以构造一个数字签名方案\(\Pi'\)为:
- Gen':输入一个安全参数\(1^n\),然后运行Gen(\(1^n\))获取密钥(pk, sk),然后运行\(Gen_H(1^n)\)获取s,则公钥为<pk, s>,私钥为<sk, s>
- Sign':输入一个私钥<sk, s>以及一条明文m \(\in\) {0, 1}*,输出\(\sigma\leftarrow Sign_{sk}(H^s(m))\)
- Vrfy':输入一个公钥<pk, s>,一条明文m \(\in\) {0, 1}*,以及一个签名\(\sigma\),如果\(Vrfy_{pk}(H^s(m), \sigma)=1\)则输出1,否则输出0
定理:如果\(\Pi\)是一个对于明文长度为l的安全的数字签名方案,并且\(\Pi_H\)是一个抗碰撞的哈希函数,则上面所构造的数字签名方案是安全的。
基于RSA加密方案的数字签名方案
首先讨论最简单的RSA加密方案,虽然这个方案是不安全的,但是却能很好的切入问题
普通的RSA加密方案
设GenRSA是一个PPT上的算法,输入一个安全参数\(1^n\),然后输出一个由两个n比特长的素数相乘得到的模数N,以及满足ed = 1 mod \(\varphi\)(N)的e和d
则可以构造一个基于普通RSA加密方案的数字签名方案:
- Gen:输入安全参数\(1^n\)并运行GenRSA(\(1^n\)),获得(N, e, d),则公钥为<N,e>,私钥为<N,d>
- Sigh:输入私钥sk = <N,d>以及一个明文m \(\in Z^*_N\),然后计算签名\(\sigma\) := \(m^d\) mod N
- Vrfy:输入公钥pk = <N,e>,一个明文m \(\in Z^*_N\),以及一个签名\(\sigma \in Z^*_N\),如果 m = \(\sigma^e\) mod N,则输出1,否则输出0
普通RSA数字签名方案的不安全性:
- RSA困难问题假设只是针对于随机的消息m而言的,但是却没有保证对于某个确定的或者由敌手选择的消息的困难性
- 此外,RSA困难问题假设对于敌手在了解了其他消息的签名后可能会做些什么没有任何说明
- 无消息伪造:给定公钥<N,e>,随机的选择一个签名\(\sigma \in Z^*_N\),然后计算m := \(\sigma^e\) mod N,则显然(m, \(\sigma\))是一对有效的伪造
- 利用普通RSA加密方案的同态性可以伪造任意长度消息的签名
RSA-FDH以及PKCS#1 V2.1
上面所提及的攻击方案,其实可以通过先对明文进行一些转换来避免
而RSA-FDH就是利用一个具备某些特定的密码学属性的函数从而进行签名的
the RSA full-domain hash (RSA-FDH)数字签名方案:设存在一个GenRSA,则可以构造一个数字签名方案如下:
- Gen:运行GenRSA(\(1^n\))来获取(N,e,d),公钥为<N,e>,私钥为<N,d>。此外,函数H:{0,1}* \(\to Z^*_N\)也作为密钥生成算法的一部分
- Sign:输入一个私钥<N,d>以及一个消息m \(\in\) {0,1}*,计算\(\sigma := H(m)^d\) mod N
- Vrfy:输入一个公钥<N,e>,一个消息m,以及一个签名\(\sigma\),如果\(\sigma^e = H(m)\) mod N,则输出1,否则输出0
该方案中的函数H应该具备的属性:
- 为了抵抗无消息攻击,H应该很难求逆
- 为了抵抗利用同态性的消息伪造,H应该不具备乘法同态性,即不存在三条消息\(m,m_1,m_2\)满足\(H(m)=H(m_1)·H(m_2)\) mod N
- 为了数字签名的功能性,H应该很难找到碰撞,否则如果H(\(m_1\))=H(\(m_2\)),那么\(m_1\)和\(m_2\)就有了相同的签名
显然,随机预言机是满足上面的性质的
定理:如果RSA问题相对于GenRSA来说是困难的,而H是一个随机预言机,则上面所构造的数字签名方案是安全的
基于离散对数问题的数字签名方案
同样的,也可以基于离散对数的困难问题假设来设计数字签名方案
Fiat-Shamir转换
识别方案
这里首先介绍一下识别方案(Identification Scheme),所谓识别方案其实就是一个互动式协议,用于通信方向对方证明其身份
这实际上是个非常常见的概念,比如在登陆某个网站时需要向服务器识别(或者说是认证)自己的身份,识别协议成功执行了后将会使验证方相信当前是在和真正的认证者进行交流。
识别方案属于一种零知识证明,也就是向对方证明知道某个秘密,但是又不透露这个秘密的信息。
这里主要关注一种公钥下的识别协议,也就是证明者(Prover)和验证者(Verifier)并不会事先共享某个秘密来完成识别,相反,验证者只知道证明者的公钥。
下图是一个三轮的识别协议,其中证明者用两个算法\(\mathcal{P}_1, \mathcal{P}_2\)标识,验证者用算法\(\mathcal{V}\)标识:
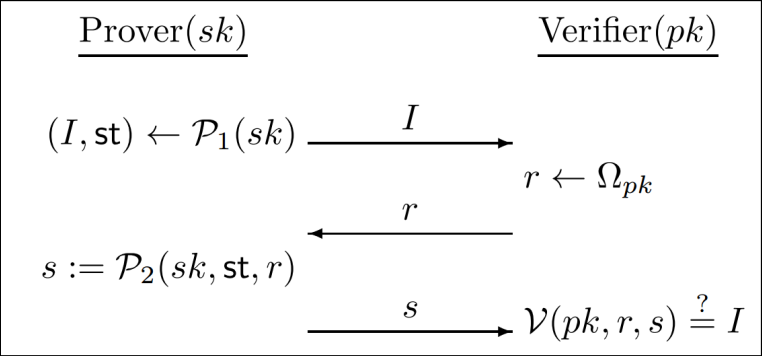
算法流程如下:
- 证明者使用自己的私钥运行算法\(\mathcal{P}_{1}(sk)\)以生成初始消息\(I\),以及状态信息\(st\),然后将初始消息\(I\)发送给验证者
- 验证者收到初始消息\(I\)后,从挑战集合(set of chanllengs),\(\Omega_{pk}\),中概率均匀的选择一个挑战\(r\)作为响应,其中\(\Omega_{pk}\)由证明者的公钥定义
- 证明者运行算法\(\mathcal{P}_2(sk, st, r)\)生成\(s\),并发送给验证者,验证者随即运行算法\(\mathcal{V}(pk, r, s)\)验证算法结果是否等于初始消息\(I\)
出于技术原因,一般认为认证协议是非退化(non-degenerate)的,也就是说对于任意私钥\(sk\)以及一条固定的初始消息\(I\),\(\mathcal{P}_1(sk)\)输出I的概率是可忽略的。
认证方案的基本安全需求就是对于任何一个不知道密钥的敌手,成功欺骗验证方的概率是可忽略的,这个安全条件需要保证即使在敌手能够被动的在验证方和认证放通信过程中进行窃听也成立。
为了模拟敌手的窃听能力,给定敌手一个预言机,不需要任何输入而直接返回识别过程中的\((I,r,s)\)
设\(\Pi=(Gen,\mathcal{P}_1,\mathcal{P}_2,V)\)是一个识别协议,则其安全实验为
认证方案的安全实验\(Ident_{A,\Pi}(n)\):
- 运行\(Gen(1^n)\)获取密钥\((pk, sk)\)
- 敌手已知公钥\(pk\),并且可以访问预言机\(Trans_sk(\cdot)\)
- 在实验中的任何时刻,敌手输出一个初始明文\(I\),则验证方概率均匀的选择一个\(r \in\Omega_{pk}\)返回给敌手A,然后A在返回一个s(敌手即使在收到了r后依然可以访问预言机)
- 如果\(V(pk, r, s) = I\),则输出1;否则,输出0
如果对所有PPT上的敌手\(\mathcal{A}\),存在一个可忽略函数negl满足Pr[\(Ident_{\mathcal{A},\Pi}(n)=1\)] \(\le\) negl(n),则称认证方案\(\Pi=(Gen,\mathcal{P}_1,\mathcal{P}_2,\mathcal{V})\)是抵抗被动攻击的,或者称其是安全的。
基于认证方案构造数字签名方案
Fiat-Shamir转换,提供一种将任意(交互式)识别方案转换成(非交互式)数字签名方案。其基本思想是,让签名方以证明者的身份运行识别方案 (by itself),其具体构造方法如下:
设\((Gen_{id},\mathcal{P}_1,\mathcal{P}_2,\mathcal{V})\)是一个认证方案,则可以构造一个数字签名方案如下:
- Gen:输入一个安全参数\(1^n\),然后运行\(Gen_{id}(1^n)\)获取密钥\((pk,sk)\),其中公钥\(pk\)确定了一个挑战集合\(\Omega_{pk}\),此外还有一个函数\(H:\{0,1\}*\to\Omega_{pk}\),将任意输出映射到挑战集合中
- Sign:输入一个私钥\(sk\)以及一条明文\(m \in \{0,1\}*\):
- 计算\((I,st)\leftarrow \mathcal{P}_1(sk)\)
- 计算\(r := H(I,m)\)
- 计算\(s := \mathcal{P}_2(sk,st,r)\)
输出签名\((r,s)\)
- Vrfy:输入一个公钥\(pk\),一个明文\(m\),以及一个签名(r,s),计算\(I' := V(pk, r, s)\),如果\(H(I',m)=r\)则输出1,否则输出0
定理:设\(\Pi\)是一个认证方案,\(\Pi'\)是一个由Fiat-Shamir转换构造的数字签名方案,如果\(\Pi\)是安全的,并且\(H\)是一个随机预言机,则\(\Pi'\)也是安全的
Schnorr数字签名
这里介绍一个实例,通过Schnorr识别方案,构造出Schnorr数字签名方案。
Schnorr认证方案的运行原理是基于离散对数问题的,公钥\((\mathrm{G}, q, g, y)\),私钥\(x\),其中\(y=g^x\mod q\):
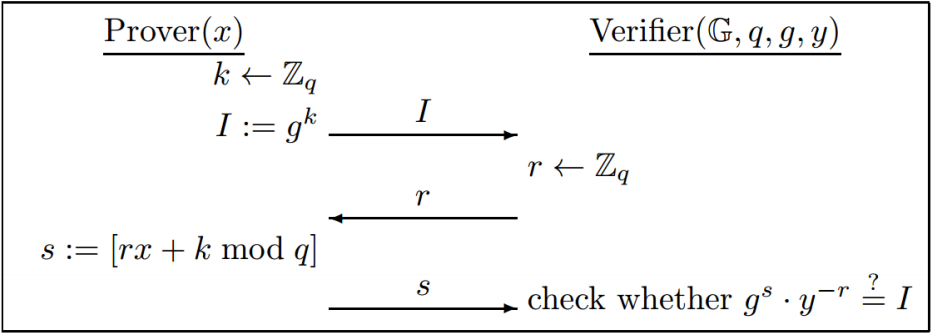
如果离散对数问题对于G是困难的,则Schnorr识别方案是安全的
通过Fiat-Shamir转换,可以构造Schnorr数字签名方案:
- Gen:运行\(G(1^n)\)获取\((G,q,g)\),概率均匀的选择一个\(x \in Z_q\),令\(y := g^x\),则私钥为\(x\),公钥为\((G,q,g,y)\),函数\(H:{0,1}* \to Z_q\)也作为密钥生成算法的一部分
- Sign:输入一个私钥\(x\),以及一条明文\(m \in {0,1}*\),概率均匀的选择一个\(k \in Z_q\),令\(I := g^k\),然后计算\(r:=H(I,m), s:=rx+k \mod q\),输出签名\((r,s)\)
- Vrfy:输入一个公钥\((G,q,g,y)\),一条明文\(m\),以及一个签名\((r,s)\),计算\(I:=g^s·y^{-r}\),如果\(H(I,m)=r\)则输出1,否则输出0
DSA以及ECDSA
数字签名算法(Digital Signature Algorithm, DSA)和椭圆曲线数字签名算法(Elliptic Curve Digital Signature Algorithm, ECDSA)是两个在不同类型的群的离散对数问题设计的数字签名方案
这两种方案都遵循一个公共模板,可以看作是由底层认证方案构造的。
设G是一个素阶循环群,生成因子为g,则有一个认证方案,其认证方的私钥为x,公钥为(G,q,g,y),其中\(y=g^x\)
- 认证方概率均匀的选择一个k \(\in Z^*_q\),然后令I:=\(g^k\)
- 验证方随机的选择并发送一个\(\alpha,r\in Z_q\)作为挑战
- 认证方发送一个s:=\(k^{-1}(\alpha+xr)\) mod q作为回应
- 如果s \(\ne\) 0,并且\(g^{\alpha s^{-1}}·y^{rs^{-1}}=I\),则接收验证
如果\(\alpha=-xr\) mod q,则s=0,而这种情况发生的概率是可忽略的
当s \(\ne\) 0时,则\(s^{-1}\)是存在的,该认证方案的正确性:
\(g^{\alpha s^{-1}}·g^{rs^{-1}}=g^{\alpha s^{-1}}·g^{xrs^{-1}}=g^{s^{-1}(\alpha+xr)}=g^{k(\alpha+xr)^{-1}(\alpha+xr)}=g^k=I\)
DSA\ECDSA数字签名方案是通过签名者将上面的认证方案"压缩"进一个非交互式的算法中的实现的
DSA:
- Gen:输入安全参数\(1^n\),运行G(\(1^n\))获取(G,q,g),概率均匀的选择一个x \(\in Z_q\)然后令y:=\(g^x\),则公钥为(G,q,g,y),而私钥为x
此外,作为密钥生成算法中的一部分,还有两个函数H:{0,1}* \(\to Z_q\)以及H:F \(\to Z_q\) - Sign:输入私钥x以及一条明文m \(\in\) {0,1}*,概率均匀的选择一个k \(\in Z^*_q\),然后令r := F(\(g^k\)),计算s := \(k^{-1}(H(m)+xr)\) mod q,(如果r或s等于0则重新启动算法),输出签名(r,s)
- Vrfy:输入公钥(G,q,g,y),一条明文m \(\in\) {0,1}*,以及一个签名(r,s),如果r = F(\(g^{H(m)·s^{-1}}·g^{r·s^{-1}}\)),则输出1,否则输出0
如果离散对数问题是困难的,并且H和F是随机预言机,那么可以证明DSA和ECDSA是安全的
k的合适选择:如果k选择不当,则会导致灾难性的后果
- 对于初学者,如果敌手能够预测出对于消息m的数字签名(r,s)中使用k,则可以计算出签名者的私钥,因为s=\(k^{-1}\)·(H(m)+xr) mod q
- 即使k是难以预测的,如果使用同一个k来对两个不同的明文进行签名,则敌手仍然能够计算出签名者的私钥
设(r,\(s_1\)),(r,\(s_2\))是对于明文\(m_1\),\(m_2\)的签名,
\(s_1=k^{-1}·(H(m_1)+xr)\) mod q
\(s_2=k^{-1}·(H(m_2)+xr)\) mod q
\(s_1-s_2=k^{-1}(H(m_1)-H(m_2))\) mod q,从而能够计算出k,有了k,也就可以计算出签名者的私钥

 浙公网安备 33010602011771号
浙公网安备 33010602011771号