4、步进电机S形加减速
1、 S 形加减速原理分析
S 形加减速可以理解为在加减速的变化过程中速度曲线呈现一个英文字母“S”形的加减速算法。那么已经有了梯形加减速算法了,为什么还需要 S 形加减速算法呢?答案很明显,由于不同的加减速算法的特点是不一样的,所以带来的效果自然而然的就不同了。
梯形加减速在启动、停止和高速运动的过程中会产生很大的冲击力振动和噪声,所以多数会应用于简单的定长送料的应用场合中,例如常见的 3D 打印机使用的就是梯形加减速算法;但是相比较 S 形加减速在启动停止以及高速运动时的速度变化的比较慢,导致冲击力噪音就很小,但这也决定了他在启动停止时需要较长的时间,所以多数适用于精密的。
1.1、 “S”模型解析
S 形加减速算法对于曲线并没有具体的限定和轨迹,可以是指数函数、正弦函数只要满足于速度的变化曲线是一个“S”形即可;
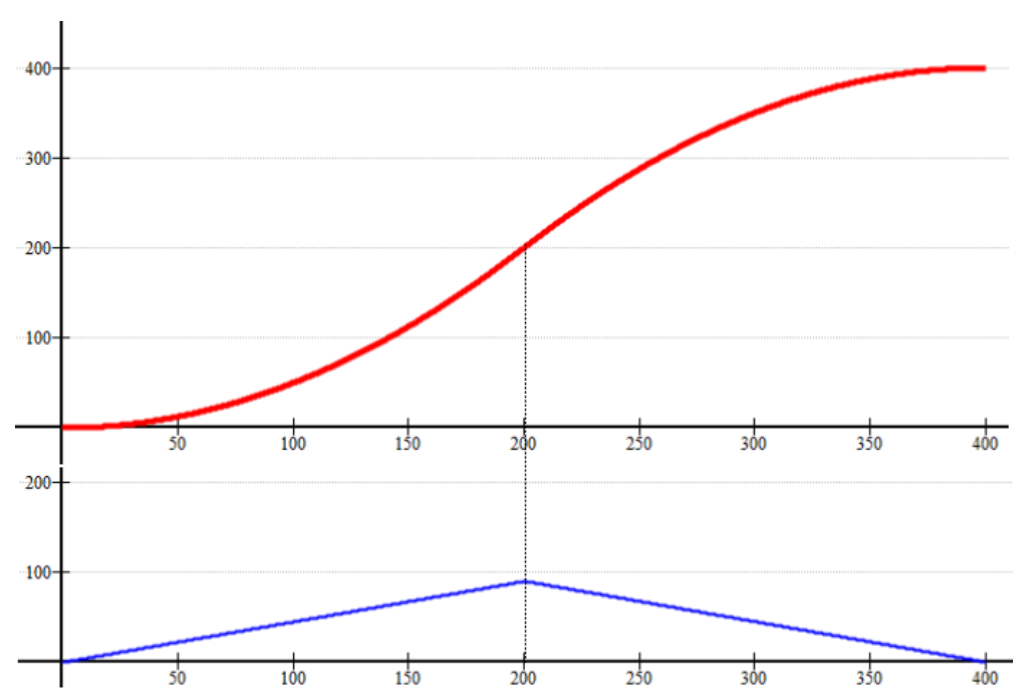
具体的曲线情况如上图。在上图中一共有两幅曲线图像,其中红色的是速度的曲线,可以看出整体都属于速度的上升阶段,在加速的过程中一共可以分为两个阶段,分别为前半部分和后半部分,前半部分是加速度匀速递增的曲线,称为: 加加速阶段曲线,后半部分是加速度匀速递减的曲线超,所以称为: 减加速度阶段曲线。
上图中蓝色的曲线是加速度的变化曲线,按照速度变化的规律共分成前半段加速度匀速递增和后半部分加速度匀速递减,也可以简单理解为一次函数,前半段一次函数的斜率是大于 0 的,后半部分的斜率是小于 0 的;加速度从 0 开始变化,到了最大值开始减小,最后为 0,由于加速度的斜率是相同的,所以斜率大于 0 和小于 0 两段曲线是关于加速度最大值所对应的速度中心对称的。
1.2 、算法理论实现
下图共有三条曲线分别是红色、青色和蓝色,其中红色速度曲线、蓝色加速度曲线,青色为梯形加减速模型的加速部分的速度曲线。
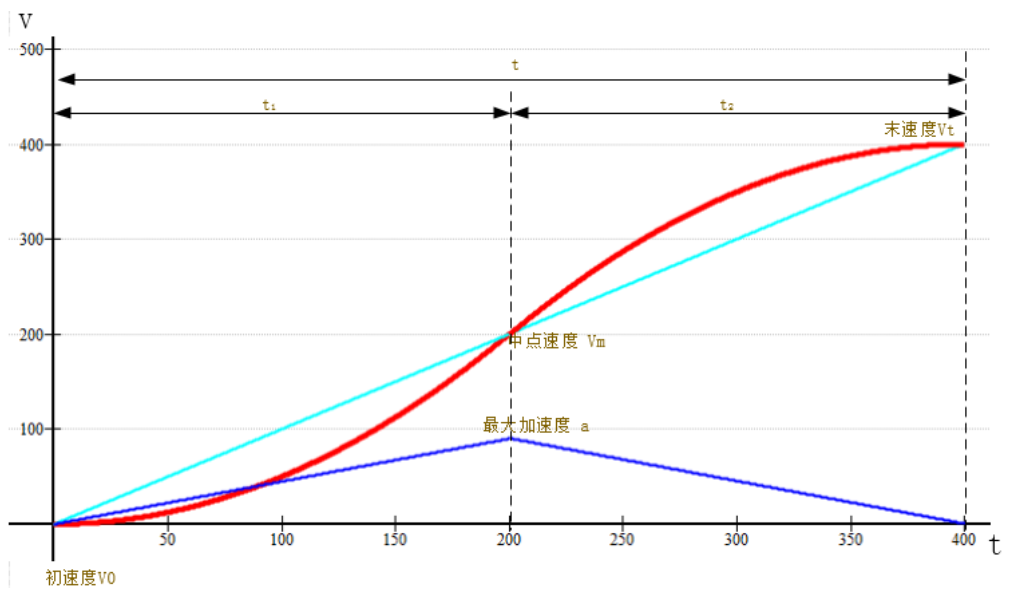
图中是梯形加速度部分(青色曲线)和 S 形加速部分(红色曲线)比较,梯形加减速是按照一个固定的斜率增加速度到达 Vt, 到达 Vt 后加速部分结束,开始进入匀速部分,梯形加减速由匀加速上升的趋势突然变成匀速,由于惯性会产生较大的冲击力和噪声; S 形加减速则很好的避免了这一问题,在加速到 Vt 后进入匀速阶段曲线上非常的顺滑,阶段衔接的相对完美。
主要的目的是通过初速度、末速度和时间三个变量计算出控制步进电机的每一步速度;
(1)基础公式推导
加速度 a 从 0 变化到最大值有:
//公式1
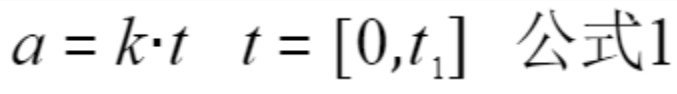
a表示加速度:
k为一次函数斜率,即加速度的斜率
t为时间变化
加速度也是按斜率k随时间t匀速变化的
//公式2
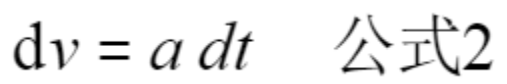
这是微分形式的速度与加速度关系。
物理意义:
dv:速度的微小变化量
a:瞬时加速度
dt:时间的微小变化量
在极短的时间 dt 内,速度的变化量 dv 等于加速度 a 乘以时间间隔 dt。
为什么成立:
从加速度的定义:
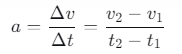
当时间间隔无限小(Δt→0)时,写成微分形式:
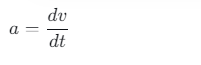
两边乘以 dt 就得到:
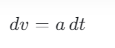
对加速度积分就可以得到速度,所以有:
//公式3
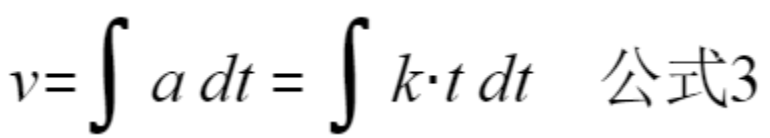
这是积分形式,从加速度求速度。
物理意义:
v:速度(是加速度对时间的积分)
∫adt:加速度对时间积分
特别地,当
a=k⋅t 时,代入得到
∫ktdt
根据公式三可得:
//公式4
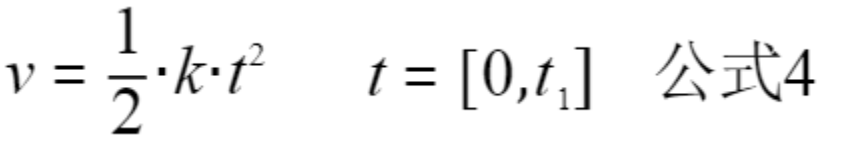
推导过程:

其中 C=C2−C1 是积分常数,由初始条件确定。
如上图所示:当 加速度 a 随着时间变化到最大值时速度 V=Vm, 并且初速度 V0=0,将这两个条件带入公式 4,可求得 斜率 k:
//公式5
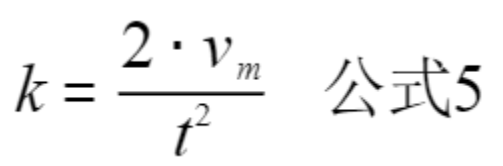
对速度积分就可以得到位移,所以有:
//公式6
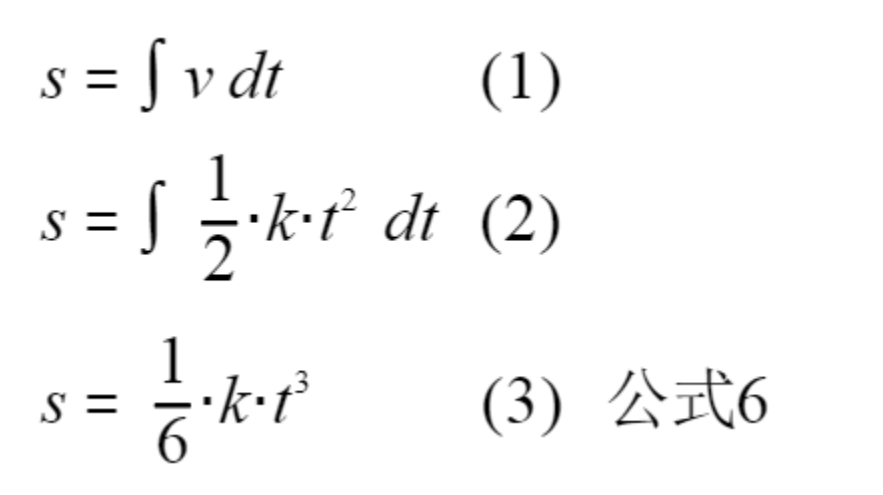
其中:
1. 对速度进行积分;
2. 将 速度 v 的表达式带入;
3. 求解速度积分的计算结果,并得到位移与时间的公式,即 公式 6;

根据 公式6可以很清楚的看到只要给定一个合适的 t 值,比如 1 秒内加速 1000 次,也就是t1=1/1000 那就可以得到一个比较平滑的速度曲线。
(2)速度推导
步进电机的速度是由定时器脉冲的频率决定的,频率越快也就是步进电机的速度越快,所以可以得出 脉冲输出的频率 = 速度,所以有:
//公式7

所以说只要计算出第一步的周期时间就可以计算出下一步的速度;并且根据时间的变化每计算一次就会累加一次时间变化量 Sumt。
在上图中:
• T 代表但脉冲周期
• f 代表频率
• speed 代表速度
每一步的速度都是在初始速度的基础上计算的,所以说 公式 4 计算的是当 初始速度为 0 时的增量,具体公式如下:
//公式8
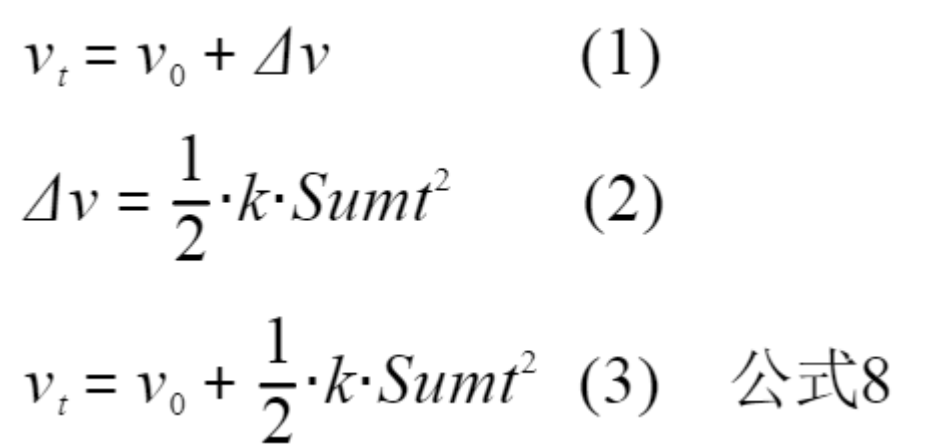
1. t 时刻的速度等于初始速度与增量速度的和;
2. 求解增量速度,并且将累计时间变量带入 公式 4;
3. 带入求解 t 时刻的速度;




 浙公网安备 33010602011771号
浙公网安备 33010602011771号