PID调试方法

1、采样周期选择

　　采样数据控制系统中，设采样周期为Ts，采样速率为1/Ts，采样角频率为w=2π/Ts，采样周期Ts是设计者精心选择的重要参数，系统的性能与采样周期的选择有密切关系。采样周期指的是 PID 控制中实际值的采样时间间隔，其越短，效果越趋于连续，对于大多数算法缩短采样周期可使控制回路性能改善，但对硬件资源的占用也越高，对有些变化缓慢的受控对象无需很高的采样频率即可满意地进行跟踪，过多的采样反而没有多少实际意义。

　　根据采样定律可以确定采样周期的上限值。实际采样周期的选择还要受到多方面因素的影响，不同的系统采样周期应根据具体情况来选择。
　　采样周期的选择，通常按照过程特性与干扰大小适当来选取采样周期：即对于响应快波动大、易受干扰(如流量、压力)的过程，应选取较短的采样周期，反之，当过程响应慢、滞后大(如温度、成份)时，可选取较长的采样周期。
　　采样周期的选取应与PID参数的整定进行综合考虑，采样周期应远小于过程的扰动信号的周期，在执行器的响应速度比较慢时，过小的采样周期将失去意义，因此可适当选大一点;在计算机运算速度允许的条件下，采样周期短，则控制品质好;当过程的纯滞后时间较长时，一般选取采样周期为纯滞后时间的1/4~1/8。

　　 在实际的应用中，我们可以使用理论或者经验方法来确定采样周期：
　　① 理论方法：香农采样定理。这个定理可以用来确定采样周期可选择的最大值，当采样周期超出了这个最大的允许范围，我们所得到的信号就会失真，也就无法较好地还原信号了。为不失真地复现信号的变化，采样频率至少应大于或等于连续信号最高频率分量的二倍。
　　② 经验方法：根据控制对象突变能力选择。假设电机当前转速为 20RPM，我们需要提高它的转速到 30RPM，此电机的转速在 1s 之内最大可以突变 10RPM（即电机速度的突变能力），如果我们每 1ms 采集一次电机转速，那么每一次采集到的速度变化量最大为 10RPM / 1000 =0.01RPM，很明显，此时最大的变化量远远小于当前的速度，这对于我们的 PID 控制效果并没有明显的提升，但是却占用了很多的硬件资源，因此，我们需要根据控制对象的突变能力来选择采样周期。

2、PID 参数整定方法

　　控制器参数整定：指决定调节器的比例系数Kp、积分时间Ti、微分时间Td和采样周期Ts的具体数值。
　　整定的实质是通过改变调节器的参数，使其特性和过程特性相匹配，以改善系统的动态和静态指标，取得最佳的控制效果。

　　PID 参数整定的方法很多，概括起来有两大类，如下表所示：

 　　　　　　　　　　　　　　　　PID 参数整定方法

　　理论计算整定法： 理论计算整定法有对数频率特性法和根轨迹法等。依据系统的数学模型，经过理论计算确定 PID 参数。这种方法是建立在理想化条件下的，其得到的参数不一定能够直接使用， 还需要结合经验以及实际的系统进行调整。
　　工程整定法：工程整定法特点不需要事先知道过程的数学模型，依靠工程经验，直接在过程控制系统中进行现场整定，方法简单、计算简便、易于掌握，在实际调参中被广泛采用。工程整定法包括凑试法、临界比例法、经验法、衰减曲线法和响应曲线法等。

　　PID调节系统在设计、整定和运行中，衡量系统质量的依据就是系统的过渡过程。当系统的输入为阶跃变化时，系统的过渡过程大多表现形式为振荡过程，如发散振荡、等幅振荡、衰减振荡、单调过程等形式。但在大多数情况下，都希望得到衰减振荡这种过渡过程，因此它是用来衡量控制系统质量的依据。

　　发散震荡：离目标值越来越远。
　　等幅震荡：类似于正弦波，偏差保持不变。
　　衰减震荡：离目标值越来越近。
　　单调过程：响应比较缓慢。

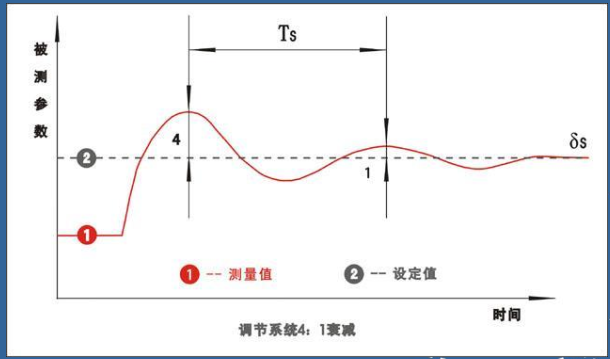
　　调节系统4:1衰减：即两个波峰离目标值的差为4:1时，这种为衰减震荡中最好的一种，即两个波峰后就差不多到目标值了。

　　注意： 无论采用哪一种方法所得到的 PID 参数，都需要在实际运行中进行最后调整与完善，因此，在 PID 参数整定中，最重要的就是经验的积累。

　　接下来我们了解一下 PID 各个系数调节的效果，这样才能做到在 PID 调参中有的放矢。
　　① 比例系数：调节作用快，系统一出现偏差，调节器立即将偏差放大输出。
　　② 积分系数： 积分系数的调节会改变输入偏差对于系统输出的影响程度。积分系数越大，消除静差的时间越短，但是过大的积分系数则会导致系统出现超调现象，这在具有惯性的系统中尤为明显。
　　③ 微分系数：微分系数的调节是偏差变化量对于系统输出的影响程度。微分系数越大，系统对于偏差量的变化越敏感，越能提前响应，进而抑制超调，但是过大的微分系数则会让整个系统出现振荡。
　　（1）试凑法

　　采样周期的选择，要根据所设计的系统的具体情况，用试凑的方法，在试凑过程中根据各种合理的建议来预选采样周期，多次试凑，选择性能较好的一个作为最后的采样周期。早整定参数时必须要认真的观察系统的相应情况，根据系统的响应情况来调整参数。在调节参数时应该知道各种参数调节的特点，才能有的放矢；
　　• 比例调节作用特点：调节作用快，系统一出现偏差，调节器立即将偏差放大输出；
　　• 积分调节作用特点：积分调节作用的输出变化与输入偏差的积分成正比，积分调节作用的输出不仅取决于偏差的大小，还取决于偏差存在的时间，只要有偏差存在, 尽管偏差可能很小，但它存在的时间越长，输出信号就越大，只有消除偏差，输出才停止变化；
　　• 微分调节作用特点：微分调节的输出是与被调量的变化率成正比，微分调节越大，越能提前响应，但是也会将不必要的偏差放大；

　　1）内容：结合系统的具体情况以及经验，先试凑几组合理的 PID 系数，同时需要观察系统的曲线变化，确定每一个系数对于整个系统曲线的大致影响，然后再根据具体的曲线进行调整。
　　2）调节思路：
　　① 先是比例（P），再积分（I），最后是微分（D），调试时，将 PID 参数置于影响最小的位置，即 P 最大， I 最大， D 最小；
　　② 按纯比例系统整定比例系数，使其得到比较理想的调节过程曲线，然后再把比例系数缩小 1.2 倍左右，将积分系数从小到大改变，使其得到较好的调节过程曲线；
　　③ 在这个积分系数下重新改变比例系数，再看调节过程曲线有无改善；
　　④ 如有改善，可将原整定的比例系数减少，改变积分系数，这样多次的反复，就可得到合适的比例系数和积分系数；
　　⑤ 如果存在外界的干扰， 系统的稳定性不好， 可把比例、积分系数适当减小， 使系统足够稳定；
　　⑥ 如果系统存在小幅度超调， 可以将整定好的比例系数和积分系数适当减小， 增大微分系数，以得到超调量最小、调节作用时间最短的系统曲线；

　　按照先比例(P)、再积分 (1)、最后微分 (D)的顺序。
　　①置调节器积分时间Ti=∞(Ki=Kp/Ti，所以Ki=0)，微分时间Td=0 (Kd=Kp*Td，所以kd=0) ，在比例系数Kp按经验设置的初值条件下，将系统投入运行，由小到大整定比例系数。求得满意的 4:1 衰减度过渡过程曲线。

　　②引入积分作用(此时应将上述比例系数Kp设置为5/6 Kp) 。将Ti由大到小进行整定。
　　③若需引入微分作用时，则将Td按经验值或按Td=(1/3~1/4) Ti设置，并由小到大加入。

　　（2）临界比例法

　　临界比例法：适用于闭环控制系统里将调节器置于纯比例的作用下，从大到小逐渐改变调节器的比例度，并且得到等幅度的震荡过程就叫做临界比例度；
　　1）内容： 在闭环的控制系统里，将调节器置于纯比例作用下，从小到大逐渐调节比例系数， 直到系统曲线出现等幅振荡，再根据经验公式计算参数。
　　2）调节思路：
　　① 将积分、 微分系数置零，比例度取适当值，平衡操作一段时间， 使控制系统按纯比例作用的方式投入运行。
　　② 慢慢地增大比例系数，细心观察曲线的变化情况。如果控制过程的曲线波动是衰减的，则把比例系数继续增大；如果曲线波动是发散的，则应把比例系数减小，直至曲线波动呈等幅振荡， 此时记下临界比例系数 δK 和临界振荡周期 Tk 的值。
　　③ 根据记下的比例系数和周期，采用经验公式，计算调节器的参数。

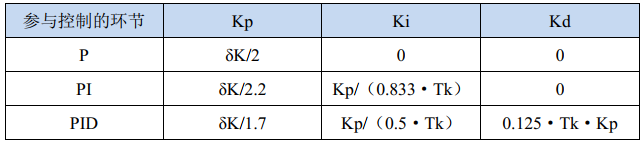
　　在闭环控制系统里，将调节器置于纯比例作用下，从小到大逐渐改变调节器的比例系数，得到等幅振荡的过渡过程，此时的比例系数称为临界比例系数Ku，相邻两个波峰间的时间间隔，称为临界振荡周期Tu。
　　临界比例度法步骤：
　　①将调节器的积分时间Ti置于最大(Ti =∞)，Ki为0，微分时间置零(Td =0),Kd为0 ，比例系数kp适当，平衡操作一段时间，把系统投入自动运行。
　　②将比例系数Kp逐渐增大，得到等幅振荡过程，记下临界比例系数Ku和临界振荡周期Tu值。
　　③根据Ku（等幅振荡时的比例系数）和Tu（相邻两个波峰的时间间隔）值，采用经验公式，计算出调节器各个参数，即Kp、Ti和Td的值。
　　④按“先P再I最后D”的操作程序将调节器整定参数调到计算值上。若还不够满意，可再作进一步调整。

　　这种临界比例法只针对模拟PID控制器，对于数字PID控制器，只要采样周期取的较小，原则上也同样使用。在电动机的控制中，可以先采用临界比例法，然后在采用临界比例法求得结果的基础上，用凑试法进一步完善。

　　（3）经验法

　　用凑试法确定PID参数需要经过多次反复的实验，为了减少凑试次数，提高工作效率，可以借鉴他人的经验，并根据一定的要求，事先作少量的实验，以得到若于基准参数，然后按照经验公式，用这些基准参数导出PID控制参数，这就是经验法。
　　临界比例法就是一种经验法。这种方法首先将控制器选为纯比例控制器，并形成闭环改变比例系数，使系统对阶跃输入的响应达到临界状态，这时记下比例系数Ku、临界振荡周期为Tu，根据Z一N提供的经验公式，就可以由这两个基准参数得到不同类型控制器的参数。

　　Ziegler-Nichols 方法分为两步：
　　①构建闭环控制回路，确定稳定极限。
　　②根据公式计算控制器参数。
　　稳定极限是由 P 元件决定的。当出现稳态振荡时就达到了这个极限。产生了临界系数 Kpcrit 和临界振荡周期 Tcrit。

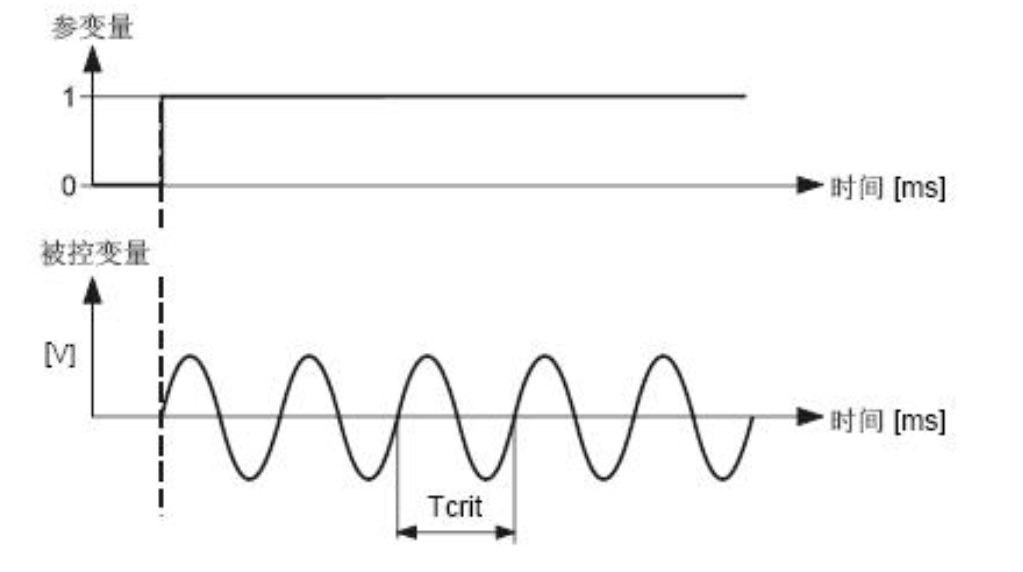
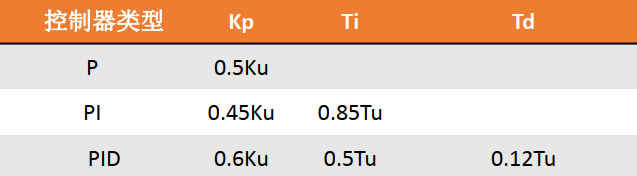
 　　确定临界系数 Kpcrit 和临界振荡周期 Tcrit 后，根据下表的公式，计算其他参数：

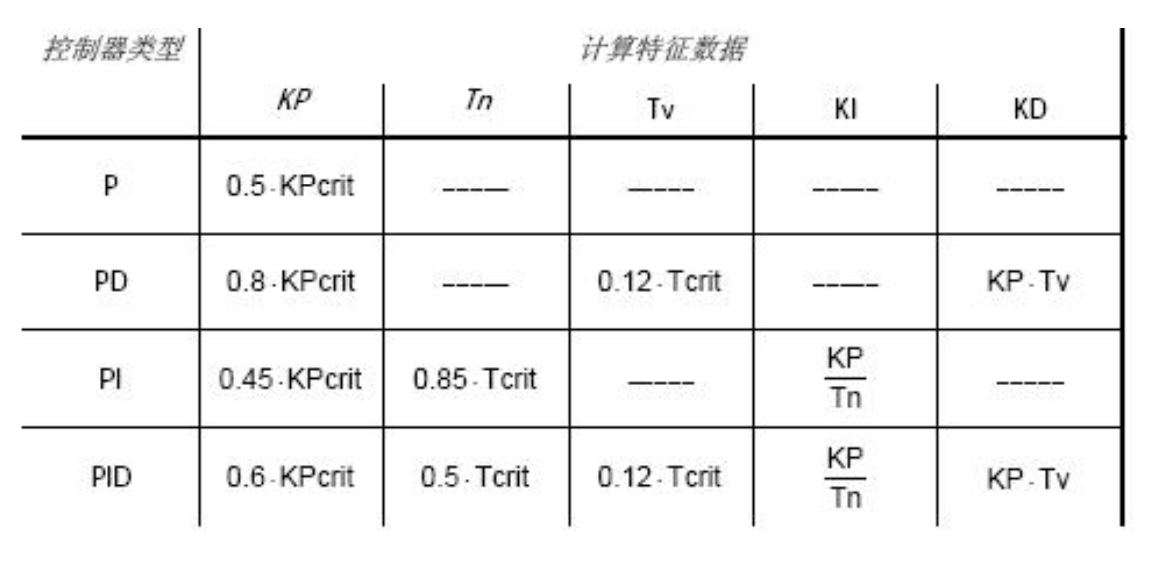
　　根据上述方法，举例说明：假设 Kpcrit=20，Tcrit=100ms
　　确定 PID 控制器的 P、I、D 元件的系数以及积分时间内 Tn 和微分时间 Tv。
　　优化 PID 控制器的参数：

　　综上可以看出，在调试 PID 控制器时，如果应用 Ziegler-Nichols 方法，可以快速、精确的算出相应的各参数数值，再之后只需进行微调便可得到理想的控制效果。

 

　　（4）一般调节法
　　1）内容：这种方法针对一般的 PID 控制系统所以称之为一般调节法。其中 Kp 是加快系统响应速度，提高系统的调节精度； Ki 用于消除稳态误差； Kd 改善系统的稳态性能。

　　a. 在输出不振荡时，增大比例增益 P。
　　b. 在输出不振荡时，减小积分时间常数 Ti。
　　c. 在输出不振荡时，增大微分时间常数 Td。
　　（它们三个任何谁过大都会造成系统的震荡。）

　　2）调节思路：
　　① 首先将积分、微分系数置零， 使系统为纯比例控制。 控制对象的值设定为系统允许的最大值的 60%~70%， 接着逐渐增大比例系数，直至系统出现振荡；此时再逐渐减小比例系数，直至系统振荡消失， 然后记录此时的比例系数， 并设定系统的比例系数为当前值的 60%~70%。
　　② 确定比例系数后，设定一个较小的积分系数，然后逐渐增大积分系数，直至系统出现振荡；此时在逐渐减小积分系数， 直至系统振荡消失，然后记录此时的积分系数，并设定系统的积分系数为当前值的 55%~65%。
　　③ 微分系数一般不用设定，为 0 即可。若系统出现小幅度振荡， 并且通过 PI 环节无法优化，这可以采用与确定比例、积分系数相同的方法， 微分系数取系统不振荡时的 30%左右。
　　④ 系统空载、带载联调，再对 PID 参数进行微调，直至满足要求。

　　（5）实际调参演示
　　接下来我们将从实际的 PID 系统曲线来理解 PID 各个系数的调节效果，大家一定要注意经验的积累。我们调节 PID 系数的思路如下：
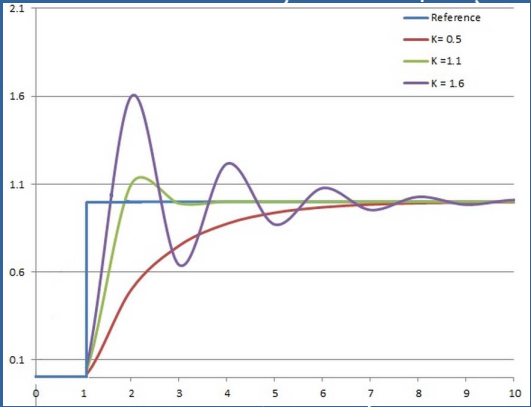
　　① 先调整比例系数，积分、 微分系数设置为 0，此时的系统只有比例环节参与控制。如果此时系统的曲线出现大幅振荡，如下图所示：

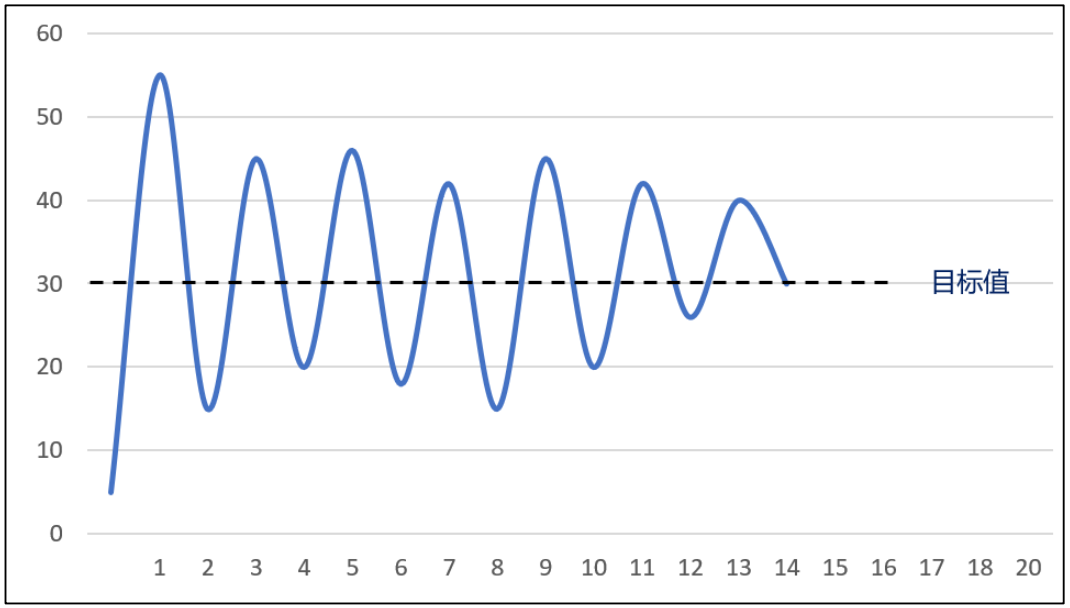
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　PID 曲线出现大幅振荡

　　首先确定硬件上是否出现了故障，例如电压不稳定、电机堵转等，排除了这些之后，那就说明比例系数调节的过大了，这个时候我们可以把比例系数慢慢地减小，并同时观察曲线的变化。
　　② 当我们调小比例系数之后，曲线的大幅度振荡现象消失，但是曲线依旧存在小幅度的超调现象，并且此时通过调节比例系数已经无法优化曲线，如下图所示：

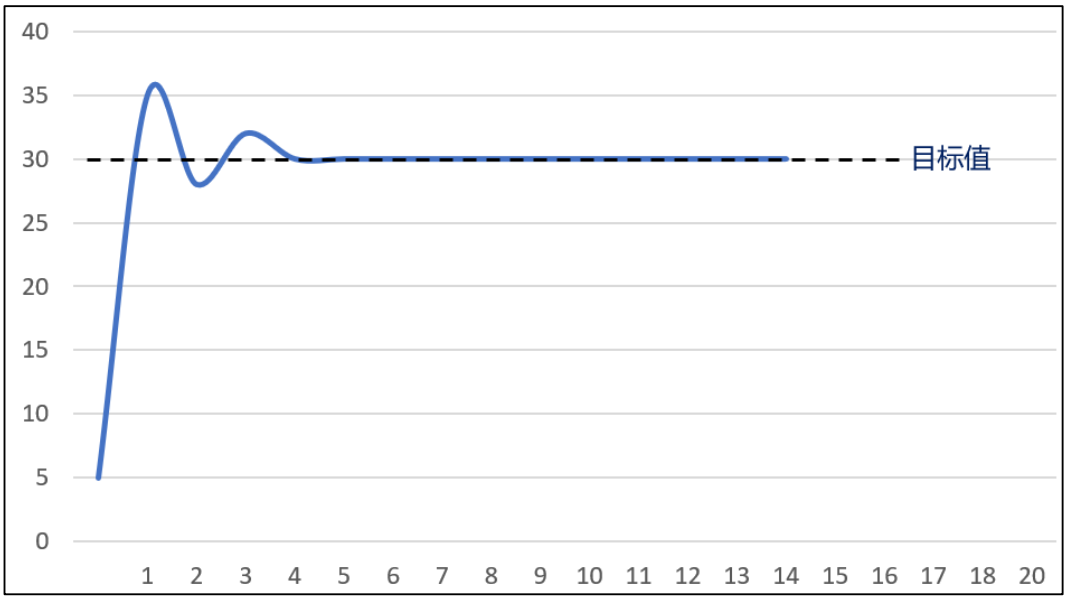
 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　PID 曲线存在小幅度超调

　　此时，我们可以慢慢地增大微分系数，并同时观察曲线的变化，从而找到最合适的参数。增大微分系数之后，如果系统的曲线已经较为理想，则说明这个系统只需要比例和微分环节的控制。
　　③ 如果在纯比例环节的控制下，系统的实际值始终达不到目标值，存在静态误差，如下图所示：

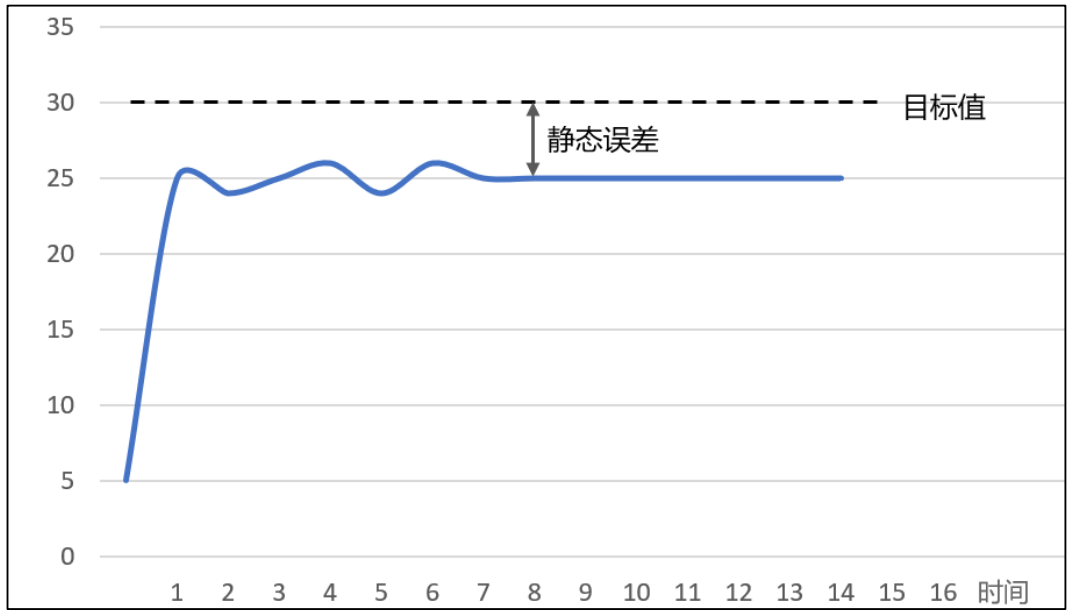
　　此时，我们可以逐渐增大积分系数，并同时观察曲线的变化，如果消除静差的时间过长，则可以再适当增大积分系数，但是需要注意兼顾系统的超调量。经过调整之后，如果系统的曲线已经较为理想，则说明这个系统只需要比例和积分环节的控制。
　　④ 如果系统在比例和积分环节的控制下出现小幅度的超调现象， 此时，我们可以慢慢地增大微分系数，并同时观察曲线的变化，从而找到最合适的参数。
　　以上就是在实际调参中经常遇到的一些问题以及解决方法。然而，在实际应用中，控制系统是多样且复杂的，上述方法只能作为参考，并不是通用的，因此在 PID 调参过程中，大家一定要注意经验的积累。

 3、PID积分饱和问题

　　在位置式 PID 中，如果系统长时间无法达到目标值，累计偏差（积分）就会变得很大，此时系统的响应就很慢了。 我们以一个实例来分析这个问题：
　　假设某个电机能达到的最大速度为 300RPM，而我们设置了目标速度为 350RPM，这明显是一个不合理的目标值，此时 PID 控制系统的曲线如下图所示：

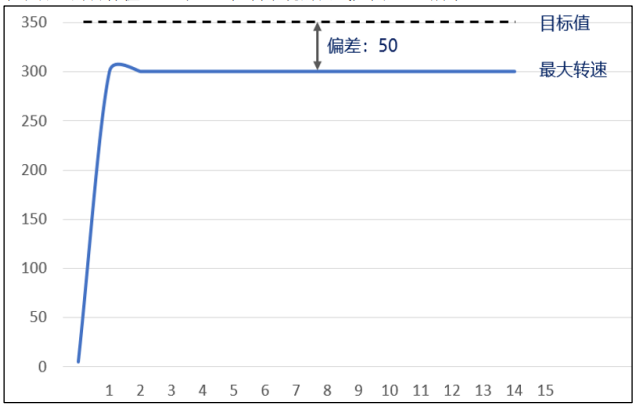
 　　　　　　　　　　　　　　不合理目标值

　　上图中，由于系统长时间无法达到目标值，累计偏差（积分）会变得越来越大，逐渐达到深度饱和的状态，此时我们再设置一个合理范围的目标速度（例如 200RPM），系统就没有办法在短时间内响应了。
　　为了避免位置式 PID 中可能出现的积分饱和问题，可采取以下措施：
　　　　① 优化 PID 曲线，系统越快达到目标值，累计的偏差就越小；
　　　　② 限制目标值调节范围，规避可以预见的偏差；
　　　　③ 进行积分限幅，在调整好 PID 系数之后，根据实际系统来选择限幅范围。

4、转发一些调试方法

https://cloud.tencent.com/developer/article/2095472