高一下三月日记

时间错乱

闲话

返校后一直在机房补 \(whk\) ，除了英语所有和语文年前的课程都补了。
某个晚上下课时间突然从 \(22:10\) 调整到了 \(21:40\) ，但机房众人都不知道这件事情，和 \(field\) 交涉未果遂直接润了。到宿舍后才发现因省里要求下课时间得到了调整，但要接着在宿舍学习半个小时来弥补差的时间。
学考报名的时候因和报名机房挨得比较近，所以 \(miaomiao\) 和那边的老师沟通了下，让我们先报了名，故准考证号都特别靠前；把身份证落在宿舍了，被迫回宿舍再去拿，期间 \(huge\) 怕宿管不给开门还单独写了份申请书让我带去，但并没用上。

3.15

闲话

做题纪要

luogu P11197 [COTS 2021] 赛狗游戏 Tiket

单 \(\log\) 求解三维偏序

设 \(S_{1}=\{ (i,j) | a_{i}<a_{j} \},S_{2}=\{ (i,j) | b_{i}<b_{j} \},S_{3}=\{ (i,j) | c_{i}<c_{j} \}\) ，考虑 \(|S_{1} \bigcap S_{2}|+|S_{1} \bigcap S_{3}|+|S_{2} \bigcap S_{3}|\) 中点对的贡献。
对于一组三维偏序，其被计算了三遍；对于一组只有两维满足偏序，其被计算了一遍；对于一组只有一维或零维满足偏序，其没有被计算到。
而若 \((i,j)\) 构成一组三维偏序，则 \((j,i)\) 构成零维偏序；若 \((i,j)\) 构成一组二维偏序，则 \((j,i)\) 构成一维偏序。即满足三维偏序和只有二维偏序的数对之和恰好是所有数对的一半 \(\frac{n(n-1)}{2}\) 。
故最后 \(\frac{1}{2}(|S_{1} \bigcap S_{2}|+|S_{1} \bigcap S_{3}|+|S_{2} \bigcap S_{3}|-\frac{n(n-1)}{2})\) 即为所求。

点击查看代码

ll a[500010],b[500010],c[500010],p[500010];
struct BIT
{
	ll c[500010];
	ll lowbit(ll x)
	{
		return (x&(-x));
	}
	void clear()
	{
		memset(c,0,sizeof(c));
	}
	void add(ll n,ll x,ll val)
	{
		for(ll i=x;i<=n;i+=lowbit(i))  c[i]+=val;
	}
	ll getsum(ll x)
	{
		ll ans=0;
		for(ll i=x;i>=1;i-=lowbit(i))  ans+=c[i];
		return ans;
	}
}T;
bool cmpa(ll x,ll y)
{
	return a[x]<a[y];
}
bool cmpc(ll x,ll y)
{
	return c[x]<c[y];
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,ans,x,i;
	scanf("%lld",&n);  ans=-n*(n-1)/2;
	for(i=1;i<=n;i++)
	{
		scanf("%lld",&x);  p[i]=i;
	}
	for(i=1;i<=n;i++)  
	{
		scanf("%lld",&x);  a[x]=i;
	}
	for(i=1;i<=n;i++)  
	{
		scanf("%lld",&x);  b[x]=i;
	}
	for(i=1;i<=n;i++)  
	{
		scanf("%lld",&x);  c[x]=i;
	}
	sort(p+1,p+1+n,cmpa);
	for(i=1;i<=n;i++)  
	{
		ans+=T.getsum(b[p[i]]-1);  T.add(n,b[p[i]],1);
	}
	T.clear();
	for(i=1;i<=n;i++)  
	{
		ans+=T.getsum(c[p[i]]-1);  T.add(n,c[p[i]],1);
	}
	T.clear();
	sort(p+1,p+1+n,cmpc);
	for(i=1;i<=n;i++)  
	{
		ans+=T.getsum(b[p[i]]-1);  T.add(n,b[p[i]],1);
	}
	printf("%lld\n",ans/2);
	return 0;
}

3.18

闲话

做题纪要

luogu P5353 树上后缀排序

树上后缀排序

字符串拼接可以树上倍增替代。
但是在树上可能会存在完全相等的字符串，需要额外对父亲排名和自己编号作为关键字进行排序。
额外以上一轮的有序状态作为第三关键字，开一个额外数组处理 \(rk\) 数组会出现重复的数的情况，跑两遍基数排序即可。

点击查看代码

struct node
{
	int nxt,to;
}e[500010];
int head[500010],fa[500010],pos[500010],cnt=0,tot=0;
char s[500010];
void add(int u,int v)
{
	cnt++;  e[cnt]=(node){head[u],v};  head[u]=cnt;
}
void dfs(int x)
{
	tot++;   pos[tot]=x;
	for(int i=head[x];i!=0;i=e[i].nxt)  dfs(e[i].to);
}
struct SA
{
	int sa[500010],rk[500010],_rk[500010],oldrk[500010],cnt[500010],id[500010],key[500010];
	int val(char x)
	{
		return (int)x;
	}
	void counting_sort(int n,int m,int sa[],int rk[],int id[])
	{
		memset(cnt,0,sizeof(cnt));
		for(int i=1;i<=n;i++)  
		{
			key[i]=rk[id[i]];  cnt[key[i]]++;
		}
		for(int i=1;i<=m;i++)  cnt[i]+=cnt[i-1];
		for(int i=n;i>=1;i--)
		{
			sa[cnt[key[i]]]=id[i];
			cnt[key[i]]--;
		}
	}
	void init(char s[],int len)
	{
		int m=127,tot=0;
		for(int i=1;i<=len;i++)
		{
			rk[i]=val(s[i]);  id[i]=i;
		}
		counting_sort(len,m,sa,rk,id);
		for(int i=1;i<=len;i++)  oldrk[i]=rk[i];
		tot=0;
		for(int i=1;i<=len;i++)
		{
			tot+=(oldrk[sa[i]]!=oldrk[sa[i-1]]);
			rk[sa[i]]=tot;  _rk[sa[i]]=i;
		}
		for(int w=0;w<=__lg(len);w++,m=tot)
		{
			for(int i=1;i<=len;i++)  oldrk[i]=_rk[fa[i]];
			counting_sort(len,len,id,oldrk,sa);  counting_sort(len,m,sa,rk,id);
			for(int i=1;i<=len;i++)  oldrk[i]=rk[i];
			tot=0;
			for(int i=1;i<=len;i++)
			{
				tot+=(oldrk[sa[i]]!=oldrk[sa[i-1]]||oldrk[fa[sa[i]]]!=oldrk[fa[sa[i-1]]]);
				rk[sa[i]]=tot;  _rk[sa[i]]=i;
			}
			for(int i=len;i>=1;i--)  fa[pos[i]]=fa[fa[pos[i]]];
		}
	}
}S;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,i;
	cin>>n;
	for(i=2;i<=n;i++) 
	{
		cin>>fa[i];  add(fa[i],i);
	}
	cin>>(s+1);  
	dfs(1);  S.init(s,n);
	for(i=1;i<=n;i++)  cout<<S.sa[i]<<" ";
	return 0;
}

luogu B4243 [语言月赛 202503] 长方形

顺序结构。

点击查看代码

int a,b,s;
cin>>a>>s;  b=s/a;
cout<<2*(a+b)<<endl;

luogu B4244 [语言月赛 202503] 水流

分支结构。

点击查看代码

int a,b,c;
cin>>a>>b>>c;
if(a>b)  cout<<((c<a)?"LeftToRight":"None")<<endl;
if(a==b)  cout<<"None"<<endl;
if(a<b)  cout<<((c<b)?"RightToLeft":"None")<<endl;

luogu B4245 [语言月赛 202503] 格式转换器

循环结构。

点击查看代码

int n,x,i;
cin>>n;
for(i=1;i<=n;i++)
{
	cin>>x;
	cout<<x;
	if(i!=n)  cout<<",";
}

luogu B4246 [语言月赛 202503] 环形游走

编号 \(-1\) 方便代码实现。

点击查看代码

int n,m,x=0,i;
cin>>n>>m;
for(i=0;i<=n-1;i++)  cin>>a[i];
for(i=1;i<=m;i++)  x=((x-a[x])%n+n)%n;
cout<<x+1<<endl;

luogu B4247 [语言月赛 202503] 半个哥德巴赫猜想

筛法。

点击查看代码

int prime[100010],vis[100010],ins[100010],len=0;
void isprime(int n)
{
	memset(vis,0,sizeof(vis));
	for(int i=2;i<=n;i++)
	{
		if(vis[i]==0)
		{
			len++;
			prime[len]=i;
		}
		for(int j=1;j<=len&&i*prime[j]<=n;j++)
		{
			vis[i*prime[j]]=true;
			if(i%prime[j]==0)
			{
				break;
			}
		}
	}
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,ans=0,minn=0x3f3f3f3f,i,j;
	cin>>n;  isprime(n);
	for(i=2;i*i<=n;i++)
	{
		for(j=1;j*i*i<=n;j++)  ins[j*i*i]=1;
	}
	for(i=1;i<=len;i++)
	{
		if(ins[n-prime[i]]==1)
		{
			ans++;
			minn=min(minn,abs(n-prime[i]-(prime[i])));
		}
	}
	cout<<ans<<endl<<minn<<endl;
	return 0;
}

luogu B4248 [语言月赛 202503] 数字棋盘

循环结构。

点击查看代码

const int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
int a[1010][1010];
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,x,y,ans=0,flag,i,j,k;
	cin>>n>>m;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)  cin>>a[i][j];
	}
	cin>>x>>y;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
		{
			if(a[i][j]==x)
			{
				flag=0;
				for(k=0;k<=3;k++)  flag|=(1<=i+dx[k]&&i+dx[k]<=n&&1<=j+dy[k]&&j+dy[k]<=m&&a[i+dx[k]][j+dy[k]]==y);
				ans+=flag;
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}

3.19

闲话

做题纪要

luogu B4249 [语言月赛 202503] 洗牌

deque 模拟。

点击查看代码

deque<string>q,l,r;
string s,t;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,i;
	char c;
	cin>>n>>s;
	for(i=0;i<s.size();i++)
	{
		if(s[i]==',')
		{
			q.push_back(t);
			t="";
		}
		else  t+=s[i];
	}
	q.push_back(t);
	for(i=1;i<=n;i++)
	{
		l.push_back(q.front());   q.pop_front();
	}
	swap(r,q);
	for(i=1;i<=2*n;i++)
	{
		cin>>c;
		if(c=='L')
		{
			q.push_back(l.front());
			l.pop_front();
		}
		else
		{
			q.push_back(r.front());
			r.pop_front();
		}
	}
	for(i=1;i<=2*n;i++)
	{
		if(i%2==1)  cout<<q.back()<<endl;
		q.pop_back();
	}
	return 0;
}

luogu B4250 [语言月赛 202503] 蛋挞制作工坊

循环结构。

点击查看代码

struct node
{
	int r,num,id;
}c[110][110];
int g[110];
bool cmp(node a,node b)
{
	if(a.r!=b.r)  return a.r<b.r;
	if(a.num!=b.num)  return a.num>b.num;
	return a.id<b.id;
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,minn,i,j;
	cin>>n>>m;
	for(i=1;i<=m;i++)  cin>>g[i];
	for(j=1;j<=n;j++)
	{
		minn=0x7f7f7f7f;
		for(i=1;i<=m;i++)
		{
			cin>>c[i][j].r;  c[i][j].id=j;
			minn=min(minn,c[i][j].r/g[i]);
		}
		for(i=1;i<=m;i++)
		{
			c[i][j].num=minn;  c[i][j].r-=minn*g[i];
		}
	}
	for(i=1;i<=m;i++)
	{
		sort(c[i]+1,c[i]+1+n,cmp);
		for(j=1;j<=n;j++)  cout<<c[i][j].id<<" ";
		cout<<endl;
	}
	return 0;
}

3.21

闲话

做题纪要

luogu P11830 [省选联考 2025] 幸运数字

假设我们需要对 \(mid\) 进行 \(check\) 。我们只关心 \(<mid,=mid,>mid\) 的数的个数，不妨分别设为 \(a,b,c\) 。
带着 \(\left\lfloor \dfrac{m+1}{2} \right\rfloor\) 的限制很难处理，考虑中位数的本质转化为 \(a,b,c\) 的大小关系。
此时有 \(a+b \ge c,a<b+c\) ， \(b\) 肯定是越大越好，遂只需要解决 \(a,c\) 的取值范围。
容易得到 \(c \in [\operatorname{down}(a)-b+1,\operatorname{up}(a)]\) 与 \([\operatorname{down}(c),\operatorname{up}(c)]\) 判断有没有交即可。
具体实现时，可以对值域划分成若干段区间进行差分，且一段区间只要有一个数合法就全部合法。

注意划分区间时产生的空区间的处理。

点击查看代码

const ll inf=1000000000;
ll l[2][400010],r[2][400010],s[6][400010];
vector<ll>d;
bool check(ll sl,ll _sl,ll sq,ll sr,ll _sr,ll sum)
{
	return max(sl-sq+1,sr)<=min(_sl+sq,_sr)&&sum>=1;
}
int main()
{
#define Isaac
#ifdef Isaac
	freopen("lucky.in","r",stdin);
	freopen("lucky.out","w",stdout);
#endif
	ll c,t,n,ans,pos,i,j;
	scanf("%lld%lld",&c,&t);
	for(;t>=1;t--)
	{
		scanf("%lld",&n);  ans=0;
		memset(s,0,sizeof(s));
		d.clear();  d.push_back(1);
		for(i=1;i<=n;i++)
		{
			scanf("%lld%lld%lld%lld",&l[0][i],&r[0][i],&l[1][i],&r[1][i]);
			d.push_back(l[1][i]);  d.push_back(r[1][i]+1);
		}
		d.push_back(inf+1);
		sort(d.begin(),d.end());  d.erase(unique(d.begin(),d.end()),d.end());
		for(i=1;i<=n;i++)
		{
			pos=lower_bound(d.begin(),d.end(),l[1][i])-d.begin();  s[2][pos]+=r[0][i];  s[5][pos]++;
			if(l[1][i]-1>=1)
			{
				s[3][pos]-=l[0][i];  s[4][pos]-=r[0][i];
				s[3][0]+=l[0][i];  s[4][0]+=r[0][i];
			}
			pos=lower_bound(d.begin(),d.end(),r[1][i]+1)-d.begin();  s[2][pos]-=r[0][i];  s[5][pos]--;
			if(r[1][i]+1<=inf)
			{
				s[0][pos]+=l[0][i];  s[1][pos]+=r[0][i];
			}
		}
		for(j=0;j<=5;j++)  for(i=0;i<d.size();i++)  s[j][i]+=s[j][i-1];
		for(i=0;i+1<d.size();i++)  ans+=check(s[0][i],s[1][i],s[2][i],s[3][i],s[4][i],s[5][i])*(d[i+1]-d[i]);
		printf("%lld\n",ans);
	}
	return 0;
}

牛客 NC288381 智乃的天平

分支结构。

点击查看代码

ll a,b,w;
cin>>a>>b>>w;
if(w==a||w==b||w==a+b||w+a==b||w+b==a)  cout<<"Yes"<<endl;
else  cout<<"No"<<endl;

牛客 NC288383 智乃爬山

循环结构。

点击查看代码

int n,ans=-1,i;
cin>>n;
for(i=1;i<=n;i++)  cin>>a[i];
for(i=2;i<=n-1;i++)  if(a[i-1]<a[i]&&a[i]>a[i+1])  ans=max(ans,a[i]-(int)((a[i-1]+a[i+1])/2));
cout<<ans<<endl;

牛客 NC288388 智乃放球

手动解一下合法条件为 \((n-q) \equiv 0 \pmod{k} \land m(k-1) \ge q\) 。

点击查看代码

ll t,n,m,k,q,i;
cin>>t;
for(i=1;i<=t;i++)
{
	cin>>n>>m>>k>>q;
	if((n-q)%k==0&&m*(k-1)>=q)  cout<<"Yes"<<endl;
	else  cout<<"No"<<endl;
}

牛客 NC288385 智乃的“K”叉树

诈骗题。根节点变化至多影响 \(2\) 个点的孩子个数。

点击查看代码

int pre[100010],suf[100010],du[100010];
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,ans=0x3f3f3f3f,pos=0,u,v,i;
	cin>>n;
	for(i=1;i<=n-1;i++)  
	{
		cin>>u>>v;  
		du[u]++;  du[v]++;
	}
	for(i=1;i<=n;i++)  pre[i]=max(pre[i-1],du[i]-1);
	for(i=n;i>=1;i--)  suf[i]=max(suf[i+1],du[i]-1);
	for(i=1;i<=n;i++)
	{
		if(max({pre[i-1],suf[i+1],du[i]})<ans&&max({pre[i-1],suf[i+1],du[i]})>=1)
		{
			ans=max({pre[i-1],suf[i+1],du[i]});
			pos=i;
		}
	}
	cout<<ans<<" "<<pos<<endl;
	return 0;
}

3.22

闲话

做题纪要

luogu P3588 [POI 2015] PUS

连边表示大小关系，线段树优化建图，虚点连接。

拓扑辅助转移。

点击查看代码

int a[1000010],leaf[1000010],x[1000010],f[1000010],din[1000010],n;
vector<pair<int,int> >e[1000010];
void add(int u,int v,int w)
{
	din[v]++;
	e[u].push_back(make_pair(v,w));
}
struct SMT_Q_BG
{
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void build(int rt,int l,int r)
	{
		if(l==r)  
		{
			leaf[l]=rt;
			return;
		}
		add(rt,lson(rt),0);  add(rt,rson(rt),0);
		int mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
	}
	void update(int rt,int l,int r,int x,int y,int pos)
	{
		if(x<=l&&r<=y)
		{
			add(pos,rt,1);
			return;
		}
		int mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,pos);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,pos);
	}
}T;
bool top_sort(int n)
{
	int tot=0;
	queue<int>q;
	for(int i=1;i<=n;i++)  if(din[i]==0)  q.push(i);
	for(int i=1;i<=n;i++)  if(f[i]==0)  f[i]=1000000000;
	while(q.empty()==0)
	{
		tot++;
		int x=q.front();  q.pop();
		for(int i=0;i<e[x].size();i++)
		{
			if(f[x]-e[x][i].second<=0||f[x]-e[x][i].second<a[e[x][i].first])  return false;
			f[e[x][i].first]=min(f[e[x][i].first],f[x]-e[x][i].second);
			din[e[x][i].first]--;
			if(din[e[x][i].first]==0)  q.push(e[x][i].first);
		}
	}
	return (tot==n);
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int s,m,l,r,k,i,j;
	cin>>n>>s>>m;  T.build(1,1,n);
	for(i=1;i<=s;i++)
	{
		cin>>l;  cin>>a[leaf[l]];
		f[leaf[l]]=a[leaf[l]];
	} 
	for(i=1;i<=m;i++)
	{
		cin>>l>>r>>k;
		x[0]=l-1;  x[k+1]=r+1;
		for(j=1;j<=k;j++)
		{
			cin>>x[j];
			add(leaf[x[j]],8*n+i,0);
		}
		for(j=0;j<=k;j++)  if(x[j]+1<=x[j+1]-1)  T.update(1,1,n,x[j]+1,x[j+1]-1,8*n+i);
	}
	if(top_sort(8*n+m)==true)
	{
		cout<<"TAK"<<endl;
		for(i=1;i<=n;i++)  cout<<f[leaf[i]]<<" ";
	}
	else  cout<<"NIE"<<endl;
	return 0;
}

HDU6087 Rikka with Sequence

将 \(a\) 复制一遍接在后面此时操作 \(3\) 就转化成了区间复制，考虑可持久化平衡树。
乍一看操作 \(2\) 也是个区间复制，但实际不然。
倍增复制 \([l-k,l-1]\) 直至长度 \(\ge r-l+1\) 即可。

需要定期重构。

点击查看代码

int a[400010],top=0;
struct PDS_BST
{
	int root,rt_sum;
	struct FHQ_Treap
	{
		int son[2],val,siz;
		ll sum;
	}tree[2300010];
	#define lson(rt) (tree[rt].son[0])
	#define rson(rt) (tree[rt].son[1])
	PDS_BST()
	{
		rt_sum=0;
		srand(time(0));
	}
	int build_rt(int val)
	{
		rt_sum++;
		lson(rt_sum)=rson(rt_sum)=0;
		tree[rt_sum].val=tree[rt_sum].sum=val;
		tree[rt_sum].siz=1;
		return rt_sum;
	}
	int copy_rt(int rt)
	{
		rt_sum++;
		tree[rt_sum]=tree[rt];
		return rt_sum;
	}
	void pushup(int rt)
	{
		tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+1;
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum+tree[rt].val;
	}
	int merge(int rt1,int rt2)
	{
		if(rt1==0||rt2==0)  return rt1+rt2;
		int rt;
		if(rand()%(tree[rt1].siz+tree[rt2].siz)<tree[rt1].siz)
		{
			rt=copy_rt(rt1);
			rson(rt)=merge(rson(rt),rt2);
		}
		else
		{
			rt=copy_rt(rt2);
			lson(rt)=merge(rt1,lson(rt));
		}
		pushup(rt);
		return rt;
	}
	void split(int rt,int k,int &x,int &y)
	{
		if(rt==0)
		{
			x=y=0;
			return;
		}
		if(tree[lson(rt)].siz+1<=k)
		{
			x=copy_rt(rt);
			split(rson(rt),k-tree[lson(rt)].siz-1,rson(x),y);
			pushup(x);
		}
		else
		{
			y=copy_rt(rt);
			split(lson(rt),k,x,lson(y));
			pushup(y);
		}
	}
	ll query(int l,int r)
	{
		ll ans=0;
		int x,y,z;
		split(root,r,x,y);
		split(x,l-1,x,z);
		ans=tree[z].sum;
		root=merge(merge(x,z),y);
		return ans;
	}
	void update(int l,int r,int k)
	{
		int x,y,z,_x,_z;
		split(root,r,x,y);
		split(x,l-1,x,z);  _x=x;
		split(x,l-k-1,x,_z);
		while(tree[_z].siz<r-l+1)  _z=merge(_z,_z);
		split(_z,r-l+1,_z,z);
		root=merge(merge(_x,_z),y);
	}
	void paste(int l1,int r1,int l2,int r2)
	{
		int x,y,z,_y,_z;
		split(root,r2,x,y);
		split(x,l2-1,x,z);
		split(root,r1,_y,_z);
		split(_y,l1-1,_y,_z);
		root=merge(merge(x,_z),y);
	}
	void dfs(int rt)
	{
		if(rt==0)  return;
		dfs(lson(rt));
		a[++top]=tree[rt].val;
		dfs(rson(rt));
	}
	void build(int &rt,int l,int r)
	{
		if(l>r)  
		{
			rt=0;
			return;
		}
		int mid=(l+r)/2;
		rt=build_rt(a[mid]);
		build(lson(rt),l,mid-1);  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	void rebuild(int n)
	{
		if(rt_sum>1800000)
		{
			top=0;   dfs(root);
			rt_sum=0;build(root,1,n);
		}
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,pd,l,r,x,i;
	cin>>n>>m;
	for(i=1;i<=n;i++)  
	{
		cin>>a[i];  a[n+i]=a[i];
	}
	T.build(T.root,1,2*n);
	for(i=1;i<=m;i++)
	{
		cin>>pd>>l>>r;
		if(pd==1)  cout<<T.query(l,r)<<endl;
		if(pd==2)
		{
			cin>>x;  T.update(l,r,x);
		}
		if(pd==3)  T.paste(l+n,r+n,l,r);
		T.rebuild(2*n);
	}
	return 0;
}

CF603E Pastoral Oddities

通过 \(|E|=\dfrac{\sum\limits d_{i}}{2}\) 可知当存在一个连通块大小为奇数时一定不合法。
当连通块大小均为偶数时，可以通过在生成树上自下而上连边得到一组可行解，本质上是一个类似树上最大匹配的过程。
将边权升序排序后考虑从小到大加边。贪心地考虑一下决策后得到在存在奇大小的连通块的情况下，如果连边能减少连通块数则连边一定不劣。

所以每条边对答案产生贡献的是一段区间，考虑线段树分治，自右向左经过叶子节点的途中进行加边。

点击查看代码

struct quality
{
	int id,fa,siz,delta;
};
int u[300010],v[300010],w[300010],p[300010],ans[300010],m,cur=1;
bool cmp(int x,int y)
{
	return w[x]<w[y];
}
struct DSU
{
	int fa[100010],siz[100010],sum;
	void init(int n)
	{
		sum=n;
		for(int i=1;i<=n;i++)
		{
			fa[i]=i;  siz[i]=1;
		}
	}
	int find(int x)
	{
		return fa[x]==x?x:find(fa[x]);
	}
	void merge(int x,int y,stack<quality>&s)
	{
		x=find(x);  y=find(y);
		if(x!=y)
		{
			if(siz[x]>siz[y])  swap(x,y);
			s.push((quality){x,fa[x],siz[x],(siz[x]%2==1&&siz[y]%2==1)});
			s.push((quality){y,fa[y],siz[y],(siz[x]%2==1&&siz[y]%2==1)});
			sum-=(siz[x]%2==1&&siz[y]%2==1)*2;
			fa[x]=y;  siz[y]+=siz[x];
		}
	}
	void split(stack<quality>&s)
	{
		while(s.empty()==0)
		{
			fa[s.top().id]=s.top().fa;
			siz[s.top().id]=s.top().siz;
			sum+=s.top().delta;
			s.pop();
		}
	}
}D;
struct SMT
{
	vector<int>tree[1200010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void update(int rt,int l,int r,int x,int y,int id)
	{
		if(x<=l&&r<=y)
		{
			tree[rt].push_back(id);
			return;
		}
		int mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,id);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,id);
	}
	void solve(int rt,int l,int r)
	{
		stack<quality>s;
		int mid=(l+r)/2;
		for(int i=0;i<tree[rt].size();i++)  D.merge(u[tree[rt][i]],v[tree[rt][i]],s);
		if(l==r)
		{
			for(;cur<=m;cur++)
			{
				if(p[cur]<=l)
				{
					D.merge(u[p[cur]],v[p[cur]],s);
					if(p[cur]<=l-1)  update(1,1,m,p[cur],l-1,p[cur]);//为保证能够成功下传遂写的是到 l-1
				}
				if(D.sum==0)
				{
					ans[l]=w[p[cur]];
					break;
				}
			}
		}
		else
		{
			solve(rson(rt),mid+1,r);  solve(lson(rt),l,mid);
		}
		D.split(s);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,i;
	cin>>n>>m;  D.init(n);
	for(i=1;i<=m;i++)  
	{
		cin>>u[i]>>v[i]>>w[i];  p[i]=i;  ans[i]=-1;
	}
	sort(p+1,p+1+m,cmp);  T.solve(1,1,m);
	for(i=1;i<=m;i++)  cout<<ans[i]<<endl;
	return 0;
}

luogu P5579 [PA 2015] Siano

容易发现任一时刻生长速度快的一定比生长速度慢的高度高。
按照 \(a_{i}\) 升序排序后割掉的草就是一段后缀，线段树二分维护即可。

具体地，同时打上区间覆盖和对 \(t\) 的懒惰标记即可。

点击查看代码

ll a[500010],x[500010],y[500010];
struct SMT
{
	struct SegmentTree
	{
		ll k,sum,maxx,add,cov;
	}tree[2000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void pushup(ll rt)
	{
		tree[rt].k=tree[lson(rt)].k+tree[rson(rt)].k;
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum;
		tree[rt].maxx=max(tree[lson(rt)].maxx,tree[rson(rt)].maxx);
	}
	void build(ll rt,ll l,ll r)
	{
		tree[rt].sum=tree[rt].maxx=tree[rt].add=0;
		tree[rt].cov=-1;
		if(l==r)  
		{
			tree[rt].k=a[l];
			return;
		}
		ll mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	void pushlazy(ll rt,ll l,ll r,ll add,ll cov)
	{
		if(cov!=-1)
		{
			tree[rt].maxx=tree[rt].cov=cov;
			tree[rt].sum=(r-l+1)*cov;
			tree[rt].add=0;
		}
		if(add!=0)
		{
			tree[rt].add+=add;
			tree[rt].sum+=tree[rt].k*add;
			tree[rt].maxx+=a[r]*add;
		}
	}
	void pushdown(ll rt,ll l,ll r,ll mid)
	{
		pushlazy(lson(rt),l,mid,tree[rt].add,tree[rt].cov);
		pushlazy(rson(rt),mid+1,r,tree[rt].add,tree[rt].cov);
		tree[rt].add=0;  tree[rt].cov=-1;
	}
	ll update(ll rt,ll l,ll r,ll val)
	{
		ll sum=tree[rt].sum;
		pushlazy(rt,l,r,0,val);
		return sum-tree[rt].sum;
	}
	ll query(ll rt,ll l,ll r,ll val)
	{
		if(tree[rt].maxx<val)  return 0;
		if(l==r)  return update(rt,l,r,val);
		ll mid=(l+r)/2,ans;
		pushdown(rt,l,r,mid);
		if(tree[lson(rt)].maxx>=val)  ans=query(lson(rt),l,mid,val)+update(rson(rt),mid+1,r,val);
		else  ans=query(rson(rt),mid+1,r,val);
		pushup(rt);
		return ans;
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,i;
	scanf("%lld%lld",&n,&m);
	for(i=1;i<=n;i++)  scanf("%lld",&a[i]);
	sort(a+1,a+1+n);  T.build(1,1,n);
	for(i=1;i<=m;i++)
	{
		scanf("%lld%lld",&x[i],&y[i]);  T.pushlazy(1,1,n,x[i]-x[i-1],-1);
		printf("%lld\n",T.query(1,1,n,y[i]));
	}
	return 0;
}

HDU5306 Gorgeous Sequence

延续 luogu P4560 [IOI 2014] Wall 砖墙的做法的话，打标记无法快速对区间和进行更新。
对于线段树上每个区间 \([l,r]\) ，额外维护最大值 \(mx\) ，严格次大值 \(se\) 及最大值个数 \(cnt\) 。假设当前要对 \(x\) 取 \(\min\) 。
- 若 \(mx \le x\) 时本次操作不会对其产生影响，直接退出。
- 若 \(se<x<mx\) 时本次修改只会影响到所有最大值，将 \(sum\) 减去 \(cnt(mx-x)\) ，再打上覆盖的标记后退出。
- 若 \(se \ge x\) 时无法直接更新，需要进一步进行区间定位直至符合上面两种情况之一。

由势能分析可知时间复杂度为 \(O(m \log n)\) ，略带卡常。

点击查看代码

namespace IO{
	#ifdef LOCAL
	FILE*Fin(fopen("test.in","r")),*Fout(fopen("test.out","w"));
	#else
	FILE*Fin(stdin),*Fout(stdout);
	#endif
	class qistream{static const size_t SIZE=1<<16,BLOCK=64;FILE*fp;char buf[SIZE];int p;public:qistream(FILE*_fp=stdin):fp(_fp),p(0){fread(buf+p,1,SIZE-p,fp);}void flush(){memmove(buf,buf+p,SIZE-p),fread(buf+SIZE-p,1,p,fp),p=0;}qistream&operator>>(char&x){x=getch();while(isspace(x))x=getch();return*this;}template<class T>qistream&operator>>(T&x){x=0;p+BLOCK>=SIZE?flush():void();bool flag=false;for(;!isdigit(buf[p]);++p)flag=buf[p]=='-';for(;isdigit(buf[p]);++p)x=x*10+buf[p]-'0';x=flag?-x:x;return*this;}char getch(){p+BLOCK>=SIZE?flush():void();return buf[p++];}qistream&operator>>(char*str){char ch=getch();while(ch<=' ')ch=getch();int i=0;for(;ch>' ';++i,ch=getch())str[i]=ch;str[i]='\0';return*this;}}qcin(Fin);
	class qostream{static const size_t SIZE=1<<16,BLOCK=64;FILE*fp;char buf[SIZE];int p;public:qostream(FILE*_fp=stdout):fp(_fp),p(0){}~qostream(){fwrite(buf,1,p,fp);}void flush(){fwrite(buf,1,p,fp),p=0;}template<class T>qostream&operator<<(T x){int len=0;p+BLOCK>=SIZE?flush():void();x<0?(x=-x,buf[p++]='-'):0;do buf[p+len]=x%10+'0',x/=10,++len;while(x);for(int i=0,j=len-1;i<j;++i,--j)std::swap(buf[p+i],buf[p+j]);p+=len;return*this;}qostream&operator<<(char x){putch(x);return*this;}void putch(char ch){p+BLOCK>=SIZE?flush():void();buf[p++]=ch;}qostream&operator<<(char*str){for(int i=0;str[i];++i)putch(str[i]);return*this;}qostream&operator<<(const char*s){for(int i=0;s[i];++i)putch(s[i]);return*this;}}qcout(Fout);
}
#define cin IO::qcin
#define cout IO::qcout
int a[1000010];
struct SMT
{
	struct SegmentTree
	{
		int mx,se,cnt,cov;
		ll sum;
	}tree[4000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void pushup(int rt)
	{
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum;
		tree[rt].mx=max(tree[lson(rt)].mx,tree[rson(rt)].mx);
		if(tree[lson(rt)].mx>tree[rson(rt)].mx)
		{
			tree[rt].se=max(tree[lson(rt)].se,tree[rson(rt)].mx);
			tree[rt].cnt=tree[lson(rt)].cnt;
		}
		if(tree[lson(rt)].mx==tree[rson(rt)].mx)
		{
			tree[rt].se=max(tree[lson(rt)].se,tree[rson(rt)].se);
			tree[rt].cnt=tree[lson(rt)].cnt+tree[rson(rt)].cnt;
		}
		if(tree[lson(rt)].mx<tree[rson(rt)].mx)
		{
			tree[rt].se=max(tree[lson(rt)].mx,tree[rson(rt)].se);
			tree[rt].cnt=tree[rson(rt)].cnt;
		}
	}
	void pushlazy(int rt,int cov)
	{
		if(tree[rt].mx<=cov)  return;	
		tree[rt].sum-=1ll*tree[rt].cnt*(tree[rt].mx-cov);
		tree[rt].mx=tree[rt].cov=cov;
	}
	void pushdown(int rt)
	{
		if(tree[rt].cov!=-1)
		{
			pushlazy(lson(rt),tree[rt].cov);
			pushlazy(rson(rt),tree[rt].cov);
			tree[rt].cov=-1;
		}
	}
	void build(int rt,int l,int r)
	{
		tree[rt].cov=-1;
		if(l==r)
		{
			tree[rt].sum=tree[rt].mx=a[l];
			tree[rt].se=-1;  tree[rt].cnt=1;
			return;
		}
		int mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	void update(int rt,int l,int r,int x,int y,int val)
	{
		if(tree[rt].mx<=val)  return;
		if(x<=l&&r<=y&&tree[rt].se<val)
		{
			pushlazy(rt,val);
			return;
		}
		pushdown(rt);
		int mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,val);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	int query1(int rt,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)  return tree[rt].mx;
		pushdown(rt);
		int mid=(l+r)/2;
		if(y<=mid)  return query1(lson(rt),l,mid,x,y);
		if(x>mid)  return query1(rson(rt),mid+1,r,x,y);
		return max(query1(lson(rt),l,mid,x,y),query1(rson(rt),mid+1,r,x,y));
	}
	ll query2(int rt,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)  return tree[rt].sum;
		pushdown(rt);
		int mid=(l+r)/2;
		if(y<=mid)  return query2(lson(rt),l,mid,x,y);
		if(x>mid)  return query2(rson(rt),mid+1,r,x,y);
		return query2(lson(rt),l,mid,x,y)+query2(rson(rt),mid+1,r,x,y);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int t,n,m,pd,l,r,x,i;
	cin>>t;
	for(;t>=1;t--)
	{
		cin>>n>>m;
		for(i=1;i<=n;i++)  cin>>a[i];
		T.build(1,1,n);
		for(i=1;i<=m;i++)
		{
			cin>>pd>>l>>r;
			if(pd==0)
			{
				cin>>x;
				T.update(1,1,n,l,r,x);
			}
			if(pd==1)  cout<<T.query1(1,1,n,l,r)<<endl;
			if(pd==2)  cout<<T.query2(1,1,n,l,r)<<endl;
		}
	}
	return 0;
}

[ABC398A] Doors in the Center

循环结构。

点击查看代码

int n;
cin>>n;
for(int i=1;i<=n;i++)  s[i]='-';
if(n%2==0)
{
	s[n/2]=s[n/2+1]='=';
}
else
{
	s[n/2+1]='=';
}
printf("%s",s+1);

[ABC398B] Full House 3

只关心出现次数的最大值和非严格次大值即可。

点击查看代码

int a[10],cnt[20];
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int f=0,g=0,i;
	for(int i=1;i<=7;i++)
	{
		cin>>a[i];
		cnt[a[i]]++;
	}
	for(int i=1;i<=13;i++)
	{
		if(cnt[i]>f)
		{
			g=f;
			f=cnt[i];
		}
		else  g=max(g,cnt[i]);
	}
	if(f>=3&&g>=2)  cout<<"Yes"<<endl;
	else  cout<<"No"<<endl;
	return 0;
}

[ABC398C] Uniqueness

循环结构。

点击查看代码

int a[300010];
map<int,int>f;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,ans=-1,maxx=0,i;
	cin>>n;
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
		f[a[i]]++;
	}
	for(i=1;i<=n;i++)
	{
		if(f[a[i]]==1&&a[i]>maxx)
		{
			maxx=a[i];
			ans=i;
		}
	}
	cout<<ans<<endl;
	return 0;
}

[ABC398F] ABCBA

多部经验： UVA11475 Extend to Palindrome | SP4103 EPALIN - Extend to Palindrome | luogu P9606 [CERC2019] ABB

点击查看代码

int r[1000010];
string s,t=" #";
int main()
{
	int n,maxr=0,id=0,ans=0,i;
	cin>>s;
	for(i=0;i<s.size();i++)
	{
		t+=s[i];  t+="#";
	}
	n=t.size()-1;
	for(i=1;i<=n;i++)
	{
		r[i]=(i<maxr)?min(r[id-(i-id)],maxr-i):1;
		while(1<=i-r[i]&&i+r[i]<=n&&t[i-r[i]]==t[i+r[i]])  r[i]++;
		if(maxr<i+r[i])
		{
			maxr=i+r[i];
			id=i;
		}
		if(i+r[i]-1==n)
		{
			ans=r[i]-1;
			break;
		}
	}
	cout<<s;
	for(i=s.size()-1-ans;i>=0;i--)  cout<<s[i];
	cout<<endl;
	return 0;
}

[ABC398D] Bonfire

如果放到操作序列上考虑后缀和的贡献的话需要快速查询是否存在 \(1 \le p<q=i+1\) 使得 \(x_{p}-x_{q}=r,y_{p}-y_{q}=c\) ，可以将 \((x_{p},y_{p})\) 插进去后查询 \((x_{q}+r,y_{q}+r)\) 是否出现过，对相应的 \(i\) 进行贡献。

套路性地，不妨直接进行人和篝火（处理每次新出现的 \((0,0)\) 贡献）的移动，其实质仍是在操作序列 \([1,i]\) 中找到一组合法的后缀作为解。

点击查看代码

const int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};
map<pair<int,int>,int>f;
char s[200010];
int val(char x)
{
	if(x=='N')  return 0;
	if(x=='W')  return 1;
	if(x=='S')  return 2;
	return 3;
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,x,y,flag,p,q,i,j;
	cin>>n>>x>>y;  x+=n;  y+=n;
	p=q=n;  f[make_pair(p,q)]=1;
	scanf("%s",s+1);
	for(i=1;i<=n;i++)
	{
		p-=dx[val(s[i])];  x-=dx[val(s[i])];
		q-=dy[val(s[i])];  y-=dy[val(s[i])];
		f[make_pair(p,q)]=1;
		cout<<(f.find(make_pair(x,y))!=f.end());
	}
	return 0;
}

[ABC398E] Tree Game

能连的边有且仅有树上距离为奇数且 \(\ne 1\) 的点对，手摸后发现偶环套偶环还是偶环，无脑连上即可。

点击查看代码

// #define endl '\n'	
int dis[110][110];
set<pair<int,int> >s;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,u,v,i,j,k;
	cin>>n;
	memset(dis,0x3f,sizeof(dis));
	for(i=1;i<=n-1;i++)
	{
		cin>>u>>v;
		dis[u][v]=dis[v][u]=1;
	}
	for(k=1;k<=n;k++)
	{
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=n;j++)  
			{
				dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
			}
		}
	}
	for(i=1;i<=n;i++)
	{
		for(j=i+1;j<=n;j++)
		{
			if(dis[i][j]!=0x3f3f3f3f&&dis[i][j]!=1&&dis[i][j]%2==1)  s.insert(make_pair(i,j));
		}
	}
	if(s.size()%2==1)  
	{
		cout<<"First"<<endl;
		cout<<s.begin()->first<< " "<<s.begin()->second<<endl;
		s.erase(s.begin());
	}
	else  cout<<"Second"<<endl;
	while(s.empty()==0)
	{
		cin>>u>>v;  s.erase(make_pair(u,v));
		cout<<s.begin()->first<<" "<<s.begin()->second<<endl;
		s.erase(s.begin());
	}
	return 0;
}

3.23

闲话

做题纪要

luogu P10639 BZOJ4695 最佳女选手

同 luogu P8024 [ONTAK2015] Stumilowy sad ，考虑规定标记下传的优先级，不妨规定加法标记 \(>\) 取 \(\max\) 的标记 \(>\) 取 \(\min\) 的标记。
以对 \(x\) 取 \(\max\) 为例，若先前的标记为对 \(y\) 取 \(\min\) 且 \(y<x\) 那么在执行完这次操作后又全部都会变成 \(x\) ，需要同时更新取 \(\min\) 的标记 \(y \gets x\) 。
当维护数集重合时需要特殊处理最大值与最小值、次小值，最小值与最大值、次大值相同时的更改。

由势能分析可知时间复杂度为 \(o(m \log^{2} n)\) ，但实际表现良好。

点击查看代码

const ll inf=0x3f3f3f3f3f3f3f3f;
ll a[500010];
struct SMT
{
	struct quality
	{
		ll mo,se,cnt;
		quality operator + (const quality another) const
		{
			quality tmp;
			tmp.mo=max(mo,another.mo);
			if(mo>another.mo)
			{
				tmp.se=max(se,another.mo);
				tmp.cnt=cnt;
			}
			if(mo==another.mo)
			{
				tmp.se=max(se,another.se);
				tmp.cnt=cnt+another.cnt;
			}
			if(mo<another.mo)
			{
				tmp.se=max(mo,another.se);
				tmp.cnt=another.cnt;
			}
			return tmp;
		}
		quality operator - (const quality another) const
		{
			quality tmp;
			tmp.mo=min(mo,another.mo);
			if(mo<another.mo)
			{
				tmp.se=min(se,another.mo);
				tmp.cnt=cnt;
			}
			if(mo==another.mo)
			{
				tmp.se=min(se,another.se);
				tmp.cnt=cnt+another.cnt;
			}
			if(mo>another.mo)
			{
				tmp.se=min(mo,another.se);
				tmp.cnt=another.cnt;
			}
			return tmp;
		}
	};
	struct SegmentTree
	{
		ll sum,len,add,upward,downward;
		quality mx,mn;
	}tree[2000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void pushup(ll rt)
	{
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum;
		tree[rt].mx=tree[lson(rt)].mx+tree[rson(rt)].mx;
		tree[rt].mn=tree[lson(rt)].mn-tree[rson(rt)].mn;
	}
	void build(ll rt,ll l,ll r)
	{
		tree[rt].add=0;  tree[rt].upward=-inf;  tree[rt].downward=inf;
		tree[rt].len=r-l+1;
		if(l==r)
		{
			tree[rt].mx.mo=tree[rt].mn.mo=tree[rt].sum=a[l];
			tree[rt].mx.se=-inf;  tree[rt].mn.se=inf;
			tree[rt].mx.cnt=tree[rt].mn.cnt=1;
			return;
		}
		ll mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	void pushlazy(ll rt,ll add,ll upward,ll downward)
	{
		if(add!=0)
		{
			tree[rt].sum+=tree[rt].len*add;
			tree[rt].mx.mo+=add;  tree[rt].mn.mo+=add;
			if(tree[rt].mx.se!=-inf)  tree[rt].mx.se+=add;
			if(tree[rt].mn.se!=inf)  tree[rt].mn.se+=add;
			tree[rt].add+=add;
			if(tree[rt].upward!=-inf)  tree[rt].upward+=add;
			if(tree[rt].downward!=inf)  tree[rt].downward+=add;
		}
		if(tree[rt].mn.mo<upward)
		{
			tree[rt].sum+=tree[rt].mn.cnt*(upward-tree[rt].mn.mo);
			if(tree[rt].mx.mo==tree[rt].mn.mo)  tree[rt].mx.mo=upward;
			if(tree[rt].mx.se==tree[rt].mn.mo)  tree[rt].mx.se=upward;
			tree[rt].downward=max(tree[rt].downward,upward);
			tree[rt].mn.mo=tree[rt].upward=upward;
		}
		if(tree[rt].mx.mo>downward)
		{
			tree[rt].sum-=tree[rt].mx.cnt*(tree[rt].mx.mo-downward);
			if(tree[rt].mn.mo==tree[rt].mx.mo)  tree[rt].mn.mo=downward;
			if(tree[rt].mn.se==tree[rt].mx.mo)  tree[rt].mn.se=downward;
			tree[rt].upward=min(tree[rt].upward,downward);
			tree[rt].mx.mo=tree[rt].downward=downward;
		}
	}
	void pushdown(ll rt)
	{
		pushlazy(lson(rt),tree[rt].add,tree[rt].upward,tree[rt].downward);
		pushlazy(rson(rt),tree[rt].add,tree[rt].upward,tree[rt].downward);
		tree[rt].add=0;  tree[rt].upward=-inf;  tree[rt].downward=inf;
	}
	void update1(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(x<=l&&r<=y)
		{
			pushlazy(rt,val,-inf,inf);
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update1(lson(rt),l,mid,x,y,val);
		if(y>mid)  update1(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	void update2(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(tree[rt].mn.mo>=val)  return;
		if(x<=l&&r<=y&&tree[rt].mn.se>val)
		{
			pushlazy(rt,0,val,inf);
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update2(lson(rt),l,mid,x,y,val);
		if(y>mid)  update2(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	void update3(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(tree[rt].mx.mo<=val)  return;
		if(x<=l&&r<=y&&tree[rt].mx.se<val)
		{
			pushlazy(rt,0,-inf,val);
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update3(lson(rt),l,mid,x,y,val);
		if(y>mid)  update3(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	ll query1(ll rt,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y)  return tree[rt].sum;
		pushdown(rt);
		ll mid=(l+r)/2,ans=0;
		if(x<=mid)  ans+=query1(lson(rt),l,mid,x,y);
		if(y>mid)  ans+=query1(rson(rt),mid+1,r,x,y);
		return ans;
	}
	ll query2(ll rt,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y)  return tree[rt].mx.mo;
		pushdown(rt);
		ll mid=(l+r)/2,ans=-inf;
		if(x<=mid)  ans=max(ans,query2(lson(rt),l,mid,x,y));
		if(y>mid)  ans=max(ans,query2(rson(rt),mid+1,r,x,y));
		return ans;
	}
	ll query3(ll rt,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y)  return tree[rt].mn.mo;
		pushdown(rt);
		ll mid=(l+r)/2,ans=inf;
		if(x<=mid)  ans=min(ans,query3(lson(rt),l,mid,x,y));
		if(y>mid)  ans=min(ans,query3(rson(rt),mid+1,r,x,y));
		return ans;
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,pd,l,r,x,i;
	scanf("%lld",&n);
	for(i=1;i<=n;i++)  scanf("%lld",&a[i]);
	T.build(1,1,n);
	scanf("%lld",&m);
	for(i=1;i<=m;i++)
	{
		scanf("%lld%lld%lld",&pd,&l,&r);
		if(1<=pd&&pd<=3)  scanf("%lld",&x);
		if(pd==1)  T.update1(1,1,n,l,r,x);
		if(pd==2)  T.update2(1,1,n,l,r,x);
		if(pd==3)  T.update3(1,1,n,l,r,x);
		if(pd==4)  printf("%lld\n",T.query1(1,1,n,l,r));
		if(pd==5)  printf("%lld\n",T.query2(1,1,n,l,r));
		if(pd==6)  printf("%lld\n",T.query3(1,1,n,l,r));
	}
	return 0;
}

CF1009F Dominant Indices

树上启发式合并的删除操作并不影响信息合并。

点击查看代码

struct node
{
	int nxt,to;
}e[2000010];
int head[1000010],ans[1000010],cnt=0;
void add(int u,int v)
{
	cnt++;  e[cnt]=(node){head[u],v};  head[u]=cnt;
}
struct DSU_On_Tree
{
	int fa[1000010],siz[1000010],dfn[1000010],out[1000010],pos[1000010],son[1000010],dep[1000010],vis[1000010],maxx=0,opt=0,tot=0;
	void add_rt(int x)
	{
		vis[dep[x]]++;
		if(vis[dep[x]]>maxx||(vis[dep[x]]==maxx&&opt>dep[x]))
		{
			maxx=vis[dep[x]];
			opt=dep[x];
		}
	}
	void del_rt(int x)
	{
		vis[dep[x]]--;
	}
	void add_tree(int x)
	{
		for(int i=dfn[x];i<=out[x];i++)  add_rt(pos[i]);
	}
	void del_tree(int x)
	{
		for(int i=dfn[x];i<=out[x];i++)  del_rt(pos[i]);
	}
	void dfs1(int x,int father)
	{
		tot++;  dfn[x]=tot;  pos[tot]=x;
		siz[x]=1;
		fa[x]=father;
		dep[x]=dep[father]+1;
		for(int i=head[x];i!=0;i=e[i].nxt)
		{
			if(e[i].to!=father)
			{
				dfs1(e[i].to,x);
				siz[x]+=siz[e[i].to];
				son[x]=(siz[e[i].to]>siz[son[x]])?e[i].to:son[x];
			}
		}
		out[x]=tot;
	}
	void dfs2(int x,int flag)
	{
		for(int i=head[x];i!=0;i=e[i].nxt)
		{
			if(e[i].to!=fa[x]&&e[i].to!=son[x])  dfs2(e[i].to,0);
		}
		maxx=opt=0;
		if(son[x]!=0)  dfs2(son[x],1);
		for(int i=head[x];i!=0;i=e[i].nxt)
		{
			if(e[i].to!=fa[x]&&e[i].to!=son[x])  add_tree(e[i].to);
		}
		add_rt(x);
		ans[x]=opt-dep[x];
		if(flag==0)  del_tree(x);
	}
}D;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,u,v,i;
	scanf("%d",&n);
	for(i=1;i<=n-1;i++)
	{
		scanf("%d%d",&u,&v);
		add(u,v);  add(v,u);
	}
	D.dfs1(1,0);  D.dfs2(1,0);
	for(i=1;i<=n;i++)  printf("%d\n",ans[i]);
	return 0;
}

UOJ 169. 【UR #11】元旦老人与数列

将对最小值变成 \(x\) 也看作修改，维护全局信息和最小值当前历史版本最小加法标记即可。

下传标记时特判一下即可。

点击查看代码

const ll inf=0x3f3f3f3f3f3f3f3f;
ll a[500010];
struct SMT
{
	struct node
	{
		ll add,hadd;
		void clear()
		{
			add=hadd=0;
		}
	};
	struct SegmentTree
	{
		ll mn,se,hmn;
		node all,part;
	}tree[2000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void pushup(ll rt)
	{
		tree[rt].hmn=min(tree[lson(rt)].hmn,tree[rson(rt)].hmn);
		tree[rt].mn=min(tree[lson(rt)].mn,tree[rson(rt)].mn);
		if(tree[lson(rt)].mn<tree[rson(rt)].mn)
		{
			tree[rt].se=min(tree[lson(rt)].se,tree[rson(rt)].mn);
		}
		if(tree[lson(rt)].mn==tree[rson(rt)].mn)
		{
			tree[rt].se=min(tree[lson(rt)].se,tree[rson(rt)].se);
		}
		if(tree[lson(rt)].mn>tree[rson(rt)].mn)
		{
			tree[rt].se=min(tree[lson(rt)].mn,tree[rson(rt)].se);
		}
	}
	void build(ll rt,ll l,ll r)
	{
		tree[rt].all.clear();  tree[rt].part.clear();
		if(l==r)
		{
			tree[rt].mn=tree[rt].hmn=a[l];
			tree[rt].se=inf;
			return;
		}
		ll mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	void pushlazy(ll rt,node all,node part)
	{
		tree[rt].hmn=min(tree[rt].hmn,tree[rt].mn+part.hadd);
		tree[rt].mn+=part.add;
		if(tree[rt].se!=inf)  tree[rt].se+=all.add;
		tree[rt].all.hadd=min(tree[rt].all.hadd,tree[rt].all.add+all.hadd);
		tree[rt].all.add+=all.add;
		tree[rt].part.hadd=min(tree[rt].part.hadd,tree[rt].part.add+part.hadd);
		tree[rt].part.add+=part.add;
	}
	void pushdown(ll rt)
	{
		ll mn=min(tree[lson(rt)].mn,tree[rson(rt)].mn);
		pushlazy(lson(rt),tree[rt].all,(tree[lson(rt)].mn==mn)?tree[rt].part:tree[rt].all);
		pushlazy(rson(rt),tree[rt].all,(tree[rson(rt)].mn==mn)?tree[rt].part:tree[rt].all);
		tree[rt].all.clear();  tree[rt].part.clear();
	}
	void update1(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(x<=l&&r<=y)
		{
			pushlazy(rt,(node){val,min(val,0ll)},(node){val,min(val,0ll)});
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update1(lson(rt),l,mid,x,y,val);
		if(y>mid)  update1(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	void update2(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(tree[rt].mn>=val)  return;
		if(x<=l&&r<=y&&tree[rt].se>val)
		{
			pushlazy(rt,(node){0,0},(node){val-tree[rt].mn,0});
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update2(lson(rt),l,mid,x,y,val);
		if(y>mid)  update2(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	ll query1(ll rt,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y)  return tree[rt].mn;
		pushdown(rt);
		ll mid=(l+r)/2,ans=inf;
		if(x<=mid)  ans=min(ans,query1(lson(rt),l,mid,x,y));
		if(y>mid)  ans=min(ans,query1(rson(rt),mid+1,r,x,y));
		return ans;
	}
	ll query2(ll rt,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y)  return tree[rt].hmn;
		pushdown(rt);
		ll mid=(l+r)/2,ans=inf;
		if(x<=mid)  ans=min(ans,query2(lson(rt),l,mid,x,y));
		if(y>mid)  ans=min(ans,query2(rson(rt),mid+1,r,x,y));
		return ans;
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,pd,l,r,x,i;
	scanf("%lld%lld",&n,&m);
	for(i=1;i<=n;i++)  scanf("%lld",&a[i]);
	T.build(1,1,n);
	for(i=1;i<=m;i++)
	{
		scanf("%lld%lld%lld",&pd,&l,&r);
		if(pd==1||pd==2)  scanf("%lld",&x);
		if(pd==1)  T.update1(1,1,n,l,r,x);
		if(pd==2)  T.update2(1,1,n,l,r,x);
		if(pd==3)  printf("%lld\n",T.query1(1,1,n,l,r));
		if(pd==4)  printf("%lld\n",T.query2(1,1,n,l,r));
	}
	return 0;
}

UOJ 164. 【清华集训2015】V

将每个操作转化成 \(y \gets \max(y+a,b)\) 的形式，分别有 \(\begin{cases} a_{1}=x,b_{1}=0 \\ a_{2}=-x,b_{2}=0 \\ a_{3}=-\infty,b_{3}=x \end{cases}\) 。不妨把原序列也看作操作 \(3\) 。
对于操作 \(4\) 有 \(\max(\max(y+a,b)+c,d)=\max(y+a+c,\max(b+c,d))\) ，直接合并函数即可。

对于操作 \(5\) ，函数复合只可能有如下两种情况。只需要记录 \(a,b\) 的最大值即可。

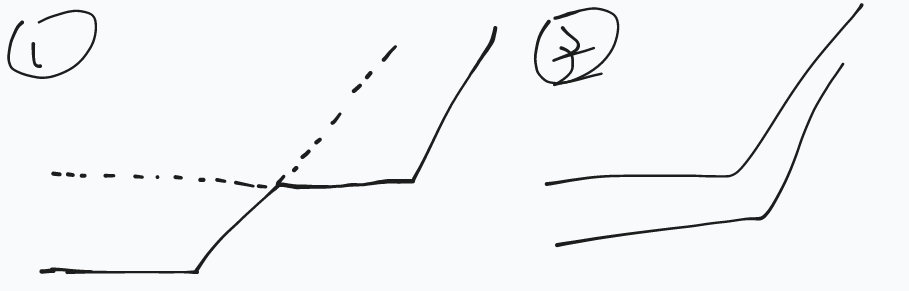
点击查看代码

const ll inf=0x3f3f3f3f3f3f3f3f;
ll a[500010];
struct SMT
{
	struct SegmentTree
	{
		pair<ll,ll>add,hadd;
	}tree[2000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)	
	void build(ll rt,ll l,ll r)
	{
		if(l==r)
		{
			tree[rt].add=tree[rt].hadd=make_pair(a[l],0);
			return;
		}
		ll mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
	}
	void pushlazy(ll rt,pair<ll,ll>add,pair<ll,ll>hadd)
	{
		tree[rt].hadd.first=max(tree[rt].hadd.first,tree[rt].add.first+hadd.first);  
		tree[rt].hadd.second=max({tree[rt].hadd.second,hadd.second,
								tree[rt].add.second+hadd.first});
		tree[rt].add.first=max(tree[rt].add.first+add.first,-inf); 
		tree[rt].add.second=max(tree[rt].add.second+add.first,add.second);
	}
	void pushdown(ll rt)
	{
		pushlazy(lson(rt),tree[rt].add,tree[rt].hadd);
		pushlazy(rson(rt),tree[rt].add,tree[rt].hadd);
		tree[rt].add=tree[rt].hadd=make_pair(0,0);
	}
	void update(ll rt,ll l,ll r,ll x,ll y,pair<ll,ll>add,pair<ll,ll>hadd)
	{
		if(x<=l&&r<=y)
		{
			pushlazy(rt,add,hadd);
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,add,hadd);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,add,hadd);
	}
	ll query(ll rt,ll l,ll r,ll pos,ll op)
	{
		if(l==r)  return (op==4)?max(tree[rt].add.first,tree[rt].add.second):
								max(tree[rt].hadd.first,tree[rt].hadd.second);
		pushdown(rt);
		ll mid=(l+r)/2;
		if(pos<=mid)  return query(lson(rt),l,mid,pos,op);
		else  return query(rson(rt),mid+1,r,pos,op);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,pd,l,r,x,i;
	scanf("%lld%lld",&n,&m);
	for(i=1;i<=n;i++)  scanf("%lld",&a[i]);
	T.build(1,1,n);
	for(i=1;i<=m;i++)
	{
		scanf("%lld%lld",&pd,&l);
		if(pd==1||pd==2||pd==3)  scanf("%lld%lld",&r,&x);
		if(pd==1)  T.update(1,1,n,l,r,make_pair(x,0),make_pair(x,0));
		if(pd==2)  T.update(1,1,n,l,r,make_pair(-x,0),make_pair(-x,0));
		if(pd==3)  T.update(1,1,n,l,r,make_pair(-inf,x),make_pair(-inf,x));
		if(pd==4||pd==5)  printf("%lld\n",T.query(1,1,n,l,pd));
	}
	return 0;
}

luogu P6242 【模板】线段树 3（区间最值操作、区间历史最值）

在 UOJ 169. 【UR #11】元旦老人与数列的基础上加上维护区间和即可。

点击查看代码

ll a[500010];
struct SMT
{
	struct node
	{
		ll add,hadd;
		void clear()
		{
			add=hadd=0;
		}
	};
	struct SegmentTree
	{
		ll sum,len,hmx,mx,se,cnt;
		node all,part;
	}tree[2000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void pushup(ll rt)
	{
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum;
		tree[rt].hmx=max(tree[lson(rt)].hmx,tree[rson(rt)].hmx);
		tree[rt].mx=max(tree[lson(rt)].mx,tree[rson(rt)].mx);
		if(tree[lson(rt)].mx>tree[rson(rt)].mx)
		{
			tree[rt].se=max(tree[lson(rt)].se,tree[rson(rt)].mx);
			tree[rt].cnt=tree[lson(rt)].cnt;
		}
		if(tree[lson(rt)].mx==tree[rson(rt)].mx)
		{
			tree[rt].se=max(tree[lson(rt)].se,tree[rson(rt)].se);
			tree[rt].cnt=tree[lson(rt)].cnt+tree[rson(rt)].cnt;
		}
		if(tree[lson(rt)].mx<tree[rson(rt)].mx)
		{
			tree[rt].se=max(tree[lson(rt)].mx,tree[rson(rt)].se);
			tree[rt].cnt=tree[rson(rt)].cnt;
		}
	}
	void build(ll rt,ll l,ll r)
	{
		tree[rt].all.clear();  tree[rt].part.clear();
		tree[rt].len=r-l+1;
		if(l==r)
		{
			tree[rt].mx=tree[rt].sum=tree[rt].hmx=a[l];
			tree[rt].se=-1;  tree[rt].cnt=1;
			return;
		}
		ll mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	void pushlazy(ll rt,node all,node part)
	{
		tree[rt].sum+=(tree[rt].len-tree[rt].cnt)*all.add+tree[rt].cnt*part.add;
		tree[rt].hmx=max(tree[rt].hmx,tree[rt].mx+part.hadd);
		tree[rt].mx+=part.add;
		if(tree[rt].se!=-1)  tree[rt].se+=all.add;
		tree[rt].all.hadd=max(tree[rt].all.hadd,tree[rt].all.add+all.hadd);
		tree[rt].all.add+=all.add;
		tree[rt].part.hadd=max(tree[rt].part.hadd,tree[rt].part.add+part.hadd);
		tree[rt].part.add+=part.add;
	}
	void pushdown(ll rt)
	{
		ll mx=max(tree[lson(rt)].mx,tree[rson(rt)].mx);
		pushlazy(lson(rt),tree[rt].all,(tree[lson(rt)].mx==mx)?tree[rt].part:tree[rt].all);
		pushlazy(rson(rt),tree[rt].all,(tree[rson(rt)].mx==mx)?tree[rt].part:tree[rt].all);
		tree[rt].all.clear();  tree[rt].part.clear(); 
	}
	void update1(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(x<=l&&r<=y)
		{
			pushlazy(rt,(node){val,max(val,0ll)},(node){val,max(val,0ll)});
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update1(lson(rt),l,mid,x,y,val);
		if(y>mid)  update1(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	void update2(ll rt,ll l,ll r,ll x,ll y,ll val)
	{
		if(tree[rt].mx<=val)  return;
		if(x<=l&&r<=y&&tree[rt].se<val)
		{
			pushlazy(rt,(node){0,0},(node){val-tree[rt].mx,0});
			return;
		}
		pushdown(rt);
		ll mid=(l+r)/2;
		if(x<=mid)  update2(lson(rt),l,mid,x,y,val);
		if(y>mid)  update2(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	ll query1(ll rt,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y)  return tree[rt].sum;
		pushdown(rt);
		ll mid=(l+r)/2,ans=0;
		if(x<=mid)  ans+=query1(lson(rt),l,mid,x,y);
		if(y>mid)  ans+=query1(rson(rt),mid+1,r,x,y);
		return ans;
	}
	ll query2(ll rt,ll l,ll r,ll x,ll y,ll op)
	{
		if(x<=l&&r<=y)  return (op==4)?tree[rt].mx:tree[rt].hmx;
		pushdown(rt);
		ll mid=(l+r)/2,ans=-0x3f3f3f3f3f3f3f3f;
		if(x<=mid)  ans=max(ans,query2(lson(rt),l,mid,x,y,op));
		if(y>mid)  ans=max(ans,query2(rson(rt),mid+1,r,x,y,op));
		return ans;
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,pd,l,r,x,i;
	scanf("%lld%lld",&n,&m);
	for(i=1;i<=n;i++)  scanf("%lld",&a[i]);
	T.build(1,1,n);
	for(i=1;i<=m;i++)
	{
		scanf("%lld%lld%lld",&pd,&l,&r);
		if(pd==1||pd==2)  scanf("%lld",&x);
		if(pd==1)  T.update1(1,1,n,l,r,x);
		if(pd==2)  T.update2(1,1,n,l,r,x);
		if(pd==3)  printf("%lld\n",T.query1(1,1,n,l,r));
		if(pd==4)  printf("%lld\n",T.query2(1,1,n,l,r,pd));
		if(pd==5)  printf("%lld\n",T.query2(1,1,n,l,r,pd));
	}
	return 0;
}

3.25

闲话

做题纪要

luogu P11833 [省选联考 2025] 推箱子

因为题目要求第 \(i\) 个箱子在时刻 \(t_{i}\) 以及之后的所有时刻都处于数轴的 \(b_{i}\) 处，所以不会出现 [ABC371F] Takahashi in Narrow Road 样例中的情况，简化了处理方式。
观察到每时每刻箱子位置的相对大小关系不会发生改变，贪心地考虑优先满足 \(t_{i}\) 较小的限制。

将箱子的整体移动看做区间赋值等差数列即可，令 \(a_{i} \gets a_{i}-i\) 后珂朵莉树维护。

点击查看代码

struct node
{
	ll t,st,ed,id;
}a[200010];
bool cmp(node a,node b)
{
	return a.t<b.t;
}
struct ODT
{
	struct node
	{
		ll l,r;
		mutable ll col;
		bool operator < (const node &another) const
		{
			return l<another.l;
		}
	};
	set<node>s;
	void init(ll n)
	{
		s.clear();
		for(ll i=1;i<=n;i++)  s.insert((node){i,i,a[i].st});
	}
	set<node>::iterator split1(ll pos)
	{
		set<node>::iterator it=--s.upper_bound((node){pos,-1,-1});
		if(it->l!=pos)
		{	
			ll l=it->l,r=it->r,col=it->col;
			s.erase(it);   s.insert((node){l,pos-1,col});
			it=s.insert((node){pos,r,col}).first;
		}
		return it;
	}
	set<node>::iterator split2(ll pos)
	{
		set<node>::iterator it=--s.upper_bound((node){pos,-1,-1});
		if(it->r!=pos)
		{	
			ll l=it->l,r=it->r,col=it->col;
			s.erase(it);   s.insert((node){pos+1,r,col});
			it=s.insert((node){l,pos,col}).first;
		}
		return it;
	}
	ll assign1(ll l,ll col)
	{
		set<node>::iterator itl=split1(l),itr;
		ll ans=0,r=l-1;
		for(set<node>::iterator it=itl;it!=s.end()&&it->col<col;it++)
		{
			ans+=(it->r-it->l+1)*(col-it->col);
			itr=it;  r=it->r;
		}
		if(l<=r)
		{
			s.erase(itl,next(itr));  s.insert((node){l,r,col});
		}
		return ans;
	}
	ll assign2(ll r,ll col)
	{
		set<node>::iterator itr=split2(r),itl;
		ll ans=0,l=r+1;	
		for(set<node>::iterator it=itr;it->col>col;it--)
		{
			ans+=(it->r-it->l+1)*(it->col-col);
			itl=it;  l=it->l;
			if(it==s.begin())  break;
		}
		if(l<=r)
		{
			s.erase(itl,next(itr));  s.insert((node){l,r,col});
		}
		return ans;
	}
}O;
int main()
{
#define Isaac 
#ifdef Isaac
	freopen("move.in","r",stdin);
	freopen("move.out","w",stdout);
#endif
	ll c,t,n,flag,sum,i;
	scanf("%lld%lld",&c,&t);
	for(;t>=1;t--)
	{
		scanf("%lld",&n);  flag=1;  sum=0;
		for(i=1;i<=n;i++)  
		{
			scanf("%lld%lld%lld",&a[i].st,&a[i].ed,&a[i].t);
			a[i].st-=i;  a[i].ed-=i;  a[i].id=i;
		}
		O.init(n);  sort(a+1,a+1+n,cmp);  
		for(i=1;i<=n&&flag==1;i++)  
		{
			sum+=(a[i].st<a[i].ed)?O.assign1(a[i].id,a[i].ed):O.assign2(a[i].id,a[i].ed);
			if(sum>a[i].t)  flag=0;
		}
		if(flag==1)  printf("Yes\n");
		else  printf("No\n");
	}
	return 0;
}

3.26

闲话

做题纪要

luogu P2468 [SDOI2010] 粟粟的书架

数据点分治。观察到值域较小所以直接二分即可。

点击查看代码

const int inf=1000;
int a[210][210],b[500010],sum[210][210][1010],num[210][210][1010];
struct PDS_SMT
{
	int root[500010],rt_sum;
	struct SegmentTree
	{
		int ls,rs,siz,sum;
	}tree[500010<<5];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt()
	{
		rt_sum++;
		lson(rt_sum)=rson(rt_sum)=tree[rt_sum].siz=tree[rt_sum].sum=0;
		return rt_sum;
	}
	void update(int pre,int &rt,int l,int r,int pos)
	{
		rt=build_rt();  tree[rt]=tree[pre];
		tree[rt].siz++;  tree[rt].sum+=pos;
		if(l==r)  return;
		int mid=(l+r)/2;	
		if(pos<=mid)  update(lson(pre),lson(rt),l,mid,pos);
		else  update(rson(pre),rson(rt),mid+1,r,pos);
	}
	int query(int rt1,int rt2,int l,int r,int val)
	{
		if(tree[rt2].sum-tree[rt1].sum<val)  return -1;
		if(l==r)  return ceil(1.0*val/l);
		int mid=(l+r)/2,sum=tree[rson(rt2)].sum-tree[rson(rt1)].sum;
		if(sum>=val)  return query(rson(rt1),rson(rt2),mid+1,r,val);
		return tree[rson(rt2)].siz-tree[rson(rt1)].siz+query(lson(rt1),lson(rt2),l,mid,val-sum);
	}
}T;
int query1(int x1,int y1,int x2,int y2,int k)
{
	return sum[x2][y2][k]-sum[x1-1][y2][k]-sum[x2][y1-1][k]+sum[x1-1][y1-1][k];
}
int query2(int x1,int y1,int x2,int y2,int k)
{
	return num[x2][y2][k]-num[x1-1][y2][k]-num[x2][y1-1][k]+num[x1-1][y1-1][k];
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,q,x1,y1,x2,y2,h,l,r,ans,mid,i,j,k;
	cin>>n>>m>>q;
	if(n==1)
	{
		for(i=1;i<=m;i++) 
		{
			cin>>b[i];  T.update(T.root[i-1],T.root[i],1,inf,b[i]);
		}
		for(i=1;i<=q;i++)
		{
			cin>>x1>>y1>>x2>>y2>>h;
			ans=T.query(T.root[y1-1],T.root[y2],1,inf,h);
			if(ans!=-1)  cout<<ans<<endl;
			else  cout<<"Poor QLW"<<endl;
		}
	}
	else
	{
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=m;j++)
			{
				cin>>a[i][j];
				for(k=1;k<=inf;k++)
				{
					sum[i][j][k]=sum[i-1][j][k]+sum[i][j-1][k]-sum[i-1][j-1][k]+(a[i][j]>=k)*a[i][j];
					num[i][j][k]=num[i-1][j][k]+num[i][j-1][k]-num[i-1][j-1][k]+(a[i][j]>=k);
				}
			}
		}
		for(i=1;i<=q;i++)
		{
			cin>>x1>>y1>>x2>>y2>>h;
			l=1;  r=inf;  ans=-1;
			while(l<=r)
			{
				mid=(l+r)/2;
				if(query1(x1,y1,x2,y2,mid)>=h)
				{
					ans=mid;
					l=mid+1;
				}
				else  r=mid-1;
			}
			if(ans!=-1)  cout<<query2(x1,y1,x2,y2,ans+1)+ceil(1.0*(h-query1(x1,y1,x2,y2,ans+1))/ans)<<endl;
			else  cout<<"Poor QLW"<<endl;
		}
	}
	return 0;
}

CF1140F Extending Set of Points

拓展是一个形如可达性复制的形式。
将 \((x,y)\) 看做二分图上左部点 \(x\) 向右部点 \(y\) 连的边，最后每个连通块内部会被扩展成一张完全二分图，其贡献为左右两部点数量的乘积。

线段树分治即可。

点击查看代码

ll u[300010],v[300010],ans[300010];
map<pair<ll,ll>,ll>f;
map<pair<ll,ll>,ll>::iterator it;
struct quality
{
	ll fa,id;
	pair<ll,ll>siz;
};
struct DSU
{
	ll fa[600010];
	pair<ll,ll>siz[600010];
	void init(ll n)
	{
		for(ll i=1;i<=n;i++)
		{
			fa[i]=i;
			siz[i]=(i<=n/2)?make_pair(1,0):make_pair(0,1);
		}
	}
	ll find(ll x)
	{
		return fa[x]==x?x:find(fa[x]);
	}
	void merge(ll x,ll y,stack<quality>&s,ll &sum)
	{
		x=find(x);  y=find(y);
		if(x!=y)
		{
			if(siz[x]>siz[y])  swap(x,y);
			s.push((quality){fa[x],x,siz[x]});
			s.push((quality){fa[y],y,siz[y]});
			sum-=siz[x].first*siz[x].second+siz[y].first*siz[y].second; 
			fa[x]=y;  siz[y].first+=siz[x].first;  siz[y].second+=siz[x].second;
			sum+=siz[y].first*siz[y].second;
		}
	}
	void split(stack<quality>&s)
	{
		while(s.empty()==0)
		{
			fa[s.top().id]=s.top().fa;
			siz[s.top().id]=s.top().siz;
			s.pop();
		}
	}
}D;
struct SMT
{
	vector<ll>tree[1200010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void update(ll rt,ll l,ll r,ll x,ll y,ll id)
	{
		if(x<=l&&r<=y)
		{
			tree[rt].push_back(id);
			return;
		}
		ll mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,id);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,id);
	}
	void solve(ll rt,ll l,ll r,ll sum)
	{
		stack<quality>s;
		for(ll i=0;i<tree[rt].size();i++)  D.merge(u[tree[rt][i]],v[tree[rt][i]],s,sum);
		if(l==r)  ans[l]=sum;
		else
		{
			ll mid=(l+r)/2;
			solve(lson(rt),l,mid,sum);  solve(rson(rt),mid+1,r,sum);
		}
		D.split(s);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int q,i;
	cin>>q;  D.init(600000);
	for(i=1;i<=q;i++)
	{
		cin>>u[i]>>v[i];  v[i]+=300000;
		if(f.find(make_pair(u[i],v[i]))==f.end())  f[make_pair(u[i],v[i])]=i;
		else  
		{
			T.update(1,1,q,f[make_pair(u[i],v[i])],i-1,i);
			f.erase(make_pair(u[i],v[i]));
		}
	}
	for(it=f.begin();it!=f.end();it++)  T.update(1,1,q,it->second,q,it->second);
	T.solve(1,1,q,0);
	for(i=1;i<=q;i++)  cout<<ans[i]<<" ";
	return 0;
}

3.27

闲话

做题纪要

AT_agc006_f [AGC006F] Blackout

若能建出三分图，贡献则为相邻两部点数量乘积之和；否则为连通块大小的平方（出现过三种颜色）或原边数（仅有两种颜色）。

点击查看代码

ll vis[100010],col[100010],flag,siz,cnt[3];
vector<pair<ll,ll> >e[100010];
void add(ll u,ll v,ll w)
{
	e[u].push_back(make_pair(v,w));
}
void dfs(ll x)
{
	vis[x]=1;  cnt[col[x]]++;
	siz+=e[x].size();
	for(ll i=0;i<e[x].size();i++)
	{
		if(vis[e[x][i].first]==0)
		{
			col[e[x][i].first]=(col[x]+e[x][i].second)%3;
			dfs(e[x][i].first);
		}
		else  flag|=(col[e[x][i].first]!=(col[x]+e[x][i].second)%3);
	}
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,u,v,ans=0,i;
	cin>>n>>m;
	for(i=1;i<=m;i++)
	{
		cin>>u>>v;
		add(u,v,1);  add(v,u,2);
	}
	for(i=1;i<=n;i++)
	{
		if(vis[i]==0)
		{
			cnt[0]=cnt[1]=cnt[2]=flag=siz=0;
			dfs(i);
			if(flag==1)  ans+=(cnt[0]+cnt[1]+cnt[2])*(cnt[0]+cnt[1]+cnt[2]);
			else  if(cnt[0]==0||cnt[1]==0||cnt[2]==0)  ans+=siz/2;
			else  ans+=cnt[0]*cnt[1]+cnt[0]*cnt[2]+cnt[1]*cnt[2];
		}
	}
	cout<<ans<<endl;
	return 0;
}

3.28

闲话

到机房后因他们在补 \(whk\) 遂又搬到 \(510\) 了。
下午信息改成公自了，白从柜子里把信息课本找出来。所以有两节公自，班主任以为我们这两节就可以把作业写完了。
学校还组织了脊柱侧弯的检查，貌似比较严重的每人给发了张单说建议去复查。
临吃晚饭时班长开完会回来说周五晚上和周日晚上应该是安排在教室上自习写作业；今天晚新闻的时候练习远足之歌；远足的时候禁止带零食，两人一排，不允许打闹，具体要求到时候再说，不参加者记入德育量化总分；下周一早上有升旗；因本次放假回家人数较少，所以安排在教室上自习，体活时间为明天上午第 \(5\) 节。
班主任来了之后说奥赛班体活时间不变，仍为明天下午第 \(10\) 节；明天早上 \(7:15\) 到各奥赛教室；除信奥外其他奥赛要去打扫滏阳楼。

做题纪要

CF576E Painting Edges

因修改只在合法情况才进行修改，所以只需要考虑只保留修改后的颜色是不是二分图。

将操作划分成若干段视作其影响即可。

点击查看代码

int u[500010],v[500010],w[500010],x[500010],y[500010],last[500010],n,m,k,q;
struct quality
{
	int fa,siz,col,id;
};
struct DSU
{
	int fa[60][1000010],siz[60][1000010];
	int find(int x,int col)
	{
		return fa[col][x]==x?x:find(fa[col][x],col);
	}
	void init(int n,int k)
	{
		for(int j=1;j<=k;j++)
		{
			for(int i=1;i<=n;i++)
			{
				fa[j][i]=i;  siz[j][i]=1;
			}
		}
	}
	void merge(int x,int y,int col,stack<quality>&s)
	{
		x=find(x,col);  y=find(y,col);
		if(x!=y)
		{
			s.push((quality){fa[col][x],siz[col][x],col,x});
			s.push((quality){fa[col][y],siz[col][y],col,y});
			if(siz[col][x]>siz[col][y])  swap(x,y);
			fa[col][x]=y;  siz[col][y]+=siz[col][x];
		}
	}
	void split(stack<quality>&s)
	{
		while(s.empty()==0)
		{
			fa[s.top().col][s.top().id]=s.top().fa;
			siz[s.top().col][s.top().id]=s.top().siz;
			s.pop();
		}
	}
}D;
struct SMT
{
	vector<int>tree[2000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void update(int rt,int l,int r,int x,int y,int id)
	{
		if(x<=l&&r<=y)
		{
			tree[rt].push_back(id);
			return;
		}
		int mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,id);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,id);
	}
	void solve(int rt,int l,int r)
	{
		stack<quality>s;
		int mid=(l+r)/2,pos;
		for(int i=0;i<tree[rt].size();i++)
		{
			pos=x[tree[rt][i]];
			if(w[x[tree[rt][i]]]!=0)
			{
				D.merge(u[pos],v[pos]+n,w[pos],s);
				D.merge(v[pos],u[pos]+n,w[pos],s);
			}
		}
		if(l==r)
		{
			if(D.find(u[x[l]],y[l])!=D.find(v[x[l]],y[l]))
			{
				printf("YES\n");
				w[x[l]]=y[l];
			}
			else  printf("NO\n");
		}
		else
		{
			solve(lson(rt),l,mid);  solve(rson(rt),mid+1,r);
		}
		D.split(s);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	scanf("%d%d%d%d",&n,&m,&k,&q);  D.init(2*n,k);
	for(int i=1;i<=m;i++)  
	{
		scanf("%d%d",&u[i],&v[i]);
		last[i]=q+1;
	}
	for(int i=1;i<=q;i++)  scanf("%d%d",&x[i],&y[i]);
	for(int i=q;i>=1;i--)
	{
		if(i+1<=last[x[i]]-1)  T.update(1,1,q,i+1,last[x[i]]-1,i);
		last[x[i]]=i;
	}
	T.solve(1,1,q);
	return 0;
}

luogu P11961 [GESP202503 五级] 原根判断

原根判断定理。

暴力分解质因数可以接受。

点击查看代码

ll phi;
vector<ll>result;
void divide(ll n)
{
	result.clear();
	for(ll i=2;i*i<=n;i++)
	{
		if(n%i==0)
		{
			result.push_back(i);
			while(n%i==0)  n/=i;
		}
	}
	if(n>1)  result.push_back(n);
}
ll qpow(ll a,ll b,ll p)
{
	ll ans=1;
	while(b)
	{
		if(b&1)  ans=ans*a%p;
		b>>=1;
		a=a*a%p;
	}
	return ans;
}
bool check(ll x,ll p)
{
	if(qpow(x,phi,p)!=1)  return false;
	for(ll i=0;i<result.size();i++)
	{
		if(qpow(x,phi/result[i],p)==1)  return false;
	}
	return true;
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif		
	ll t,x,p,i;
	cin>>t;
	for(i=1;i<=t;i++)
	{
		cin>>x>>p;  phi=p-1;  divide(phi);
		cout<<(check(x,p)==true?"Yes":"No")<<endl;
	}
	return 0;
}

luogu P4198 楼房重建

令 \(s_{i}=\frac{h_{i}}{i}\) 则等价于查询全局有多少个严格前缀最大值。

兔队线段树。

对于线段树上某个节点 \([l,r]\) ，分别维护 \([l,r]\) 内 \(s_{i}\) 的最大值和仅考虑左区间对右区间的贡献时右区间的答案（叶子节点时后者没有定义）。
前者是容易维护的；后者则需要引入另外一个函数 ask(rt,l,r,val) 返回 \([l,r]\) 内考虑了前缀最大值 \(val\) 后的答案，本质上是一个类似线段树上二分的过程。
- 另外一种写法是维护仅考虑左区间对右区间的贡献时该区间的总答案，此时就需要其满足一定的可加性，具有一定的局限性。
时间复杂度为 \(O(m \log^{2} n)\) 。

点击查看代码

ll a[100010];
bool cmp(ll x,ll y)
{
	return (y==0)?a[x]:a[x]*y>a[y]*x;
}
ll sx_max(ll x,ll y)
{
	return cmp(x,y)==true?x:y;
}
struct SMT
{
	struct SegmentTree
	{
		ll pos,ans;
	}tree[400010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	ll ask(ll rt,ll l,ll r,ll val)
	{
		if(l==r)  return cmp(l,val);
		ll mid=(l+r)/2;
		if(cmp(tree[lson(rt)].pos,val)==true)  return ask(lson(rt),l,mid,val)+tree[rt].ans;
		return ask(rson(rt),mid+1,r,val);
	}
	void pushup(ll rt,ll l,ll r)
	{
		ll mid=(l+r)/2;
		tree[rt].pos=sx_max(tree[lson(rt)].pos,tree[rson(rt)].pos);
		tree[rt].ans=ask(rson(rt),mid+1,r,tree[lson(rt)].pos);
	}
	void build(ll rt,ll l,ll r)
	{
		tree[rt].pos=l;
		if(l==r)  return;
		ll mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
	}
	void update(ll rt,ll l,ll r,ll pos,ll val)
	{
		if(l==r)
		{
			a[pos]=val;
			return;
		}
		ll mid=(l+r)/2;
		if(pos<=mid)  update(lson(rt),l,mid,pos,val);
		else  update(rson(rt),mid+1,r,pos,val);
		pushup(rt,l,r);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,x,y,i;
	cin>>n>>m;  T.build(1,1,n);
	for(i=1;i<=m;i++)
	{
		cin>>x>>y;  T.update(1,1,n,x,y);
		cout<<T.ask(1,1,n,0)<<endl;
	}
	return 0;
}

3.29

闲话

晚上 \(field\) 说了下学考前课表调整的情况，每周少的六节奥赛课改成政史地各两节。

做题纪要

UOJ 515. 【UR #19】前进四

以时间为下标从右往左进行扫描线，每次修改若能进行变化（由大的变成小的）则贡献加一，吉司机线段树维护即可。

点击查看代码

struct node
{
	int id,val;
	pair<int,int>tim;
}c[2000010],q[1000010];
int a[1000010],ans[1000010];
bool cmp(node a,node b)
{
	if(a.id!=b.id)  return a.id>b.id;
	return a.tim>b.tim;
}
struct SMT
{
	struct SegmentTree
	{
		int mx,se,lazy;
	}tree[4000010];
	#define lson(rt) (rt<<1)
	#define rson(rt) (rt<<1|1)
	void pushup(int rt)
	{
		tree[rt].mx=max(tree[lson(rt)].mx,tree[rson(rt)].mx);
		if(tree[lson(rt)].mx>tree[rson(rt)].mx)  tree[rt].se=max(tree[lson(rt)].se,tree[rson(rt)].mx);
		if(tree[lson(rt)].mx==tree[rson(rt)].mx)  tree[rt].se=max(tree[lson(rt)].se,tree[rson(rt)].se);
		if(tree[lson(rt)].mx<tree[rson(rt)].mx)  tree[rt].se=max(tree[lson(rt)].mx,tree[rson(rt)].se);
	}
	void build(int rt,int l,int r)
	{
		tree[rt].mx=0x3f3f3f3f;  tree[rt].se=-1;
		if(l==r)  return;
		int mid=(l+r)/2;
		build(lson(rt),l,mid);  build(rson(rt),mid+1,r);
	}
	void pushlazy(int rt,int val,int lazy)
	{
		if(tree[rt].mx<=val)  return;
		tree[rt].mx=val;
		tree[rt].lazy+=lazy;
	}
	void pushdown(int rt)
	{
		pushlazy(lson(rt),tree[rt].mx,tree[rt].lazy);
		pushlazy(rson(rt),tree[rt].mx,tree[rt].lazy);
		tree[rt].lazy=0;
	}
	void update(int rt,int l,int r,int x,int y,int val)
	{
		if(tree[rt].mx<=val)  return;
		if(x<=l&&r<=y&&tree[rt].se<val)
		{
			pushlazy(rt,val,1);
			return;
		}
		pushdown(rt);
		int mid=(l+r)/2;
		if(x<=mid)  update(lson(rt),l,mid,x,y,val);
		if(y>mid)  update(rson(rt),mid+1,r,x,y,val);
		pushup(rt);
	}
	int query(int rt,int l,int r,int pos)
	{
		if(l==r)  return tree[rt].lazy;
		pushdown(rt);
		int mid=(l+r)/2;
		if(pos<=mid)  return query(lson(rt),l,mid,pos);
		else  return query(rson(rt),mid+1,r,pos);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,last,pd,c_cnt=0,q_cnt=0,i,j,k;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)  
	{
		scanf("%d",&a[i]);
		c_cnt++;  c[c_cnt]=(node){i,a[i],make_pair(0,i)};
	}
	for(i=1;i<=m;i++)
	{
		scanf("%d",&pd);
		if(pd==1)
		{
			c_cnt++;  scanf("%d%d",&c[c_cnt].id,&c[c_cnt].val);
			c[c_cnt].tim=make_pair(q_cnt+1,i);
		}
		else  
		{
			q_cnt++;  scanf("%d",&q[q_cnt].id);
			q[q_cnt].tim=make_pair(q_cnt,i);
		}
	}
	sort(c+1,c+1+c_cnt,cmp);  sort(q+1,q+1+q_cnt,cmp);
	T.build(1,0,q_cnt);
	for(i=n,j=1,k=1;i>=1;i--)
	{
		for(last=q_cnt;j<=c_cnt&&c[j].id==i;j++)
		{	
			if(c[j].tim.first<=last)
			{
				T.update(1,0,q_cnt,c[j].tim.first,last,c[j].val);
				last=c[j].tim.first-1;
			}
		}
		for(;k<=q_cnt&&q[k].id==i;k++)  ans[q[k].tim.first]=T.query(1,0,q_cnt,q[k].tim.first);
	}
	for(i=1;i<=q_cnt;i++)  printf("%d\n",ans[i]);
	return 0;
}

luogu P11822 [湖北省选模拟 2025] 团队分组 / divide

题面说的很唬人，直接从后往前挑选区间即可。
暴力寻找区间的时间复杂度为 \(O(n^{2})/O(n^{2} \log n)\) ，加之以经典结论可以获得 \(90pts\) luogu 205003209 。
维护 \(f_{r,len}\) 表示 \([r-len+1,r]\) 内字典序最大时的权值和（除去了 \(r+1\) ）的贡献， \(g_{r,len}\) 表示 \([r-len+1,r]\) 内字典序最大时的段数。

观察到长度 \(\ge \sqrt{n}\) 的区间至多有 \(\sqrt{n}\) 种，暴力跳即可；否则进行记忆化。

点击查看代码

ll a[100010],sum[100010],klen=200;
pair<ll,ll>f[100010][210];
pair<ll,ll> solve(ll r,ll limit)
{
	if(sum[r]<=limit)  return make_pair(0,0);
	ll pos=lower_bound(sum+1,sum+1+r,sum[r]-limit)-sum,len=r-pos+1;
	if(len<=klen&&f[r][len].first!=-1)  return f[r][len];
	pair<ll,ll>tmp=solve(pos-1,sum[r]-sum[pos-1]);
	tmp=make_pair(tmp.first+(tmp.second+1)*pos,tmp.second+1);
	return len<=klen?f[r][len]=tmp:tmp;
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("divide.in","r",stdin);
	freopen("divide.out","w",stdout);
#endif
	ll n,i;
	scanf("%lld",&n);  memset(f,-1,sizeof(f));
	for(i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);  sum[i]=sum[i-1]+a[i];
		pair<ll,ll>tmp=solve(i,0);
		printf("%lld ",tmp.first+(tmp.second+1)*(i+1));
	}
	return 0;
}

luogu P4148 简单题

\(KD-Tree\)

\(KD-Tree\) 能够快速处理 \(k\) 维空间信息的数据结构，在遇到的问题中一般有 \(k=2\) 。
\(KD-Tree\) 是一棵二叉搜索树，每个节点对应 \(k\) 维空间上的一个点，子树内的点都在一个 \(k\) 维的超长方体内，且这个超长方体内的所有节点也都在这棵子树内。
假设我们已经知道了 \(k\) 维空间上的 \(n\) 个点要构建一棵 \(KD-Tree\) 时，需进行选择一个维度和一个切割点的操作。为保证其复杂度，需要进行优化以至树高为 \(\log n+O(1)\) ，时间复杂度为 \(O(n \log n)\) 。
- 轮流选择 \(k\) 个维度，保证任意连续 \(k\) 层里每个维度都被切割到。
- 切割点选择这一维度的中位数，可以使用 nth_element 简化代码书写。
而对高维空间进行操作时，记录每个结点子树内每一维度上的坐标的最大值和最小值。如果当前子树对应的矩形与操作矩形没有交点，则不继续搜索其子树；如果当前子树对应的矩形完全包含在操作矩形内，则对当前子树进行操作；否则，判断当前点是否在操作矩形内，更新信息并递归在左右子树中继续操作。查询的时间复杂度为 \(O(n^{1-\frac{1}{k}})\) 。
插入和删除操作影响了 \(KD-Tree\) 的平衡性，而 \(KD-Tree\) 无法进行旋转或随机优先级。常见的两种维护方法是根号重构和二进制分组。
- 根号重构
  - 每进行 \(B\) 次插入/删除操作进行一次重构。
  - 单次重构的复杂度均摊为 \(O(\frac{n \log n}{B})\) ，单次查询为 \(O(B+n^{1-\frac{1}{k}})\) 。在 \(n,m\) 同阶时取 \(B=\sqrt{n \log n}\) 最优，此时重构的复杂度均摊为 \(O(\sqrt{n \log n})\) ，单次查询为 \(O(\sqrt{n \log n}+n^{1-\frac{1}{k}})\) 。
- 二进制分组
  - 维护若干棵大小为 \(2\) 的整数次幂的 \(KD-Tree\) ，满足满足这些树的大小之和为 \(n\) 。
  - 插入的时候，新增一棵大小为 \(1\) 的 \(kD-Tree\)，然后不断将相同大小的树合并并最后一起重构。
  - 修改的总复杂度均摊为 \(O(n \log^{2} n)\) ，单次查询为 \(O(n^{1-\frac{1}{k}})\) 。
常见的写法有平衡树式写法和线段树式写法。

点击查看二进制分组、平衡树式代码

struct node
{
	int pos[2],val;
}a[500010];
int l[2],r[2],cur;
bool cmp(int x,int y)
{
	return a[x].pos[cur]<a[y].pos[cur];
}
struct KDT
{
	int root[25],s[500010],top=0;
	struct kd_tree
	{
		int ls,rs,val,sum,pos[2],mx[2],mn[2];
	}tree[500010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		tree[rt].val=tree[rt].sum=a[id].val;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum+tree[rt].val;
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(s+l,s+mid,s+r+1,cmp);  rt=build_rt(s[mid]);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	void assign(int &rt)
	{
		if(rt==0)  return;
		top++;  s[top]=rt;
		assign(lson(rt));  assign(rson(rt));
		rt=0;
	}
	void insert(int id)
	{
		top=1;  s[top]=id;
		for(int i=0;i<=20;i++)
		{
			if(root[i]==0)
			{
				build(root[i],1,top,0);
				break;
			}
			else  assign(root[i]);
		}
	}
	int getsum(int rt,int l[],int r[])
	{
		if(rt==0)  return 0;
		for(int i=0;i<=1;i++)  if(l[i]>tree[rt].mx[i]||r[i]<tree[rt].mn[i])  return 0//无交;
		int flag=1;
		for(int i=0;i<=1;i++)  flag&=(l[i]<=tree[rt].mn[i]&&tree[rt].mx[i]<=r[i]);
		if(flag==1)  return tree[rt].sum;//完全包含
		flag=1;
		for(int i=0;i<=1;i++)  flag&=(l[i]<=tree[rt].pos[i]&&tree[rt].pos[i]<=r[i]);
		return flag*tree[rt].val+getsum(lson(rt),l,r)+getsum(rson(rt),l,r);
	}
	int query(int l[],int r[])
	{
		int ans=0;
		for(int i=0;i<=20;i++)  ans+=getsum(root[i],l,r);//直接在每棵树上移动
		return ans;
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,pd,ans=0;
	scanf("%d",&n);  n=0;
	while(scanf("%d",&pd))
	{
		if(pd==1)
		{
			n++;  scanf("%d%d%d",&a[n].pos[0],&a[n].pos[1],&a[n].val);
			a[n].pos[0]^=ans;  a[n].pos[1]^=ans;  a[n].val^=ans;
			K.insert(n);
		}
		if(pd==2)
		{
			scanf("%d%d%d%d",&l[0],&l[1],&r[0],&r[1]);
			l[0]^=ans;  l[1]^=ans;  r[0]^=ans;  r[1]^=ans;
			printf("%d\n",ans=K.query(l,r));
		}
		if(pd==3)  break;
	}
	return 0;
}

luogu P4224 [清华集训 2017] 简单数据结构

详见 2025多校冲刺省选模拟赛15 T3 C. 小 F 的序列。

luogu P7883 平面最近点对（加强加强版）

多倍经验： luogu P1429 平面最近点对（加强版） | luogu P1257 平面上的最接近点对
邻域查询
- 首先建出包含这 \(n\) 个点的 \(KD-Tree\) ，考虑对于每个节点找到不等于该节点且距离最小的节点。
- 使用 \(KD-Tree\) 求解平面最近点对的单次最坏时间复杂度仍为 \(O(n)\) ，需要进一步剪枝。
  - 最优性剪枝：记录子树内部每一维坐标的最大值和最小值，若子树内最优答案都不如已经搜索到的答案优则不搜索其内部。
  - 启发式搜索：若两个儿子的子树内都有可能包含答案，先在与查询点距离（估价函数设为到子树子矩形的最近距离）最近的一个子树中搜索答案，注意在实现估价函数时要考虑查询点在区间内部的情况。
  - 通过计算方差来使得每次都以差别大的维度来作为标准建树。

略带卡常，多交几发就过了。

点击查看代码

const ll inf=0x7f7f7f7f7f7f7f7f;
struct node
{
	double pos[2];
}a[400010];
int cur;
ll ans=inf;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
ll get_dis(int x,int y)
{
	return (a[x].pos[0]-a[y].pos[0])*(a[x].pos[0]-a[y].pos[0])+
		(a[x].pos[1]-a[y].pos[1])*(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root;
	struct kd_tree
	{
		int ls,rs,pos[2],mx[2],mn[2];
	}tree[400010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	double get_var(int l,int r,int op)
	{
		double sum=0,ans=0;
		for(int i=l;i<=r;i++)  sum+=a[i].pos[op];
		sum/=(r-l+1);
		for(int i=l;i<=r;i++)  ans+=(a[i].pos[op]-sum)*(a[i].pos[op]-sum);
		return ans;
	}
	void build(int &rt,int l,int r)
	{
		int mid=(l+r)/2;  cur=(get_var(l,r,1)>get_var(l,r,0));
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1);
		if(mid+1<=r)  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	ll cost(int rt,int pos)
	{
		ll ans=0;
		for(int i=0;i<=1;i++)
		{
			if(a[pos].pos[i]<tree[rt].mn[i])  ans+=1ll*(tree[rt].mn[i]-a[pos].pos[i])*(tree[rt].mn[i]-a[pos].pos[i]);
			if(a[pos].pos[i]>tree[rt].mx[i])  ans+=1ll*(tree[rt].mx[i]-a[pos].pos[i])*(tree[rt].mx[i]-a[pos].pos[i]);
		}
		return ans;
	}
	void query(int rt,int l,int r,int pos)
	{
		int mid=(l+r)/2;
		if(rt!=pos)  ans=min(ans,get_dis(rt,pos));
		ll fl=((l<=mid-1)?cost(lson(rt),pos):inf);
		ll fr=((mid+1<=r)?cost(rson(rt),pos):inf); 
		if(fl<ans&&fr<ans)
		{
			if(fl<fr)
			{
				query(lson(rt),l,mid-1,pos);
				if(fr<ans)  query(rson(rt),mid+1,r,pos);
			}
			else
			{
				query(rson(rt),mid+1,r,pos);
				if(fl<ans)  query(lson(rt),l,mid-1,pos);
			}
		}
		else  if(fl<ans)  query(lson(rt),l,mid-1,pos);
		else  if(fr<ans)  query(rson(rt),mid+1,r,pos);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,i;
	scanf("%d",&n);
	for(i=1;i<=n;i++)  scanf("%lf%lf",&a[i].pos[0],&a[i].pos[1]);
	K.build(K.root,1,n);
	for(i=1;i<=n;i++)  K.query(K.root,1,n,i);
	printf("%.4lf\n",sqrt(ans));
	return 0;
}

3.30

闲话

早上有体活。
上午 \(field\) 嫌机房太闷了遂说让我们 \(10:10 \sim 10:30\) 去外面活动一下，但要是被查到了他不管。
下午到机房后 \(huge\) 说让我们注意机房卫生，衣服统一挂到前面的衣架上，就不要放到旁边的桌子上了；现在还是类似 \(whk\) 的管理模式，禁止携带水果、零食、饮料，特别是辣条类食品，等到后面集训时期会给我们单独时间吃水果用于放松；及时清理桌子上的废纸，要是没位置放书了可以放到前面的书柜里，保证桌面的整洁，虽然 \(miaomiao\) 和 \(field\) 对此要求较少，但还是不定时会有领导来视察；现在仅凭兴趣坚持着走下去可能就不太行了，要找到更深层次自己坚持下去的原因；这届高二出现的问题我们就不能再犯了，严禁在机房打游戏、看小说的现象；我们自己也都知道国家实行双休的意义，要真每周放两天假，网络上还有那么多诱惑我们的东西，我们还能管得住自己在家认真复习吗，差距就是这么越拉越大的，虽说等到高考结束后只能上个专科可能不太大，但要是真发生在自己的身上，我们要想好自己打算继续怎么做；总说和别人比在某个题库上刷了几千道题，或者打了几十场模拟赛也没用，真正管用的是自己总结的一些经验；让我们经常总结下遇到的经验，不至于换个题目背景就又不会了；认真对待以后的每一次比赛，都真正用心去打；经常反思一下自己奥赛学习为什么不如别人，可以找同桌、同宿舍的、上下铺多交流下想法。
\(field\) 给他们说现在以学知识为主，不用太在意一些比赛，后期集训期间比赛强度会很大，大约为一周四、五场。
\(18:15\) 时 \(field\) 让打扫机房，然后就直接提前吃饭了。
晚二让全体到操场排练远足启动仪式，交代了部分细节。结束的时候年级主任说为了为远足储备体力，各班体委组织同学每天早上进行锻炼，并实名登记。
晚三的时候班主任给放了雷军在雷军班上的讲话。

做题纪要

luogu P2479 [SDOI2010] 捉迷藏

跑两边分别求最大距离和最小距离即可。

点击查看代码

const int inf=0x7f7f7f7f;
struct node
{
	int pos[2];
}a[100010];
int cur,ans=inf;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
int get_dis(int x,int y)
{
	return abs(a[x].pos[0]-a[y].pos[0])+abs(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root;
	struct kd_tree
	{
		int ls,rs,pos[2],mx[2],mn[2];
	}tree[100010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	int cost1(int rt,int pos)
	{
		int ans=0;
		for(int i=0;i<=1;i++)  ans+=max(abs(tree[rt].mx[i]-a[pos].pos[i]),
										abs(tree[rt].mn[i]-a[pos].pos[i]));
		return ans;
	}
	int cost2(int rt,int pos)
	{
		int ans=0;
		for(int i=0;i<=1;i++)
		{
			if(a[pos].pos[i]<tree[rt].mn[i])  ans+=tree[rt].mn[i]-a[pos].pos[i];
			if(a[pos].pos[i]>tree[rt].mx[i])  ans+=a[pos].pos[i]-tree[rt].mx[i];
		}
		return ans;
	}
	void query1(int rt,int l,int r,int pos,int &ans)
	{
		int mid=(l+r)/2;
		if(rt!=pos)  ans=max(ans,get_dis(rt,pos));
		int fl=((l<=mid-1)?cost1(lson(rt),pos):-inf);
		int fr=((mid+1<=r)?cost1(rson(rt),pos):-inf);
		if(fl>ans&&fr>ans)  
		{
			if(fl>fr)
			{
				query1(lson(rt),l,mid-1,pos,ans);
				if(fr>ans)  query1(rson(rt),mid+1,r,pos,ans);
			}
			else
			{
				query1(rson(rt),mid+1,r,pos,ans);
				if(fl>ans)  query1(lson(rt),l,mid-1,pos,ans);
			}
		}
		else  if(fl>ans)  query1(lson(rt),l,mid-1,pos,ans);
		else  if(fr>ans)  query1(rson(rt),mid+1,r,pos,ans);
	}
	void query2(int rt,int l,int r,int pos,int &ans)
	{
		int mid=(l+r)/2;
		if(rt!=pos)  ans=min(ans,get_dis(rt,pos));
		int fl=((l<=mid-1)?cost2(lson(rt),pos):inf);
		int fr=((mid+1<=r)?cost2(rson(rt),pos):inf);
		if(fl<ans&&fr<ans)  
		{
			if(fl<fr)
			{
				query2(lson(rt),l,mid-1,pos,ans);
				if(fr<ans)  query2(rson(rt),mid+1,r,pos,ans);
			}
			else
			{
				query2(rson(rt),mid+1,r,pos,ans);
				if(fl<ans)  query2(lson(rt),l,mid-1,pos,ans);
			}
		}
		else  if(fl<ans)  query2(lson(rt),l,mid-1,pos,ans);
		else  if(fr<ans)  query2(rson(rt),mid+1,r,pos,ans);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,ans=inf,up,down,i;
	cin>>n;
	for(i=1;i<=n;i++)  cin>>a[i].pos[0]>>a[i].pos[1];
	K.build(K.root,1,n,0);
	for(i=1;i<=n;i++)  
	{
		up=-inf;  K.query1(K.root,1,n,i,up);
		down=inf;  K.query2(K.root,1,n,i,down);
		ans=min(ans,up-down);
	}
	cout<<ans<<endl;
	return 0;
}

LibreOJ 2043. 「CQOI2016」K 远点对

开一个大小为 \(2k\) 的堆即可。

点击查看代码

struct node
{
	int pos[2];
}a[100010];
int cur,k;
priority_queue<ull,vector<ull>,greater<ull> >q;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
ull get_dis(int x,int y)
{
	return 1ull*(a[x].pos[0]-a[y].pos[0])*(a[x].pos[0]-a[y].pos[0])+
			1ull*(a[x].pos[1]-a[y].pos[1])*(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root;
	struct kd_tree
	{
		int ls,rs,pos[2],mx[2],mn[2];
	}tree[100010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	ull cost(int rt,int pos)
	{
		ull ans=0;
		for(int i=0;i<=1;i++)
		{ 
			ans+=max(1ull*(tree[rt].mx[i]-a[pos].pos[i])*(tree[rt].mx[i]-a[pos].pos[i]),
					1ull*(tree[rt].mn[i]-a[pos].pos[i])*(tree[rt].mn[i]-a[pos].pos[i]));
		}
		return ans;
	}
	void query(int rt,int l,int r,int pos)
	{
		int mid=(l+r)/2;
		if(rt!=pos&&get_dis(rt,pos)>q.top())
		{
			q.pop();  q.push(get_dis(rt,pos));
		}
		ull fl=((l<=mid-1)?cost(lson(rt),pos):0);
		ull fr=((mid+1<=r)?cost(rson(rt),pos):0); 
		if(fl>q.top()&&fr>q.top())
		{
			if(fl>fr)
			{
				query(lson(rt),l,mid-1,pos);
				if(fr>q.top())  query(rson(rt),mid+1,r,pos);
			}
			else
			{
				query(rson(rt),mid+1,r,pos);
				if(fl>q.top())  query(lson(rt),l,mid-1,pos);
			}
		}
		else  if(fl>q.top())  query(lson(rt),l,mid-1,pos);
		else  if(fr>q.top())  query(rson(rt),mid+1,r,pos);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,k,i;
	cin>>n>>k;  k*=2;
	for(i=1;i<=n;i++)  cin>>a[i].pos[0]>>a[i].pos[1];
	for(i=1;i<=k;i++)  q.push(0);
	K.build(K.root,1,n,0);
	for(i=1;i<=n;i++)  K.query(K.root,1,n,i);
	cout<<q.top()<<endl;
	return 0;
}

luogu P6247 [SDOI2012] 最近最远点对

跑两边分别求最大距离和最小距离即可。

点击查看代码

const double inf=2e18;
struct node
{
	double pos[2];
}a[400010];
int cur;
double ans=inf;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
double get_dis(int x,int y)
{
	return (a[x].pos[0]-a[y].pos[0])*(a[x].pos[0]-a[y].pos[0])+
		(a[x].pos[1]-a[y].pos[1])*(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root;
	struct kd_tree
	{
		int ls,rs,pos[2],mx[2],mn[2];
	}tree[400010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	double get_var(int l,int r,int op)
	{
		double sum=0,ans=0;
		for(int i=l;i<=r;i++)  sum+=a[i].pos[op];
		sum/=(r-l+1);
		for(int i=l;i<=r;i++)  ans+=(a[i].pos[op]-sum)*(a[i].pos[op]-sum);
		return ans;
	}
	void build(int &rt,int l,int r)
	{
		int mid=(l+r)/2;  cur=(get_var(l,r,1)>get_var(l,r,0));
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1);
		if(mid+1<=r)  build(rson(rt),mid+1,r);
		pushup(rt);
	}
	double cost1(int rt,int pos)
	{
		double ans=0;
		for(int i=0;i<=1;i++)
		{
			if(a[pos].pos[i]<tree[rt].mn[i])  ans+=(tree[rt].mn[i]-a[pos].pos[i])*(tree[rt].mn[i]-a[pos].pos[i]);
			if(a[pos].pos[i]>tree[rt].mx[i])  ans+=(tree[rt].mx[i]-a[pos].pos[i])*(tree[rt].mx[i]-a[pos].pos[i]);
		}
		return ans;
	}
	double cost2(int rt,int pos)
	{
		double ans=0;
		for(int i=0;i<=1;i++)
		{
			ans+=max((tree[rt].mx[i]-a[pos].pos[i])*(tree[rt].mx[i]-a[pos].pos[i]),
					(tree[rt].mn[i]-a[pos].pos[i])*(tree[rt].mn[i]-a[pos].pos[i]));
		}
		return ans;
	}
	void query1(int rt,int l,int r,int pos)
	{
		int mid=(l+r)/2;
		if(rt!=pos)  ans=min(ans,get_dis(rt,pos));
		double fl=((l<=mid-1)?cost1(lson(rt),pos):inf);
		double fr=((mid+1<=r)?cost1(rson(rt),pos):inf); 
		if(fl<ans&&fr<ans)
		{
			if(fl<fr)
			{
				query1(lson(rt),l,mid-1,pos);
				if(fr<ans)  query1(rson(rt),mid+1,r,pos);
			}
			else
			{
				query1(rson(rt),mid+1,r,pos);
				if(fl<ans)  query1(lson(rt),l,mid-1,pos);
			}
		}
		else  if(fl<ans)  query1(lson(rt),l,mid-1,pos);
		else  if(fr<ans)  query1(rson(rt),mid+1,r,pos);
	}
	void query2(int rt,int l,int r,int pos)
	{
		int mid=(l+r)/2;
		if(rt!=pos)  ans=max(ans,get_dis(rt,pos));
		double fl=((l<=mid-1)?cost2(lson(rt),pos):-inf);
		double fr=((mid+1<=r)?cost2(rson(rt),pos):-inf); 
		if(fl>ans&&fr>ans)  
		{
			if(fl>fr)
			{
				query2(lson(rt),l,mid-1,pos);
				if(fr>ans)  query2(rson(rt),mid+1,r,pos);
			}
			else
			{
				query2(rson(rt),mid+1,r,pos);
				if(fl>ans)  query2(lson(rt),l,mid-1,pos);
			}
		}
		else  if(fl>ans)  query2(lson(rt),l,mid-1,pos);
		else  if(fr>ans)  query2(rson(rt),mid+1,r,pos);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,i;
	scanf("%d",&n);
	for(i=1;i<=n;i++)  scanf("%lf%lf",&a[i].pos[0],&a[i].pos[1]);
	K.build(K.root,1,n);
	for(i=1;i<=n;i++)  K.query1(K.root,1,n,i);
	printf("%.4lf ",sqrt(ans));
	ans=-inf;
	for(i=1;i<=n;i++)  K.query2(K.root,1,n,i);
	printf("%.4lf\n",sqrt(ans));
	return 0;
}

luogu P2093 [国家集训队] JZPFAR

记录下答案的来源即可。

点击查看代码

struct node
{
	int pos[2],id;
}a[110010];
int cur;
struct quality
{
	ll dis,id;
	bool operator < (const quality &another) const
	{
		return (dis==another.dis)?(id<another.id):(dis>another.dis);
	}
	bool operator > (const quality &another) const
	{
		return (dis==another.dis)?(id<another.id):(dis>another.dis);
	}
};
priority_queue<quality>q;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
ll get_dis(int x,int y)
{
	return 1ll*(a[x].pos[0]-a[y].pos[0])*(a[x].pos[0]-a[y].pos[0])+
			1ll*(a[x].pos[1]-a[y].pos[1])*(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root;
	struct kd_tree
	{
		int ls,rs,id,pos[2],mx[2],mn[2];
	}tree[100010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		tree[rt].id=a[id].id;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	ll cost(int rt,int pos)
	{
		ll ans=0;
		for(int i=0;i<=1;i++)
		{
			ans+=max(1ll*(tree[rt].mx[i]-a[pos].pos[i])*(tree[rt].mx[i]-a[pos].pos[i]),
					1ll*(tree[rt].mn[i]-a[pos].pos[i])*(tree[rt].mn[i]-a[pos].pos[i]));
		}
		return ans;
	}
	void query(int rt,int l,int r,int pos)
	{
		int mid=(l+r)/2;
		quality tmp={get_dis(rt,pos),tree[rt].id};
		if(tmp>q.top())
		{
			q.pop();  q.push(tmp);
		}
		ll fl=((l<=mid-1)?cost(lson(rt),pos):-1);
		ll fr=((mid+1<=r)?cost(rson(rt),pos):-1);
		if(fl>=q.top().dis&&fr>=q.top().dis)
		{
			if(fl>=fr)
			{
				query(lson(rt),l,mid-1,pos);
				if(fr>=q.top().dis)  query(rson(rt),mid+1,r,pos);
			}
			else
			{
				query(rson(rt),mid+1,r,pos);
				if(fl>=q.top().dis)  query(lson(rt),l,mid-1,pos);
			}
		}
		else  if(fl>=q.top().dis)  query(lson(rt),l,mid-1,pos);
		else  if(fr>=q.top().dis)  query(rson(rt),mid+1,r,pos);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,k,i,j;
	cin>>n;
	for(i=1;i<=n;i++)
	{
		cin>>a[i].pos[0]>>a[i].pos[1];  a[i].id=i;
	}
	K.build(K.root,1,n,0);
	cin>>m;
	for(i=1;i<=m;i++)
	{
		cin>>a[n+i].pos[0]>>a[n+i].pos[1]>>k;
		while(q.empty()==0)  q.pop();
		for(j=1;j<=k;j++)  q.push((quality){0,0});
		K.query(K.root,1,n,n+i);
		cout<<q.top().id<<endl;
	}
	return 0;
}

luogu P7561 [JOISC 2021] 道路の建設案 (Road Construction) (Day2)

多倍经验： AT_joisc2021_e 道路の建設案 (Road Construction)

输出答案时跳着取即可。

点击查看代码

const ll inf=0x7f7f7f7f7f7f7f7f;
struct node
{
	int pos[2];
}a[250010];
int cur,cnt=0;
ll ans[250010];
priority_queue<ll>q;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
ll get_dis(int x,int y)
{
	return llabs(a[x].pos[0]-a[y].pos[0])+llabs(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root;
	struct kd_tree
	{
		int ls,rs,pos[2],mx[2],mn[2];
	}tree[250010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	ll cost(int rt,int pos)
	{
		ll ans=0;
		for(int i=0;i<=1;i++)
		{
			if(a[pos].pos[i]<tree[rt].mn[i])  ans+=tree[rt].mn[i]-a[pos].pos[i];
			if(a[pos].pos[i]>tree[rt].mx[i])  ans+=a[pos].pos[i]-tree[rt].mx[i];
		}
		return ans;
	}
	void query(int rt,int l,int r,int pos)
	{
		int mid=(l+r)/2;
		if(rt!=pos&&get_dis(rt,pos)<q.top())
		{
			q.pop();  q.push(get_dis(rt,pos));
		}
		ll fl=((l<=mid-1)?cost(lson(rt),pos):inf);
		ll fr=((mid+1<=r)?cost(rson(rt),pos):inf); 
		if(fl<q.top()&&fr<q.top())
		{
			if(fl<fr)
			{
				query(lson(rt),l,mid-1,pos);
				if(fr<q.top())  query(rson(rt),mid+1,r,pos);
			}
			else
			{
				query(rson(rt),mid+1,r,pos);
				if(fl<q.top())  query(lson(rt),l,mid-1,pos);
			}
		}
		else  if(fl<q.top())  query(lson(rt),l,mid-1,pos);
		else  if(fr<q.top())  query(rson(rt),mid+1,r,pos);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,k,i;
	cin>>n>>k;  k*=2;
	for(i=1;i<=n;i++)  cin>>a[i].pos[0]>>a[i].pos[1];
	for(i=1;i<=k;i++)  q.push(inf);
	K.build(K.root,1,n,0);
	for(i=1;i<=n;i++)  K.query(K.root,1,n,i);
	for(i=k;i>=1;i--)
	{
		ans[i]=q.top();  q.pop();
	}
	for(i=1;i<=k;i+=2)  cout<<ans[i]<<endl;
	return 0;
}

luogu P4475 巧克力王国

将 \((x,y)\) 看做二维平面上的点，若 \(\max \{ x \},\min \{ x \},\max \{ y \},\min \{ y \}\) 自由组合都符合条件则直接返回子树信息。

点击查看代码

struct node
{
	ll pos[2],val;
}a[50010];
ll cur;
bool cmp(node x,node y)
{
	return x.pos[cur]<y.pos[cur];
}
ll f(ll a,ll b,ll x,ll y)
{
	return a*x+b*y;
}
struct KDT
{
	ll root;
	struct kd_tree
	{
		ll ls,rs,val,sum,pos[2],mx[2],mn[2];
	}tree[50010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	ll build_rt(ll id)
	{
		ll rt=id;
		lson(rt)=rson(rt)=0;
		tree[rt].val=tree[rt].sum=a[id].val;
		for(ll i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return id;
	}
	void pushup(ll rt)
	{
		tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum+tree[rt].val;
		for(ll i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(ll &rt,ll l,ll r,ll dir)
	{
		ll mid=(l+r)/2;  cur=dir;
		nth_element(a+l,a+mid,a+r+1,cmp);  rt=build_rt(mid);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	ll query(ll rt,ll a,ll b,ll c)
	{
		if(rt==0)  return 0;
		ll flag=1;
		flag&=(f(a,b,tree[rt].mx[0],tree[rt].mn[1])<c);  flag&=(f(a,b,tree[rt].mx[0],tree[rt].mx[1])<c);
		flag&=(f(a,b,tree[rt].mn[0],tree[rt].mn[1])<c);  flag&=(f(a,b,tree[rt].mn[0],tree[rt].mx[1])<c);
		if(flag==1)  return tree[rt].sum;
		flag|=(f(a,b,tree[rt].mx[0],tree[rt].mn[1])<c);  flag|=(f(a,b,tree[rt].mx[0],tree[rt].mx[1])<c);
		flag|=(f(a,b,tree[rt].mn[0],tree[rt].mn[1])<c);  flag|=(f(a,b,tree[rt].mn[0],tree[rt].mx[1])<c);
		if(flag==0)  return 0;
		flag=(f(a,b,tree[rt].pos[0],tree[rt].pos[1])<c);
		return flag*tree[rt].val+query(lson(rt),a,b,c)+query(rson(rt),a,b,c);
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,x,y,z,i;
	cin>>n>>m;
	for(i=1;i<=n;i++)  cin>>a[i].pos[0]>>a[i].pos[1]>>a[i].val;
	K.build(K.root,1,n,0);
	for(i=1;i<=m;i++)
	{
		cin>>x>>y>>z;
		cout<<K.query(K.root,x,y,z)<<endl;
	}
	return 0;
}

luogu P4169 [Violet] 天使玩偶/SJY摆棋子

在 luogu P7561 [JOISC 2021] 道路の建設案 (Road Construction) (Day2) 的基础上套个二进制分组即可。

点击查看代码

const int inf=0x3f3f3f3f;
struct node
{
	int pos[2];
}a[1000010];
int cur,ans;
bool cmp(int x,int y)
{
	return a[x].pos[cur]<a[y].pos[cur];
}
int get_dis(int x,int y)
{
	return abs(a[x].pos[0]-a[y].pos[0])+abs(a[x].pos[1]-a[y].pos[1]);
}
struct KDT
{
	int root[25],s[1000010],top=0;
	struct kd_tree
	{
		int ls,rs,pos[2],mx[2],mn[2];
	}tree[1000010];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(s+l,s+mid,s+r+1,cmp);  rt=build_rt(s[mid]);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	void assign(int &rt)
	{
		if(rt==0)  return;
		top++;  s[top]=rt;
		assign(lson(rt));  assign(rson(rt));
		rt=0;
	}
	void insert(int id)
	{
		top=1;  s[top]=id;
		for(int i=0;i<=21;i++)
		{
			if(root[i]==0)
			{
				build(root[i],1,top,0);
				break;
			}
			else  assign(root[i]);
		}
	}
	int cost(int rt,int pos)
	{
		if(rt==0)  return inf;
		int ans=0;
		for(int i=0;i<=1;i++)
		{
			if(a[pos].pos[i]<tree[rt].mn[i])  ans+=tree[rt].mn[i]-a[pos].pos[i];
			if(a[pos].pos[i]>tree[rt].mx[i])  ans+=a[pos].pos[i]-tree[rt].mx[i];
		}
		return ans;
	}
	void getsum(int rt,int pos)
	{
		if(rt==0)  return;
		ans=min(ans,get_dis(rt,pos));
		int fl=cost(lson(rt),pos),fr=cost(rson(rt),pos);
		if(fl<ans&&fr<ans)
		{
			if(fl<fr)
			{
				getsum(lson(rt),pos);
				if(fr<ans)  getsum(rson(rt),pos);
			}
			else
			{
				getsum(rson(rt),pos);
				if(fl<ans)  getsum(lson(rt),pos);
			}
		}
		else  if(fl<ans)  getsum(lson(rt),pos);
		else  if(fr<ans)  getsum(rson(rt),pos);
	}
	int query(int pos)
	{
		ans=inf;
		for(int i=0;i<=21;i++)  getsum(root[i],pos);
		return ans;
	}
}K;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,pd,x,y,i;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].pos[0],&a[i].pos[1]);
		K.insert(i);
	}
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&pd,&x,&y);
		if(pd==1)
		{
			n++;  a[n].pos[0]=x;  a[n].pos[1]=y;
			K.insert(n);
		}
		else
		{
			a[0].pos[0]=x;  a[0].pos[1]=y;
			printf("%d\n",K.query(0));
		}
	}
	return 0;
}

luogu P12004 【MX-X10-T0】[LSOT-4] 嗯欧哎劈

分支结构。

点击查看代码

int a[50];
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,i;
	cin>>n;
	for(i=1;i<=32;i++)  cin>>a[i];
	if(n>=a[1])  cout<<"sidekick"<<endl;
	else  if(n>=a[3]-1)  cout<<"sgnd"<<endl;
	else  if(n>=40)  cout<<"cxq"<<endl;
	else  cout<<"kiku"<<endl;
	return 0;
}

luogu P12005 【MX-X10-T1】[LSOT-4] 如何用中间忘了写一篇排版整齐的题解？

循环结构。

点击查看代码

char s[110];
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif	
	int n,flag=0,last1=0,last2=0,x,i,j;
	cin>>(s+1);  n=strlen(s+1);
	for(i=1;i<=n;i++)
	{
		if(s[i]=='@'&&(s[i-1]=='a'||s[i-1]=='1'||s[i-1]=='$'))  flag=1;
		if(s[i]=='a'||s[i]=='1'||s[i]=='$')  last1=i;
		if(s[i]==',')  last2=i;
		if(last1!=0&&s[i]==',')
		{
			x=(last1+1<=i-1);
			for(j=last1+1;j<=i-1;j++)  x&=(s[j]=='_');
			if(x==1)  flag=1;
		}
		if(last2!=0&&(s[i]=='a'||s[i]=='1'||s[i]=='$'))
		{
			x=(last2+1<=i-1);
			for(j=last2+1;j<=i-1;j++)  x&=(s[j]=='_');
			if(x==1)  flag=1;
		}
	}
	cout<<((flag==1)?"No":"Yes")<<endl;
	return 0;
}

luogu P4848 崂山白花蛇草水

将 \(x,y,v\) 看做下标后二分答案使用 \(KD-Tree\) 维护三维偏序进行 \(check\) 的时间复杂度为 \(O(q \log^{2} q+q^{\frac{5}{3}} \log V)\) ，无法接受。
观察到 \(q^{\frac{3}{2}}\) 或许可以接受，考虑减少一维使用其他数据结构维护。

外层动态开点线段树套内层 \(KD-Tree\) 并使用线段树上二分即可，时间复杂度为 \(O(q \log^{2} q \log V+q^{\frac{3}{2}} \log V)\) .

点击查看代码

const int inf=1000000000;
struct node
{
	int pos[2];
}a[100010<<5];
int st[2],ed[2],cur,n;
bool cmp(int x,int y)
{
	return a[x].pos[cur]<a[y].pos[cur];
}
struct KDT
{
	int root[100010<<5][18],s[100010],top;
	struct kd_tree
	{
		int ls,rs,siz,val,pos[2],mx[2],mn[2];
	}tree[100010<<5];
	#define lson(rt) (tree[rt].ls)
	#define rson(rt) (tree[rt].rs)
	int build_rt(int id)
	{
		int rt=id;
		lson(rt)=rson(rt)=0;
		for(int i=0;i<=1;i++)
			tree[rt].pos[i]=tree[rt].mx[i]=tree[rt].mn[i]=a[id].pos[i];
		return rt;
	}
	void pushup(int rt)
	{
		tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+1;
		for(int i=0;i<=1;i++)
		{
			tree[rt].mx[i]=tree[rt].mn[i]=tree[rt].pos[i];
			if(lson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[lson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[lson(rt)].mn[i]);
			}
			if(rson(rt)!=0)
			{
				tree[rt].mx[i]=max(tree[rt].mx[i],tree[rson(rt)].mx[i]);
				tree[rt].mn[i]=min(tree[rt].mn[i],tree[rson(rt)].mn[i]);
			}
		}
	}
	void build(int &rt,int l,int r,int dir)
	{
		int mid=(l+r)/2;  cur=dir;
		nth_element(s+l,s+mid,s+r+1,cmp);   rt=build_rt(s[mid]);
		if(l<=mid-1)  build(lson(rt),l,mid-1,dir^1);
		if(mid+1<=r)  build(rson(rt),mid+1,r,dir^1);
		pushup(rt);
	}
	void assign(int &rt)
	{
		if(rt==0)  return;
		top++;  s[top]=rt;
		assign(lson(rt));  assign(rson(rt));
		rt=0;
	}
	void insert(int rt,int id)
	{ 
		top=1;  s[top]=id;
		for(int i=0;i<=17;i++)
		{
			if(root[rt][i]==0)
			{	
				build(root[rt][i],1,top,0);
				break;
			}
			else  assign(root[rt][i]);
		}
	}
	int getsum(int rt,int l[2],int r[2])
	{
		if(rt==0)  return 0;
		int flag=1;
		for(int i=0;i<=1;i++)  flag&=(l[i]<=tree[rt].mn[i]&&tree[rt].mx[i]<=r[i]);
		if(flag==1)  return tree[rt].siz;
		for(int i=0;i<=1;i++)  if(l[i]>tree[rt].mx[i]||r[i]<tree[rt].mn[i])  return 0;
		flag=1;
		for(int i=0;i<=1;i++)  flag&=(l[i]<=tree[rt].pos[i]&&tree[rt].pos[i]<=r[i]);
		return flag+getsum(lson(rt),l,r)+getsum(rson(rt),l,r);
	}
	int query(int rt,int l[2],int r[2])
	{
		int ans=0;
		for(int i=0;i<=17;i++)  ans+=getsum(root[rt][i],l,r);
		return ans;
	}
}K;
struct SMT
{	
	struct SegmentTree
	{
		int ls,rs;
	}tree[100010<<5];
	int root,rt_sum=0;
	int build_rt()
	{
		rt_sum++;
		return rt_sum;
	}
	void update(int &rt,int l,int r,int pos)
	{
		if(rt==0)  rt=build_rt();
		K.insert(rt,n);
		if(l==r)  return;
		n++;  a[n]=a[n-1];
		int mid=(l+r)/2;
		if(pos<=mid)  update(lson(rt),l,mid,pos);
		else  update(rson(rt),mid+1,r,pos);
	}
	int query(int rt,int l,int r,int k)
	{
		if(rt==0)  return 0;
		if(l==r)  return (K.query(rt,st,ed)>=k)*l;
		int mid=(l+r)/2,sum=K.query(rson(rt),st,ed);
		if(sum>=k)  return query(rson(rt),mid+1,r,k);
		else  return query(lson(rt),l,mid,k-sum);
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int m,pd,x,y,z,ans=0,i;
	cin>>n>>m;  n=0;
	for(i=1;i<=m;i++)
	{
		cin>>pd>>x>>y;   x^=ans;  y^=ans;
		if(pd==1)
		{
			n++;  a[n].pos[0]=x;  a[n].pos[1]=y;
			cin>>z;  z^=ans;
			T.update(T.root,1,inf,z);
		}
		else
		{
			st[0]=x;  st[1]=y;
			cin>>ed[0]>>ed[1]>>z;  ed[0]^=ans;  ed[1]^=ans;  z^=ans;
			ans=T.query(T.root,1,inf,z);
			if(ans==0)  cout<<"NAIVE!ORZzyz."<<endl;
			else  cout<<ans<<endl;
		}
	} 
	return 0;
}

[ABC399F] Range Power Sum

考虑二项式定理将幂次展开，设 \(f_{r,i}\) 表示 \(\sum\limits_{l=1}^{r}(\sum\limits_{j=l}^{r}a_{j})^{i}\) ，最终有 \(\sum\limits_{i=1}^{n}f_{n,k}\) 即为所求。
推一下式子，有 \(\begin{aligned} f_{r,i} &=a_{r}^{i}+\sum\limits_{l=1}^{r-1}(a_{r}+\sum\limits_{j=l}^{r-1}a_{j})^{i} \\ &=a_{r}^{i}+\sum\limits_{l=1}^{r-1}\sum\limits_{j=0}^{i}\dbinom{i}{j}a_{r}^{i-j}(\sum\limits_{h=l}^{r-1}a_{h})^{j} \\ &=a_{r}^{i}+\sum\limits_{j=0}^{i}\dbinom{i}{j}a_{r}^{i-j}f_{r-1,j} \end{aligned}\) 。

暴力转移即可，可以使用 NTT 优化。

点击查看代码

const ll p=998244353;
ll a[200010],C[15][15],f[200010][15];
ll qpow(ll a,ll b,ll p)
{
	ll ans=1;
	while(b)
	{
		if(b&1)  ans=ans*a%p;
		b>>=1;
		a=a*a%p;
	}
	return ans;
}
void init(ll n)
{
	C[0][0]=C[1][0]=C[1][1]=1;
	for(ll i=2;i<=n;i++)
	{
		C[i][0]=1;
		for(ll j=1;j<=i;j++)  C[i][j]=(C[i-1][j-1]+C[i-1][j])%p;
	}
}
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	ll n,m,ans=0,i,j,k;
	cin>>n>>m;  init(m);
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
		for(j=0;j<=m;j++)
		{
			f[i][j]=qpow(a[i],j,p);
			for(k=0;k<=j;k++)  f[i][j]=(f[i][j]+C[j][k]*qpow(a[i],j-k,p)%p*f[i-1][k]%p)%p;
		}
		ans=(ans+f[i][m])%p;
	}
	cout<<ans<<endl;
	return 0;
}

luogu P8264 [Ynoi Easy Round 2020] TEST_100

详见 8.数据结构 G luogu P8264 [Ynoi Easy Round 2020] TEST_100 。

luogu P10284 [USACO24OPEN] Splitting Haybales P

令 \(F_{i}(x)=\begin{cases} x-a_{i} & x>0 \\ x+a_{i} & x \le 0 \end{cases}\) 后离线做即可。

点击查看代码

struct node
{
	int pos,id,x;
}ql[200010],qr[200010];
int it[200010],a[200010],ans[200010];
mt19937 rng(random_device{}());
bool cmp(node a,node b)
{
	return a.pos<b.pos;
}
struct BST
{
	int id[200010],root,rt_sum;
	struct FHQ_Treap
	{
		int son[2],fa,rnd,cnt,siz,val,mx,mn,add;
	}tree[200010];
	#define lson(rt) (tree[rt].son[0])
	#define rson(rt) (tree[rt].son[1])
	#define fa(rt) (tree[rt].fa)
	int find(int x)
	{
		return id[x]==x?x:id[x]=find(id[x]);
	}
	int build_rt(int val)
	{
		rt_sum++;  int rt=rt_sum;
		lson(rt)=rson(rt)=fa(rt)=tree[rt].add=0;
		tree[rt].val=tree[rt].mx=tree[rt].mn=val;
		tree[rt].rnd=rng();
		tree[rt].cnt=tree[rt].siz=1;
		return id[rt]=rt;
	}
	void pushup(int rt)
	{
		tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt;
		fa(rt)=0;
		if(lson(rt)!=0)
		{
			tree[rt].mn=tree[lson(rt)].mn;
			fa(lson(rt))=rt;
		}
		else  tree[rt].mn=tree[rt].val;
		if(rson(rt)!=0)
		{
			tree[rt].mx=tree[rson(rt)].mx;
			fa(rson(rt))=rt;
		}
		else  tree[rt].mx=tree[rt].val;
	}
	void pushlazy(int rt,int add)
	{
		if(rt==0)  return;
		tree[rt].add+=add;  tree[rt].val+=add;
		tree[rt].mx+=add;  tree[rt].mn+=add;
	}
	void pushdown(int rt)
	{
		pushlazy(lson(rt),tree[rt].add);
		pushlazy(rson(rt),tree[rt].add);
		tree[rt].add=0;
	}
	void split(int rt,int val,int &x,int &y)
	{
		if(rt==0)
		{
			x=y=0;
			return;
		}
		pushdown(rt);
		if(tree[rt].val<=val)
		{
			x=rt;
			split(rson(rt),val,rson(x),y);
		}
		else
		{
			y=rt;
			split(lson(rt),val,x,lson(y));
		}
		pushup(rt);
	}
	int merge(int rt1,int rt2)
	{
		if(rt1==0||rt2==0)  return rt1+rt2;
		pushdown(rt1);  pushdown(rt2);
		if(tree[rt1].rnd<tree[rt2].rnd)
		{
			rson(rt1)=merge(rson(rt1),rt2);
			pushup(rt1);
			return rt1;
		}
		else
		{
			lson(rt2)=merge(rt1,lson(rt2));
			pushup(rt2);
			return rt2;
		}
	}
	int join(int rt1,int rt2)
	{
		if(rt1==0||rt2==0)  return rt1+rt2;
		if(tree[rt1].mn>tree[rt2].mx)  return merge(rt2,rt1);
		if(tree[rt1].mx<tree[rt2].mn)  return merge(rt1,rt2);
		if(tree[rt1].rnd>tree[rt2].rnd)  swap(rt1,rt2);
		pushdown(rt1);  pushdown(rt2);
		int x,y,z;
		split(rt2,tree[rt1].val,x,y);  split(x,tree[rt1].val-1,x,z);
		if(z!=0)
		{
			tree[rt1].cnt+=tree[z].siz;  tree[rt1].siz+=tree[z].siz;
			id[z]=rt1;
		}
		lson(rt1)=join(lson(rt1),x);   rson(rt1)=join(rson(rt1),y);
		pushup(rt1);
		return rt1;
	}
	int insert(int val)
	{
		int x,y,z;
		split(root,val,x,y);
		split(x,val-1,x,z);
		if(z!=0)
		{
			tree[z].cnt++;   tree[z].siz++;
		}
		else  z=build_rt(val);
		root=merge(merge(x,z),y);
		return z;
	}
	void update(int val)
	{
		int x,y;
		split(root,0,x,y);
		pushlazy(x,val);  pushlazy(y,-val);
		root=join(x,y);
	}
	int query(int rt)
	{
		rt=find(rt);
		int ans=tree[rt].val;
		for(int x=fa(rt);x!=0;x=fa(x))  ans+=tree[x].add;
		return ans;
	}
}T;
int main()
{
// #define Isaac
#ifdef Isaac
	freopen("in.in","r",stdin);
	freopen("out.out","w",stdout);
#endif
	int n,m,l,r,x,i,j,k;
	cin>>n;
	for(i=1;i<=n;i++)  cin>>a[i];
	cin>>m;
	for(i=1;i<=m;i++)
	{
		cin>>l>>r>>x;
		ql[i]=(node){l,i,x};  qr[i]=(node){r,i,x};
	}
	sort(ql+1,ql+1+m,cmp);  sort(qr+1,qr+1+m,cmp);
	for(i=j=k=1;i<=n;i++)
	{
		for(;ql[j].pos==i;j++)  it[ql[j].id]=T.insert(ql[j].x);
		T.update(a[i]);
		for(;qr[k].pos==i;k++)  ans[qr[k].id]=T.query(it[qr[k].id]);
	}
	for(i=1;i<=m;i++)  cout<<ans[i]<<endl;
	return 0;
}

3.31

闲话

历史课任务重大： \(8\) 节课需要讲完两本书，还需要保证我们通过学考。这次从原始社会讲到了宋、元的科技成就。

posted @ 2025-03-22 22:10 hzoi_Shadow 阅读(380) 评论(2) 收藏举报

刷新页面返回顶部

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。 纵使世界万般残酷，总有温暖值得守护……

时间错乱

闲话

3.15

闲话

做题纪要

3.18

闲话

做题纪要

3.19

闲话

做题纪要

3.21

闲话

做题纪要

3.22

闲话

做题纪要

3.23

闲话

做题纪要

3.25

闲话

做题纪要

3.26

闲话

做题纪要

3.27

闲话

做题纪要

3.28

闲话

做题纪要

3.29

闲话

做题纪要

3.30

闲话

做题纪要

3.31

闲话

公告

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。纵使世界万般残酷，总有温暖值得守护……