2025省选模拟11

合集 - 高一下二月(18)

1.高一下二月上旬日记02-022.来自aakennes的新年祝福02-033.2025省选模拟902-064.2025多校冲刺省选模拟赛902-065.2025多校冲刺省选模拟赛1002-096.2025省选模拟1002-097.高一下二月中旬日记02-108.2025多校冲刺省选模拟赛1102-149.2025多校冲刺省选模拟赛1202-1410.2025多校冲刺省选模拟赛1302-15

11.2025省选模拟1102-17

12.2025多校冲刺省选模拟赛1402-1813.2025多校冲刺省选模拟赛15 && 2025省选模拟1202-2114.高一下二月下旬日记02-2115.2025省选模拟1302-2216.2025省选模拟1402-2317.2025省选模拟1502-2418.预祝2025省选嗨翻天02-26

收起

2025省选模拟11

题目来源： 2024省选联测22

$T1$ HZTG5881. 送信 $100pts$

• 原题： CF838D Airplane Arrangements

• 部分分

  • $50pts$ ：爆搜。
  点击查看代码

  const ll p=998244353;
  ll vis[5010],ans=0;
  void dfs(ll pos,ll n,ll m)
  {
      if(pos==m+1)  ans=(ans+1)%p;
      else
      {
          for(ll i=1;i<=n;i++)
          {
              for(ll j=i;j>=1;j--)
              {
                  if(vis[j]==0)
                  {
                      vis[j]=1;
                      dfs(pos+1,n,m);
                      vis[j]=0;
                      break;
                  }
              }
              for(ll j=i;j<=n;j++)
              {
                  if(vis[j]==0)
                  {
                      vis[j]=1;
                      dfs(pos+1,n,m);
                      vis[j]=0;
                      break;
                  }
              }
          }
      }
  }
  int main()
  {
  #define Isaac
  #ifdef Isaac
      freopen("postbox.in","r",stdin);
      freopen("postbox.out","w",stdout);
  #endif
      ll n,m,i;
      cin>>n>>m;
      dfs(1,n,m);
      cout<<ans<<endl;
      return 0;
  }
  

• 正解

  • 通过爆搜打出 $n\le 10,m\le 8$ 的表，易得 $2(2n+2{)}^{m-1}(n-m+1)$ 即为所求。

    点击查看打表经过

    

    猜测可能有递推式，可能与对角线有关。

    对于 $m=1$ 的情况，有 $2n$ 即为所求。

    对于 $m=2$ 的情况，发现与左下角的 $2(n+1)=2n+2$ 直接的倍数关系成 $2,4,6,8,\dots$ 变化，有 $2(2n+2)(n-1)=4(n^2-1)$ 即为所求。

    对于 $m=3$ 的情况，其与左下角 $4(n^2-1)$ 基本没什么关系，选择再除掉一个 $2n+2$ ，分别得到 $16,40,72,112,160\dots$ ，差分下得到 $16,24,32,40,48,\dots$ ，有 $(2n+2)4(n-2)(n+1)=2(2n+2{)}^2(n-2)=8(n^2-n-2)$ 即为所求。猜测后续可能需要拉格朗日插值把系数插出来。

    对于 $m=4$ 的情况，猜测含有因式 $(2n+2{)}^3$ ，得到其他部分为 $2(n-3)$ 。大致形式能进行因式分解，拉格朗日插值没什么意义了。

    大胆猜测 $2(2n+2{)}^{m-1}(n-m+1)$ 即为所求。验证后续数据及大样例发现能过。

  • 将链连接成环，在 $1$ 和 $n$ 之间用 $n+1$ 相连，此时的操作为每次选择一个点并选择是顺时针走还是逆时针走，要求不能走到 $n+1$ 。

  • 考虑统计概率，不妨认为在 $n+1$ 开始也是合法的，同时每个点被选中时相互独立，所以不在第一个点经过 $n+1$ 的概率为 $\frac{n+1-m}{n+1}$ 。故 $(2n+2{)}^m\frac{n+1-m}{n+1}=2^m(n+1{)}^m(n-m+1)$ 即为所求，与我们打表得到的式子一致。

  点击查看代码

  const ll p=998244353;
  ll qpow(ll a,ll b,ll p)
  {
      ll ans=1;
      while(b)
      {
          if(b&1)  ans=ans*a%p;
          b>>=1;
          a=a*a%p;
      }
      return ans;
  }
  int main()
  {
  #define Isaac
  #ifdef Isaac
      freopen("postbox.in","r",stdin);
      freopen("postbox.out","w",stdout);
  #endif
      ll n,m;
      cin>>n>>m;
      cout<<2*qpow(2*(n+1)%p,m-1,p)%p*((n-m+1)%p)%p<<endl;
      return 0;
  }
  

$T2$ HZTG5882. 饺子 $20pts$

• 部分分

  • 随机 $pts$ ：乱搞。
  点击查看代码

  pair<ll,ll>a[300010];
  vector<ll>pos[300010];
  int main()
  {
  #define Isaac
  #ifdef Isaac
      freopen("zongzi.in","r",stdin);
      freopen("zongzi.out","w",stdout);
  #endif
      ll n,sum,i,j;
      scanf("%lld",&n);
      for(i=1;i<=2*n-1;i++)
      {
          scanf("%lld",&a[i].first);  a[i].second=i;
          pos[a[i].first].push_back(i);
      }
      for(i=0;i<=n-1;i++)
      {
          if(pos[i].size()>=n)
          {
              for(j=0;j<=n-1;j++)  printf("%lld ",pos[i][j]);
              printf("\n");
              return 0;
          }
      }
      for(j=1;j<=4000;j++)
      {
          random_shuffle(a+1,a+1+2*n-1);
          sum=0;
          for(i=1;i<=n;i++)  sum+=a[i].first;
          if(sum%n==0)
          {
              for(i=1;i<=n;i++)  printf("%lld ",a[i].second);
              printf("\n");
              return 0;
          }
          sum=0;
          for(i=n;i<=2*n-1;i++)  sum+=a[i].first;
          if(sum%n==0)
          {
              for(i=n;i<=2*n-1;i++)  printf("%lld ",a[i].second);
              printf("\n");
              return 0;
          }
      }
      printf("-1\n");
      return 0;
  }
  

• 正解

  • 在题目的限制条件下，任意 $n-1$ 个 非 $0$ 数字的子集合取遍模 $n$ 的完全剩余系。证明考虑扩展时一旦出现扩展失败说明已经是取遍模 $n$ 的完全剩余系了，否则每次至少扩展 $1$ 个数。
  • 先特判下众数次数 $\ge n$ 的情况。然后将所有数分成 $n-1$ 个数对和一个单独的数，不妨钦定一定选择单独的数，然后决定每个数对内部选择哪个数即可。
  • 先将较小的数选择了，然后考虑调整/替换。使用 bitset 优化或树状数组维护哈希值加二分，同时记录下路径即可，写法和 2025省选模拟5 T2 HZTG5844. A Dance of Fire and Ice 差不多。
  点击查看代码

  int w[600010],vis[600010],opt[600010];
  pair<int,int>a[600010];
  vector<int>pos[600010];
  bitset<600010>f,g,tmp;
  int main()
  {
  #define Isaac
  #ifdef Isaac
      freopen("zongzi.in","r",stdin);
      freopen("zongzi.out","w",stdout);
  #endif
      int n,m,sum=0,i,j;
      cin>>n;  m=2*n-1;
      for(i=1;i<=m;i++)
      {
          cin>>a[i].first;  a[i].second=i;
          pos[a[i].first].push_back(i);
      }
      for(i=0;i<=n-1;i++)
      {
          if(pos[i].size()>=n)
          {
              for(j=0;j<=n-1;j++)  cout<<pos[i][j]<<" ";
              return 0;
          }
      }
      sort(a+1,a+1+m);  sum=a[m].first;
      for(i=1;i<=n-1;i++)  
      {
          sum=(sum+a[i].first)%n;
          w[i]=a[i+n-1].first-a[i].first;
      }
      if(sum==0)
      {
          for(i=1;i<=n-1;i++)  cout<<a[i].second<<" ";
          cout<<a[m].second<<endl;
      }
      else
      {
          sum=(n-sum)%n;  vis[a[m].second]=1;
          for(i=1;i<=n-1;i++)  vis[a[i].second]=1;
          f[0]=1;
          for(i=1;i<=n-1;i++)
          {
              g=f;
              f|=(f<<(w[i]))|(f>>(n-w[i]));
              tmp=f^g;
              for(j=tmp._Find_first();j<=n-1;j=tmp._Find_next(j))  opt[j]=i;
              if(f[sum]==1)
              {
                  for(;sum!=0;sum=(sum+n-w[opt[sum]])%n)
                      swap(vis[a[opt[sum]].second],vis[a[opt[sum]+n-1].second]);
                  for(j=1;j<=m;j++)  if(vis[j]==1)  cout<<j<<" ";
                  break;
              }
          }
      }
      return 0;
  }
  

  

$T3$ HZTG5883. 机关 $0pts$

• 拼尽全力，无法战胜。

  

  

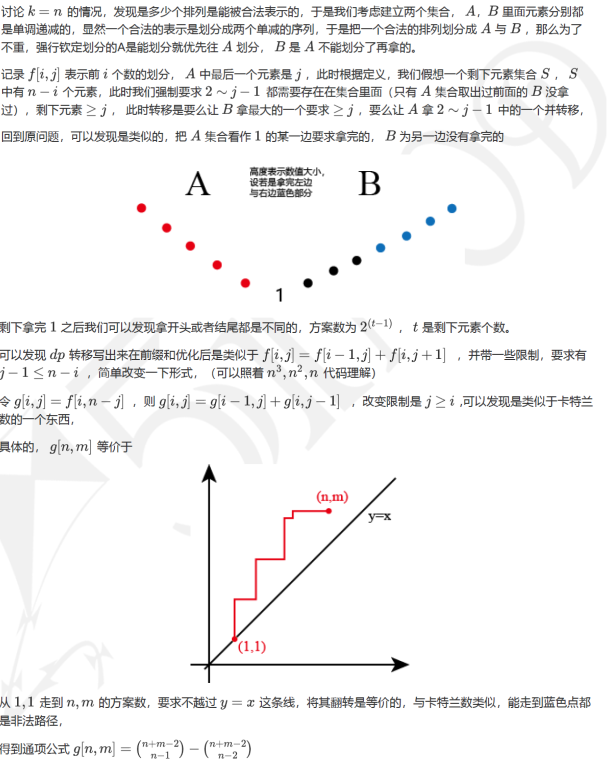
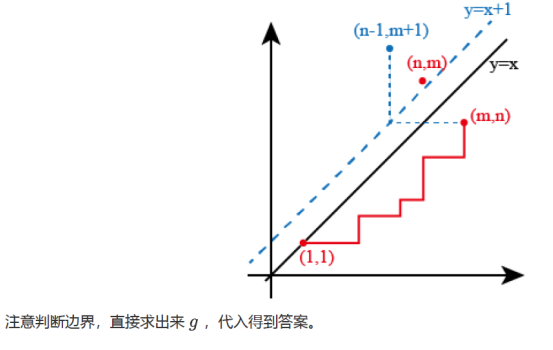
  点击查看代码

  ll qpow(ll a,ll b,ll p)
  {
      ll ans=1;
      while(b)
      {
          if(b&1)  ans=ans*a%p;
          b>>=1;
          a=a*a%p;
      }
      return ans;
  }
  ll C(ll n,ll m,ll p)
  {
      if(n>=m&&n>=0&&m>=0)
      {
          ll up=1,down=1;
          for(ll i=n-m+1;i<=n;i++)  up=up*i%p;
          for(ll i=1;i<=m;i++)  down=down*i%p;
          return up*qpow(down,p-2,p)%p;
      }
      else  return 0;
  }
  int main()
  {
  #define Isaac
  #ifdef Isaac
      freopen("game.in","r",stdin);
      freopen("game.out","w",stdout);
  #endif
      ll n,k,p;
      cin>>n>>k>>p;
      cout<<(C(n+k-3,n-2,p)-C(n+k-3,n,p)+p)%p*qpow(2,max(0ll,n-k-1),p)%p<<endl;
      return 0;
  }
  

总结

• $T1$ 在 $9:30$ 左右打完表测样例时发现 qpow(2*(n+1),m-1,p) 传进去后 2*(n+1) 炸 long long 了，改了之后就交了。在 $11:57$ 的时候发现后面 (n-m+1) 相乘时也炸 long long 了，改完后马上交了。

• $T2$ 赛时下发了 $checker$ 。

  点击查看代码

  #include "testlib.h"
  #include <bits/stdc++.h>
  
  using namespace std;
  
  const int N = 6e5 + 10;
  
  int n;
  int a[N];
  int x[N];
  
  int main(int argc, char** argv) {
      registerTestlibCmd(argc, argv);
      n = inf.readInt();
      for (int i = 1; i <= 2 * n - 1; ++i) {
          a[i] = inf.readInt();
      }
      int sum = 0;
      for (int i = 1; i <= n; ++i) {
          x[i] = ouf.readInt();
          sum = (sum + a[x[i]]) % n;
      }
      if (sum) {
          quitf(_wa, "yiw?/kk");
      }
      sort(x + 1, x + n + 1);
      for (int i = 1; i <= n; ++i) {
          if (x[i] == x[i - 1]) {
              quitf(_wa, "/qd");
          }
          if (x[i] < 1 || x[i] > 2 * n - 1) quitf(_wa, "/cf");
      }
      quitf(_ok, "AC");
      return 0;
  }
  

• $T3$ 一开始读成问有多少个合法的生成操作序列了。