2019牛客暑期多校训练营（第一场） 补题

A.Equivalent Prefixes

题意：给定两个含n个元素的数组a,b，数组中不含相同元素，求最大的p（p<=n），使得a和b等价，这里等价的定义为a[l,r]和b[l,r]的最小值下标相等（1<=l<=r<=p）。

题解：

1、p的范围是1~n，从小到大遍历，利用单调栈求出La[i]，表示第一个比a[i]小的元素的下标，Lb[i]同理。对第i个元素来说，如果Lu[i]!=Lv[i]，说明包含i在内的区间不满足上述条件，那么p最大只能取i-1。

单调栈

AC代码：

#include<iostream>
#include<sstream>
#include<fstream>
#include<algorithm>
#include<string>
#include<cstring>
#include<iomanip>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<map>
#include<set>
#define mem(a,b) memset(a,b,sizeof(a))
#define random(a,b) (rand()%(b-a+1)+a)
#define ull unsigned long long
#define e 2.71828182
#define Pi acos(-1.0)
using namespace std;
const int MAXN=1e5+5;
int n,a[MAXN],b[MAXN];
int La[MAXN],Lb[MAXN]; 
stack<int> sa,sb;
int read()
{
    int s=1,x=0;
    char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
    while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
    return x*s;
}
void init()
{
    while(!sa.empty()) sa.pop();
    while(!sb.empty()) sb.pop();
    for(int i=1;i<=n;++i)
    {
        while(!sa.empty()&&a[i]<a[sa.top()]) sa.pop();
        if(sa.empty()) La[i]=0;
        else La[i]=sa.top();
        sa.push(i);
    }
    for(int i=1;i<=n;++i)
    {
        while(!sb.empty()&&b[i]<b[sb.top()]) sb.pop();
        if(sb.empty()) Lb[i]=0;
        else Lb[i]=sb.top();
        sb.push(i);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    while(~scanf("%d",&n))
    {
        getchar();
        for(int i=1;i<=n;++i) a[i]=read();
        for(int i=1;i<=n;++i) b[i]=read();
        int ans=n;
        init();
        for(int i=2;i<=n;++i)
        {
            if(La[i]!=Lb[i])
            {
                ans=i-1;
                break;
            } 
        }
        cout<<ans<<endl;
    }
}

2、参考笛卡尔树做法

 

 B.Integration

题意：已知

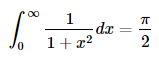
给定n个不同的数a₁,a₂,...,a_n,求值：

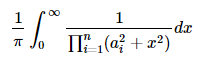
结果可以被证明是一个有理数 p/q,输出模10e9+7的值

 题解：（这是让我回炉重造再学一遍高数吗？？？）参考裂项解方程+找规律

找到的规律是

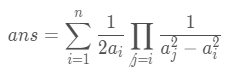
 数论做的少，这里记一下：

若整数b,p互质，并且b | a，则存在一个整数x，使得

 

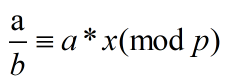
称x为b的模p乘法逆元，记为 b^-1(mod p)

因为

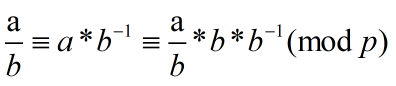
所以

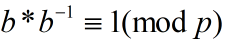
如果p是质数，并且b<p，根据费马小定理，b^p-1≡1(mod p)，即b*b^p-2≡1(mod p)。因此，当模数p为质数时，b^p-2即为b的乘法逆元。

如果只是保证b,p互质，那么乘法逆元可通过求解同余方程b*x≡1(mod p)得到。

有了乘法逆元，我们在计数问题中即使遇到a/b这样的除法算式，也可以先把a, b各自对模数p取模，再计算a*b^-1 mod p作为最终的结果。当然，前提是必须保证b，p互质（当p时质数时，等价于b不是p的倍数）。

AC代码：

#include<iostream>
#include<sstream>
#include<fstream>
#include<algorithm>
#include<cstring>
#include<iomanip>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<string>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<map>
#include<set>
#define mem(a,b) memset(a,b,sizeof(a))
#define random(a,b) (rand()%(b-a+1)+a)
#define ll long long
#define ull unsigned long long
#define e 2.71828182
#define Pi acos(-1.0)
using namespace std;
const int MOD=1e9+7;
const int MAXN=1e3+5;
ll qp(ll x,ll n)
{
    ll ans=1;
    while(n)
    {
        if(n&1) ans=ans*x%MOD;
        x=x*x%MOD;
        n>>=1;
    }
    return ans;
}
ll a[MAXN];
int n;
int read()
{
    int s=1,x=0;
    char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
    while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
    return x*s;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    while(~scanf("%d",&n))
    {
        for(int i=1;i<=n;++i) a[i]=read();
        ll ans=0;
        for(int i=1;i<=n;++i)
        {
            ll tmp=1;
            for(int j=1;j<=n;++j)
            {
                if(i==j) continue;
                tmp=tmp*((a[j]*a[j]%MOD-a[i]*a[i]%MOD+MOD)%MOD)%MOD;
            }
            tmp=tmp*2%MOD*a[i]%MOD;
            ans=(ans+qp(tmp,MOD-2))%MOD;
        }
        cout<<ans<<endl;
    }
}

 

C.Euclidean Distance

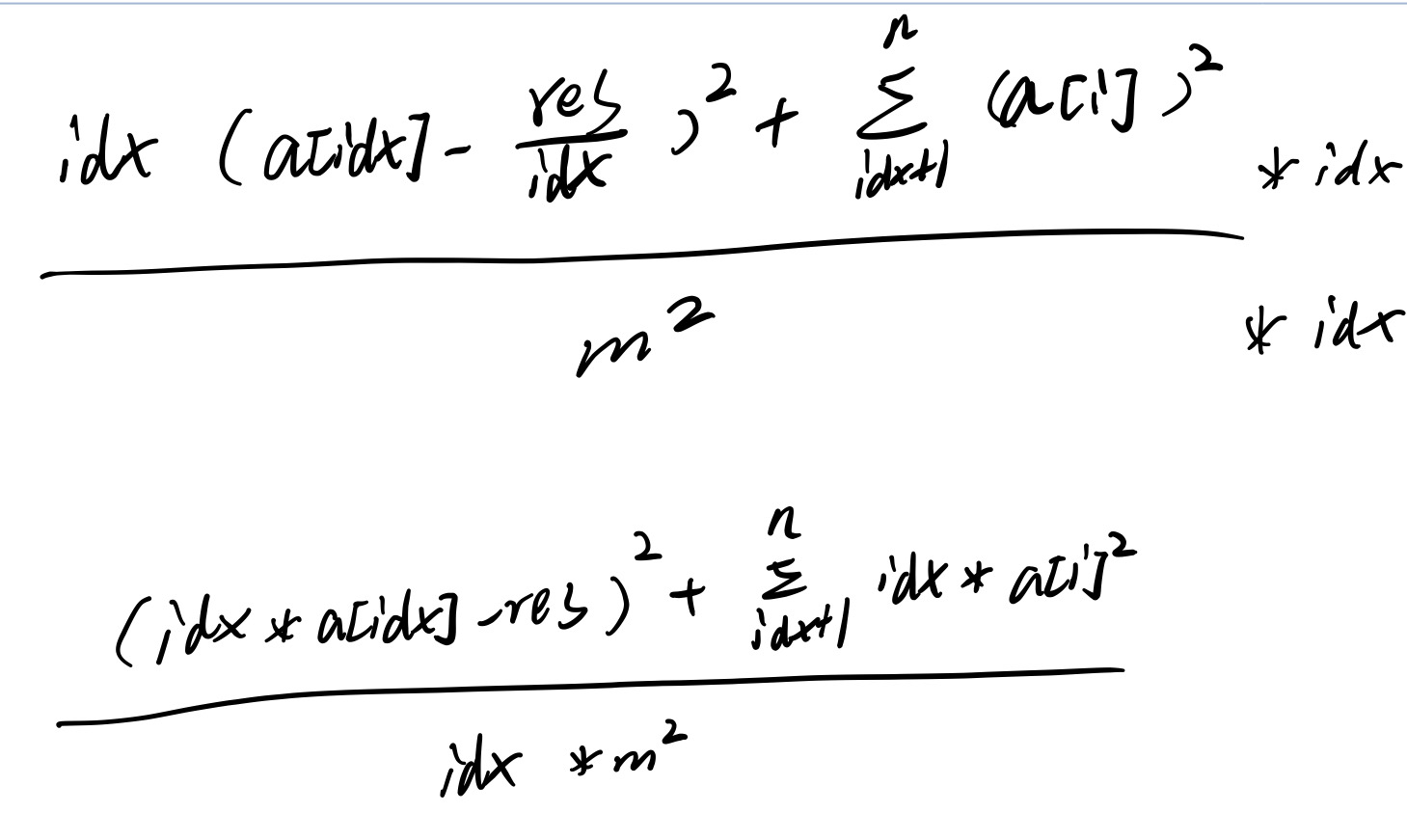
题意：给定n个数字a₁到a_n，求n个实数p₁到p_n使得∑(a_i/m-p_i)² 最小，并且满足p₁+p₂+...+p_n=1, p₁,p₂,...,p_n>=0。输出最简分数。

题解：参考2019牛客暑期多校1C题 （数形结合好评）

a_i是独立的，先排序，敢想，勇于贪心！也可以先想想n=2、3的情况，勇于贪心！

AC代码：

#include<iostream>
#include<sstream>
#include<fstream>
#include<algorithm>
#include<cstring>
#include<iomanip>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<string>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<map>
#include<set>
#define mem(a,b) memset(a,b,sizeof(a))
#define random(a,b) (rand()%(b-a+1)+a)
#define ll long long
#define ull unsigned long long
#define e 2.71828182
#define Pi acos(-1.0)
using namespace std;
const int MAXN=1e4+5;
int read()
{
    int s=1,x=0;
    char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
    while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
    return x*s;
}
int n,m;
ll a[MAXN];
void solve()
{
    for(int i=1;i<=n;++i) a[i]=read();
    sort(a+1,a+n+1,greater<int>());
    int idx=n,res=m,tmp;
    for(int i=1;i<n;++i)
    {
        if(i*(a[i]-a[i+1])<=res)
        res-=i*(a[i]-a[i+1]);
        else 
        {
            idx=i;break;
        }
    }
    ll fz=(idx*a[idx]-res)*(idx*a[idx]-res);
    for(int i=idx+1;i<=n;++i)
    fz+=idx*a[i]*a[i];
    ll fm=idx*m*m;
    tmp=__gcd(fz,fm);
    fz/=tmp,fm/=tmp;
    if(!fz||fm==1) cout<<fz<<endl;
    else cout<<fz<<'/'<<fm<<endl;
}
int main()
{
    /*ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);*/
    while(~scanf("%d%d",&n,&m))
    {
        solve();
    }
    return 0;
}

 

D.Parity of Tuples

题意：给定n 个m维向量，定义count(x)为满足条件的向量个数，满足的条件为：向量v_i中的每一个数a_i,j与x按位与后的二进制表示中要有奇数个1，1<=i<=n,1<=j<=m。

求

参考：2019多校第一场DParity of Tuples

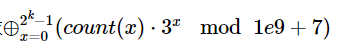
告辞！

 

 E.ABBA

题意：

 构造一个长度为2*(m+n)的字符串，使得有一种子序列能拆分出n个AB及m个BA，求方案数。

题解：

2019牛客暑期多校训练（第一场）E-ABBA（卡特兰数的扩展）（超级无敌巨详细）

 

F.Random Point in Triangle

题意：给定三角形的三个点A(x1,y1)，B(x2,y2)，C(x3,y3)，在三角形上找一点P，设E=max{S_ABP,S_BCP,S_ACP}，求E的期望

题解：参考：2019牛客暑期多校训练营（第一场）F.Random Point in Triangle(几何概型积分求期望)

答案是22倍三角形的面积

import java.util.*;
import java.io.*;
public class Main {
 
    public static void main(String[] args) {
        Scanner cin=new Scanner(new BufferedInputStream(System.in));
        long x1,x2,x3,y1,y2,y3;
        while(cin.hasNext())
        {
            x1=cin.nextLong();y1=cin.nextLong();
            x2=cin.nextLong();y2=cin.nextLong();
            x3=cin.nextLong();y3=cin.nextLong();
            System.out.println(Math.abs(x2*y3+x1*y2+x3*y1-x1*y3-x3*y2-x2*y1)*11);
        }
         
        cin.close();
 
    }
 
}

 

G.Substrings 2

 

H.XOR

 

I.Points Division

 

J.Fraction Comparision

(签到题，略）