3.2324物理强基小记

物理强基课

• 有人听强基课是听提高，有人听强基课是听水题，有人听强基课是听新课，怎么回事呢？

弹簧

类SHM

• SHM 中，都可以规约成 \(E_p=\dfrac{1}{2}kx^2,E_k=\dfrac{1}{2}mv^2\)

例1

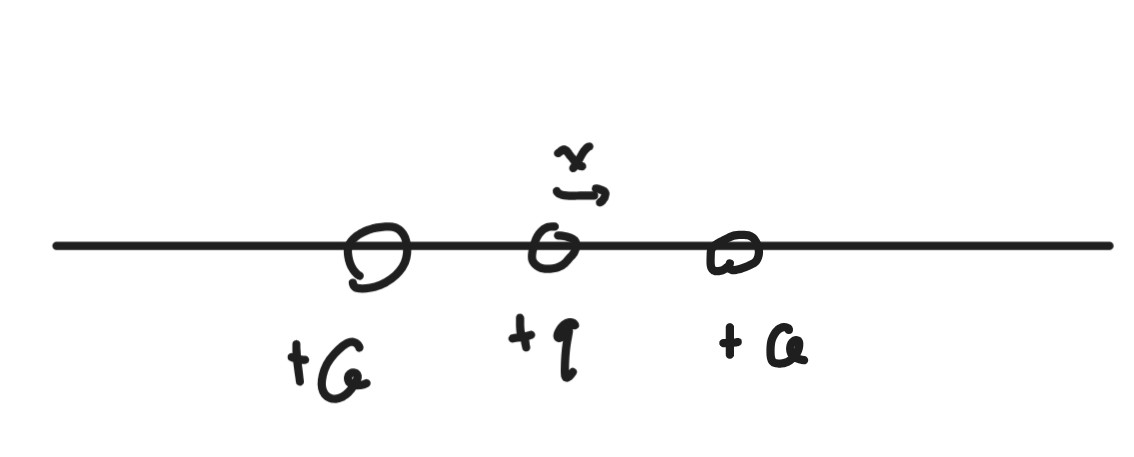
\(Q\) 固定，\(q\) 穿在绝缘光滑杆，总长 \(l\)，一个小移动 \(x\)，\(x<<l\)

• Trick：\((1+x)^n=1+nx(x<<1)\)

\[\begin{aligned} F&=k\dfrac{Qq}{(l/2+x)^2}-k\dfrac{Qq}{(l/2-x)^2}\\ &=\dfrac{kQq}{(l/2)^2}((1+2x/l)^{-2}-(1-2x/l)^{-2})\\ &=-\dfrac{4kQq}{l^2}\dfrac{8x}{l}=-\dfrac{32kQqx}{l^3}\\ &=-kx\\ k&=\dfrac{32kQq}{l^3} \end{aligned} \]

例2

\[\begin{aligned} E_p-0&=-W_t\\ F_h&=mg-k(s+x_0)=-kx_0 \end{aligned} \]

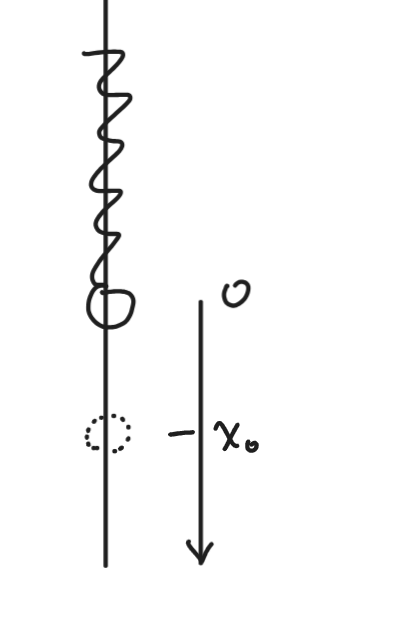
例3

原长为势能 \(0\) 点，一个小的变化量 \(x\)

\[\begin{aligned} 0+0+0&=mgx\sin\theta+(-2mgx)+\dfrac{1}{2}kx^2+\dfrac{1}{2}(3m)v^2\\ \dfrac{3}{2}mv^2+\dfrac{1}{2}kx^2-\dfrac{3}{2}mgx&=0\\ \dfrac{3}{2}mv^2+\dfrac{1}{2}k(x-\dfrac{3mg}{2k})^2&=\dfrac{(3mg)^2}{8k} \end{aligned} \]

类简谐运动？配方高妙

蹦极类型

从初中就开始学习了，加上一些图像让做题更简单（复杂）

\(a-x\) 图像

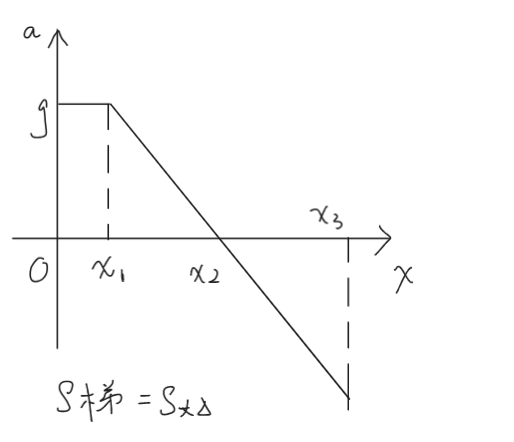
图片少了个 \(a_m\)，为 \(x_3\) 对应的纵坐标

\(v:\dfrac{v^2}{2}-0=\dfrac{1}{2}(x_1+x_2)g\)

\(a_m:\dfrac{a_m}{g}=\sqrt{\dfrac{S_b}{S_s}}=\sqrt{\dfrac{\dfrac{1}{2}(x_1+x_2)g}{\dfrac{1}{2}(x_2-x_1)g}}=\sqrt{\dfrac{x_1+x_2}{x_2-x_1}}\)

\(x_3:\dfrac{1}{2}(x_1+x_2)g=\dfrac{1}{2}(x_3-x_2)a_m\)

\(x_3:mg=k(x2-x1),mgx_3=\dfrac{1}{2}k(x_3-x_1)^2\)

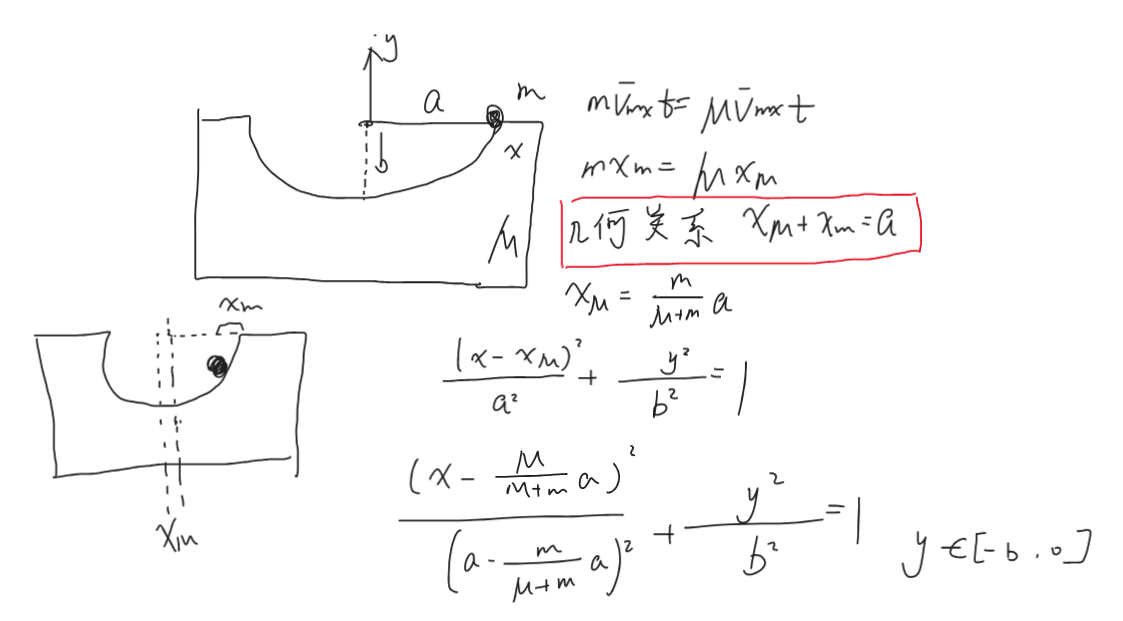
两体模型

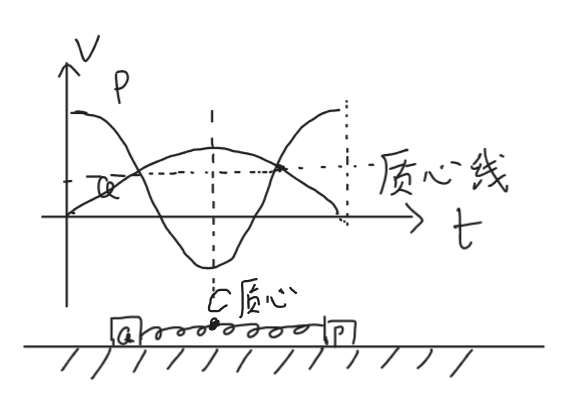
给 \(P\) 一个向左的速度 \(v_0\)，

\[\begin{aligned} r_c&=\dfrac{m_pr_p+m_qr_q}{m_p+m_q}\\ v_c&=\dfrac{m_pv_p+m_qv_q}{m_p+m_q}\\ a_c&=\dfrac{m_pa_p+m_qa_q}{m_p+m_q} \end{aligned} \]

其中 \(r,v,a\) 均为向量，有方向

\(P,Q\) 相对质心动量等大反向，整个过程中质心的速度不变

力学综合

微量移动证明

电荷量 \(Q\)，半径为 \(R\)，球壳表面的电荷之间将相互排斥；已知此带电球壳体系储存的静电能为 \(E=k\dfrac{Q^2}{2R}\)，求球壳单位面积上受到的排斥力

\[\begin{aligned} f\Delta s\Delta R&=-(\dfrac{kQ^2}{2(R+\Delta R)}-\dfrac{kQ^2}{2R})\\ f4\pi R^2\Delta R&=\dfrac{kQ^2}{2R}-\dfrac{kQ^2}{2R}(1+\dfrac{\Delta R}{R})^{-1}\\ f&=\dfrac{kQ^2}{8\pi R^4} \end{aligned} \]

运动轨迹

电场

一些基础的公式

单电子产生的球壳电场

电场的叠加是向量，电势的叠加是代数的叠加

例1

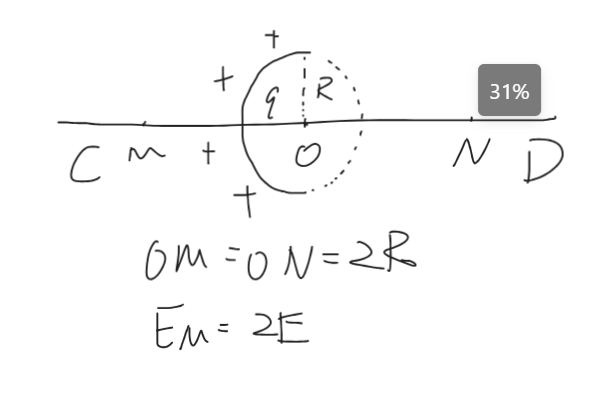
//什么情况怎么把缩放带上了

补全法处理

1.求 \(N\) 点电场

\(E_M+E_{M'}=E_U=\dfrac{k(2q)}{OM^2}\)

\(E_N=E_{M'}=E_U-E_M=\dfrac{k(2q)}{4R^2}-2E=\dfrac{kq}{2R^2}-2E\)

2.已知 \(\varphi_M\)，求 \(\varphi_N\)

\(\varphi_M+\varphi_{M'}=\dfrac{k(2q)}{OM}=\dfrac{kq}{R}\)

周期性问题

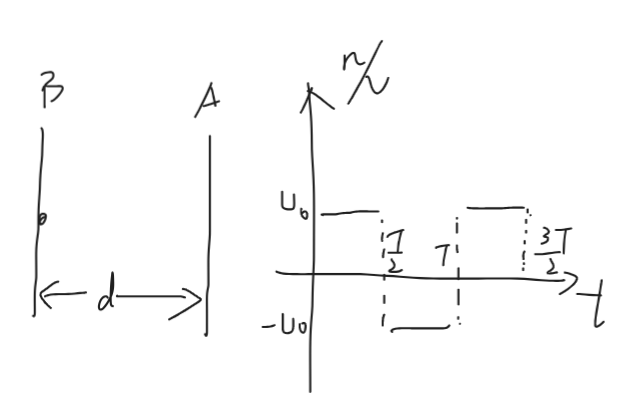
交变电压频率逐渐变大

\[\begin{aligned} E=\dfrac{U_0}{d}\\ a=\dfrac{qE}{m}\\ d=\dfrac{1}{2}at^2 d=\dfrac{1}{2}\dfrac{qU_0}{md}(\dfrac{1}{2f})^2(2n+1)\\ d=(2n)\dfrac{1}{2}\dfrac{qU_0}{md}(\dfrac{1}{2f})^2 \end{aligned} \]

等效重力场

给了一堆题自己看