题解 P4536 [CQOI2007]三角形

原题

本题是一道找规律模拟的题目，做法有很多，找到规律后就不难。

看到很多题解都是反着推的，这里写一篇正推的题解。

题意

首先题面就有点晦涩难懂，题目建立在一个三角形的不断分割之中，这个看了图后是比较好理解的，题目中定义三角形所靠着的三角形为：

• 如果 B 不包含 A，且 A 的某一条完整的边是 B 的某条边的一部分，则我们说 A 靠在 B 的边上。

配合这张图就比较好理解了。

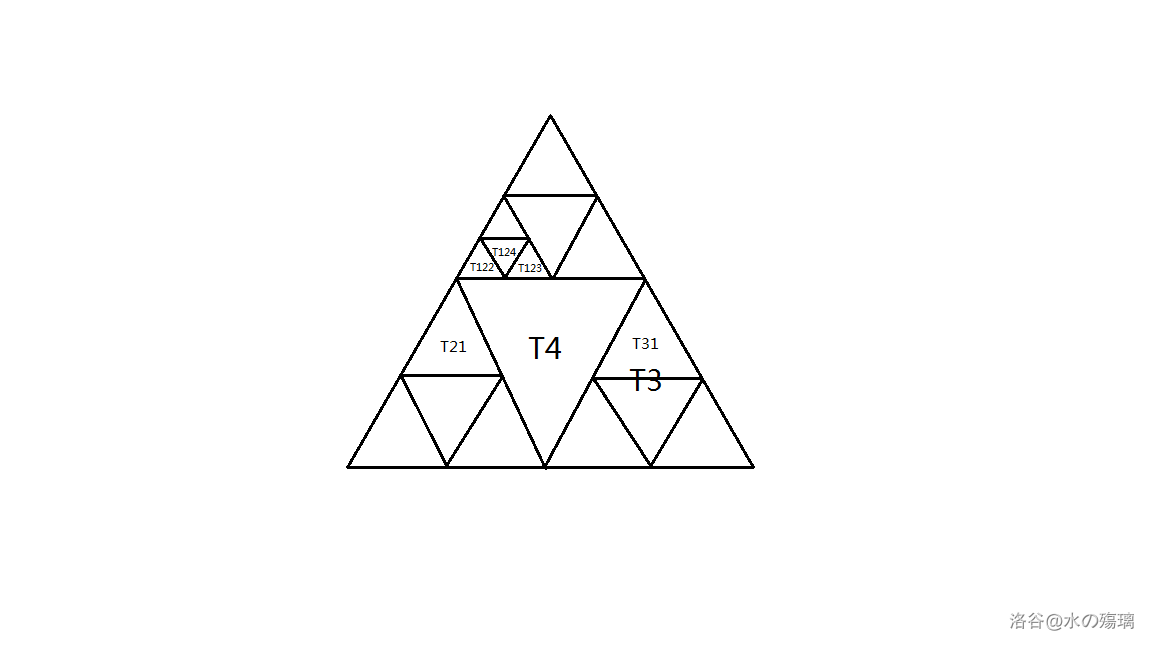
如图，对于 $\triangle\texttt{T122}$，它与 $\triangle\texttt{T124}$ 和 $\triangle\texttt{T4}$ 相邻，但它不与 $\triangle\texttt{T123}$ 和 $\triangle\texttt{T21}$ 相邻。

对于 $\triangle\texttt{T31}$，虽然它有边是 $\triangle\texttt{T3}$ 的边的一部分，但因为 $\triangle\texttt{T3}$ 包含 $\triangle\texttt{T31}$，所以 $\triangle\texttt{T31}$ 不与 $\triangle\texttt{T3}$ 相邻。

至于每个三角形的编号，大概是递归式的，每一个字符代表着四个部分中的一个，其中4表示中间的三角形，显然只可能出现在末位，然后下一个字符就继续分四个部分。

到这里，题意已经很明确了。

思路

$S$ 表示三角形编号的字符串，$len$ 表示字符串 $S$ 的长度，观察后我们发现该分形有以下性质：

1. 若 $\triangle S$ 与 $\triangle S'$ 不相邻，$t$ 表示该三角形编号的一段后缀字符串，则 $\triangle S+t$ 和 $\triangle S'$ 不相邻。
2. 若 $S_{len}=4$，则该三角形相邻的三角形仅为 $S_{len} \in \{1,2,3\}$ 时的 $\triangle S$。
3. 若 $S_{len}\neq4$，则该三角形必有一个三角形为 $S_{len}=4$ 时的 $\triangle S$ 与之相邻，且所有与该三角形相邻的三角形序号最后一个字符都为 $4$。
4. 若 $\triangle S_{len}\in\{1,2,3\}$ 且 $S_{len-i} = S_{len}\ (i \in \left[1,len-1\right])$，令 $S'$ 为 $S_1$ 至 $S_{len-i-1}$ 组成的字符串且 $S'_{len-i}= 4$，则 $\triangle S$ 与 $\triangle S'$ 不相邻。

有了以上性质，我们可以得出以下结论：

• 若给定的三角形编号末位字符为 $4$，根据性质 $2$，显然能求出与该三角形相邻的所有三角形。
• 若给定的三角形编号末位字符不为 $4$，循环遍历每一个字符，根据性质 $3$，每次均插入同级的中央三角形，再根据性质 $4$，还需要把已不相邻的三角形删除，其正确性可以通过性质 $1$ 证明。

上述思路貌似很复杂，但只要多画图，多找规律，其实也是很容易理解的。

接下来顺着结论模拟即可，我们扫了一遍字符串，每一个字符还要往回扫一遍删除，加上最后的排序，时间复杂度为 $O(n^2+n\log n)$。

奉上代码。

#include <bits/stdc++.h>
using namespace std;
string s , t;
int n;
vector <string> ans;
void solve() {
    if(s[n] == '4') {//特判末位为4 
        t = s.substr(0 , n + 1); 
        t[n] = '1';
        ans.push_back(t);
        t[n] = '2';
        ans.push_back(t);
        t[n] = '3';
        ans.push_back(t);
        cout << ans[0] << "\n" << ans[1] << "\n" << ans[2] << "\n";
        return;
    }
    if(n == 1) {//因为后面从2开始循环，所以要特判1 
        cout << "T4" << "\n";
        return;
    }
    ans.push_back("T4");//初始时T4是相邻的，要先插入 
    for(int i = 2; i <= n; i ++) {
        for(int j = 1; j <= i - 1; j ++)    
            if(s[i - j] == s[i])//如上述性质4，删除已不相邻的三角形 
                for(int k = 0; k < ans.size(); k ++) 
                    if(ans[k][i - j] == '4') //末位为4即为该级的中央三角形 
                        ans.erase(ans.begin() + k);
        t = s.substr(0 , i + 1);
        t[i] = '4'; 
        ans.push_back(t);
        t[i] = s[i];
    }
    sort(ans.begin() , ans.end());//按字典序排序 
    for(int i = 0; i < ans.size(); i ++) 
        cout << ans[i] << "\n";
}
int main() {
    ios::sync_with_stdio(false);
    cin >> s;
    n = s.size() - 1;
    solve();
    return 0;
}