题解 CF803G Periodic RMQ Problem

$\texttt{link}$

题意

给定一个长度为 $n$ 的序列 $b_{1\dots n}$，将其首尾相接 $k$ 次得到序列 $a_{1\dots nk}$，在 $a$ 上进行 $q$ 次操作：

• 区间推平
• 区间查询最小值

数据范围：$1\le n,q\le 10^5$，$1\le k\le10^4$，$1\le b_i\le10^9$

题解

又是一道 DS 妙题。

$a$ 的长度能到 $10^9$，用朴素线段树做时间复杂度 $O(nk\log nk)$，空间也到了 $O(nk)$，显然不能接受。

空间可以动态开点优化至 $O(q\log nk)$，这个结构看上去就很可以用动态开点线段树做。

发现每次新建节点都要求出区间的最小值，考虑如何快速求出。

对于一个新建的节点，该区间是由 $b$ 构成的，考虑将该区间的最小值转化到序列 $b$ 上。

设区间为 $\left[l,r\right]$，便于处理，这里下标从 $0$ 开始，分三类讨论：

1. 当 $r-l+1\ge n$ 时，此时一定包含了整个 $b$ 序列，区间最小值为 $\min\limits_{i=0}^{n-1}b_i$。

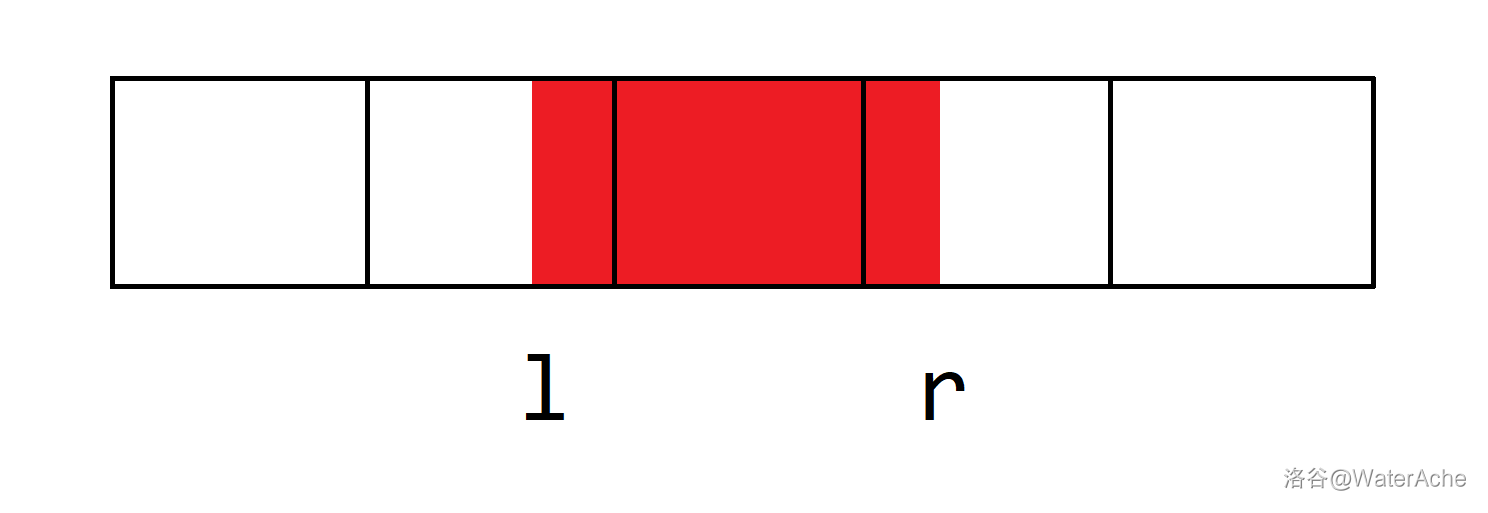
2. 当 $r-l+1<n$ 且 $\lfloor\frac{l}{n}\rfloor=\lfloor\frac{r}{n}\rfloor$ 时，$l,r$ 在同一 $b$ 序列中，区间最小值为 $\min\limits_{i=l\bmod n}^{r\bmod n}b_i$。

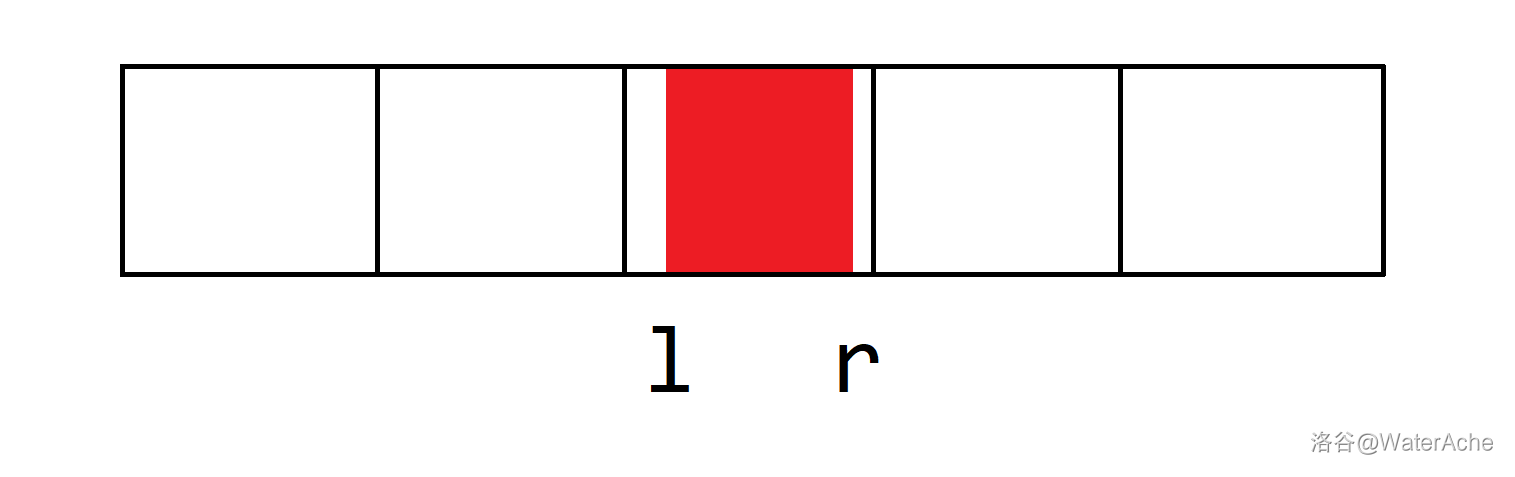
3. 当 $r-l+1<n$ 且 $\lfloor\frac{l}{n}\rfloor\ne\lfloor\frac{r}{n}\rfloor$ 时，$l,r$ 恰分布在两个 $b$ 序列中的连续段，区间最小值为 $\min(\min\limits_{i=l\bmod n}^{n-1}b_i,\min\limits_{i=0}^{r\bmod n}b_i)$。

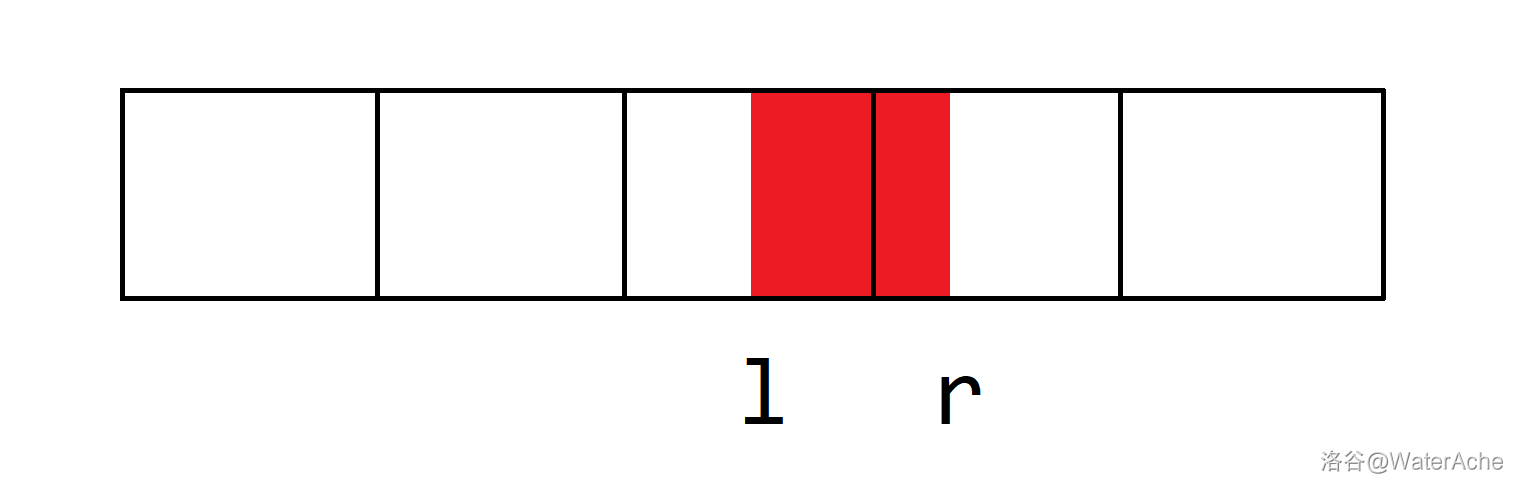
于是可以对 $b$ 开一个 ST 表维护区间最小值做到 $O(1)$ 开点，总时间复杂度为 $O(q\log nk)$。

感觉写下来有种分块的味道，整体还算小清新。

顺便提一嘴数组开的大小，因为下传标记时会开左右儿子的点，所以实际上还有一个常数 $2$，数组大小为 $2\times10^5\times\log(10^9)\approx6\times10^6$。

#include <bits/stdc++.h>
using namespace std;
namespace IO {
    //read and write
} using namespace IO;
const int N = 1e5 + 10, M = 6e6 + 10, L = 20;
int n, k, q;
namespace RMQ {
    int st[L][N];
    void init() {
        for(int i = 1; (1 << i) <= n; i++)
            for(int j = 0; j + (1 << i) - 1 < n; j++)
                st[i][j] = min(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
    }
    int Min(int l, int r) {
        int len = log2(r - l + 1);
        return min(st[len][l], st[len][r - (1 << len) + 1]);
    }
} using namespace RMQ;
namespace SegmentTree {
    int rt, ls[M], rs[M], mn[M], tag[M], cnt;
    int newnode(int l, int r) {
        ++cnt;
        if(r - l + 1 >= n) return mn[cnt] = Min(0, n - 1), cnt;
        if(l / n == r / n) return mn[cnt] = Min(l % n, r % n), cnt;
        return mn[cnt] = min(Min(l % n, n - 1), Min(0, r % n)), cnt;
    }
    void pushup(int x) { mn[x] = min(mn[ls[x]], mn[rs[x]]); }
    void pushdown(int x, int l, int r) {
        int mid = l + r >> 1;
        if(!ls[x]) ls[x] = newnode(l, mid);
        if(!rs[x]) rs[x] = newnode(mid + 1, r);
        if(!tag[x]) return;
        mn[ls[x]] = mn[rs[x]] = tag[ls[x]] = tag[rs[x]] = tag[x];
        tag[x] = 0;
        return;
    }
    void modify(int &x, int l, int r, int L, int R, int v) {
        if(!x) x = newnode(l, r);
        if(L <= l && r <= R) { mn[x] = tag[x] = v; return; };
        pushdown(x, l, r);
        int mid = l + r >> 1;
        if(mid >= L) modify(ls[x], l, mid, L, R, v);
        if(mid < R) modify(rs[x], mid + 1, r, L, R, v);
        pushup(x); 
    }
    int query(int &x, int l, int r, int L, int R) {
        if(!x) x = newnode(l, r);
        if(L <= l && r <= R) return mn[x];
        pushdown(x, l, r);
        int mid = l + r >> 1, res = 2e9;
        if(mid >= L) res = min(res, query(ls[x], l, mid, L, R));
        if(mid < R) res = min(res, query(rs[x], mid + 1, r, L, R));
        return res;
    }
} using namespace SegmentTree;
int main() {
    n = read(), k = read();
    for(int i = 0; i < n; i++) st[0][i] = read();
    init();
    q = read();
    int opt, l, r, x;
    while(q--) {
        opt = read(), l = read() - 1, r = read() - 1;
        if(opt == 1) x = read(), modify(rt, 0, n * k - 1, l, r, x);
        else write(query(rt, 0, n * k - 1, l, r)), putc('\n');
    }
    flush();
    return 0;
}