二维平面上判断点是否在三角形内
最近在项目中碰到的这个问题,在此记录一下。已知三角形的三个顶点坐标,判断某个点是否在三角形中(在三角形的边上,我们也视作在三角形中),本文给出了三种方法。
算法1
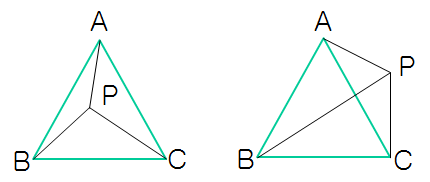
利用面积法,如上图所示,如果点P在三角形ABC的内部,则三个小三角形PAB, PBC, PAC的面积之和 = ABC的面积,反之则不相等。
已知三角形的三个顶点坐标求其面积,可以根据向量的叉乘,参考here。
该算法详见后面代码中的函数:IsPointInTriangle1
算法2
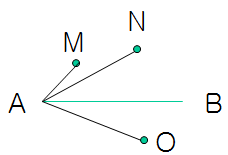
首先看一下这个问题,如何判断某两个点在某条直线的同一侧(代码中函数:IsPointAtSameSideOfLine)?
根据向量的叉乘以及右手螺旋定则,AB^AM (^表示叉乘,这里向量省略了字母上面的箭头符号)的方向为向外指出屏幕,AB^AN也是向外指出屏幕,但AB^AO的方向是向内指向屏幕,因此M,N在直线AB的同侧,M ,O在直线AB的两侧。实际计算时,只需要考虑叉积的数值正负
假设以上各点坐标为A(0,0), B(4,0), M(1,2), N(3,4), O(3,-4), 则:
AB^AM = (4,0)^(1,2) = 4*2 - 0*1 = 8
AB^AN = (4,0)^(3,4) = 4*4 – 0*3 = 16
AB^AO = (4,0)^(3,-4) = 4*-4 – 0*3 = –16
由上面的数值可知,可以根据数值的正负判断叉乘后向量的方向。即,如果叉积AB^AM 和 AB^AN的结果同号,那么M,N两点就在直线的同侧,否则不在同一侧。特殊地,如果点M在直线AB上,则AB^AM的值为0。(如果是在三维坐标系中,求出的叉积是一个向量,可以根据两个向量的点积结果正负来判断两个向量的是否指向同一侧) 本文地址
以上的问题解决了,就很容易的用来判断某个点是否在三角形内,如果P在三角形ABC内部,则满足以下三个条件:P,A在BC的同侧、P,B在AC的同侧、PC在AB的同侧。某一个不满足则表示P不在三角形内部。
该算法详见后面代码中的函数:IsPointInTriangle2
算法3
该方法也用到了向量。对于三角形ABC和一点P,可以有如下的向量表示:
p点在三角形内部的充分必要条件是:1 >= u >= 0, 1 >= v >= 0, u+v <= 1。
已知A,B,C,P四个点的坐标,可以求出u,v,把上面的式子分别点乘向量AC和向量AB
解方程得到:
解出u,v后只需要看他们是否满足“1 >= u >= 0, 1 >= v >= 0, u+v <= 1”,如满足,则,p 在三角形内。
(u = 0时,p在AB上, v = 0时,p在AC上,两者均为0时,p和A重合)
该算法详见后面代码中的函数:IsPointInTriangle3
算法4
该算法和算法2类似,可以看作是对算法2的简化,也是用到向量的叉乘。假设三角形的三个点按照顺时针(或者逆时针)顺序是A,B,C。对于某一点P,求出三个向量PA,PB,PC, 然后计算以下三个叉乘(^表示叉乘符号):
t1 = PA^PB,
t2 = PB^PC,
t3 = PC^PA,
如果t1,t2,t3同号(同正或同负),那么P在三角形内部,否则在外部。
该算法详见后面代码中的函数:IsPointInTriangle4
经过测试,算法4最快,算法3次之,接着算法2,算法1最慢。直观的从计算量上来看,也是算法4的计算量最少。
以下是代码,定义了两个类:二维向量类 和 三角形类
#include<string>
#include<sstream>
#include<fstream>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<vector>
#include<stack>
#include<queue>
#include<list>
#include<algorithm>
#include<ctime>
#include<unordered_map>
#include<map>
#include<typeinfo>
#include<cmath>
#include<ctime>
#include<climits>
using namespace std;
//类定义:二维向量
class Vector2d
{
public:
double x_;
double y_;
public:
Vector2d(double x, double y):x_(x), y_(y){}
Vector2d():x_(0), y_(0){}
//二维向量叉乘, 叉乘的结果其实是向量,方向垂直于两个向量组成的平面,这里我们只需要其大小和方向
double CrossProduct(const Vector2d vec)
{
return x_*vec.y_ - y_*vec.x_;
}
//二维向量点积
double DotProduct(const Vector2d vec)
{
return x_ * vec.x_ + y_ * vec.y_;
}
//二维向量减法
Vector2d Minus(const Vector2d vec) const
{
return Vector2d(x_ - vec.x_, y_ - vec.y_);
}
//判断点M,N是否在直线AB的同一侧
static bool IsPointAtSameSideOfLine(const Vector2d &pointM, const Vector2d &pointN,
const Vector2d &pointA, const Vector2d &pointB)
{
Vector2d AB = pointB.Minus(pointA);
Vector2d AM = pointM.Minus(pointA);
Vector2d AN = pointN.Minus(pointA);
//等于0时表示某个点在直线上
return AB.CrossProduct(AM) * AB.CrossProduct(AN) >= 0;
}
};
//三角形类
class Triangle
{
private:
Vector2d pointA_, pointB_, pointC_;
public:
Triangle(Vector2d point1, Vector2d point2, Vector2d point3)
:pointA_(point1), pointB_(point2), pointC_(point3)
{
//todo 判断三点是否共线
}
//计算三角形面积
double ComputeTriangleArea()
{
//依据两个向量的叉乘来计算,可参考http://blog.csdn.net/zxj1988/article/details/6260576
Vector2d AB = pointB_.Minus(pointA_);
Vector2d BC = pointC_.Minus(pointB_);
return fabs(AB.CrossProduct(BC) / 2.0);
}
bool IsPointInTriangle1(const Vector2d pointP)
{
double area_ABC = ComputeTriangleArea();
double area_PAB = Triangle(pointP, pointA_, pointB_).ComputeTriangleArea();
double area_PAC = Triangle(pointP, pointA_, pointC_).ComputeTriangleArea();
double area_PBC = Triangle(pointP, pointB_, pointC_).ComputeTriangleArea();
if(fabs(area_PAB + area_PBC + area_PAC - area_ABC) < 0.000001)
return true;
else return false;
}
bool IsPointInTriangle2(const Vector2d pointP)
{
return Vector2d::IsPointAtSameSideOfLine(pointP, pointA_, pointB_, pointC_) &&
Vector2d::IsPointAtSameSideOfLine(pointP, pointB_, pointA_, pointC_) &&
Vector2d::IsPointAtSameSideOfLine(pointP, pointC_, pointA_, pointB_);
}
bool IsPointInTriangle3(const Vector2d pointP)
{
Vector2d AB = pointB_.Minus(pointA_);
Vector2d AC = pointC_.Minus(pointA_);
Vector2d AP = pointP.Minus(pointA_);
double dot_ac_ac = AC.DotProduct(AC);
double dot_ac_ab = AC.DotProduct(AB);
double dot_ac_ap = AC.DotProduct(AP);
double dot_ab_ab = AB.DotProduct(AB);
double dot_ab_ap = AB.DotProduct(AP);
double tmp = 1.0 / (dot_ac_ac * dot_ab_ab - dot_ac_ab * dot_ac_ab);
double u = (dot_ab_ab * dot_ac_ap - dot_ac_ab * dot_ab_ap) * tmp;
if(u < 0 || u > 1)
return false;
double v = (dot_ac_ac * dot_ab_ap - dot_ac_ab * dot_ac_ap) * tmp;
if(v < 0 || v > 1)
return false;
return u + v <= 1;
}
bool IsPointInTriangle4(const Vector2d pointP)
{
Vector2d PA = pointA_.Minus(pointP);
Vector2d PB = pointB_.Minus(pointP);
Vector2d PC = pointC_.Minus(pointP);
double t1 = PA.CrossProduct(PB);
double t2 = PB.CrossProduct(PC);
double t3 = PC.CrossProduct(PA);
return t1*t2 >= 0 && t1*t3 >= 0;
}
};
int main()
{
Triangle tri(Vector2d(0,0), Vector2d(6,6), Vector2d(12,0));
srand(time(0));
for(int i = 0; i < 20; ++i)
{
Vector2d point((rand()*1.0 / RAND_MAX) * 12, (rand()*1.0 / RAND_MAX) * 6);
cout<<point.x_<<" "<<point.y_<<": ";
cout<<tri.IsPointInTriangle1(point)<<" ";
cout<<tri.IsPointInTriangle2(point)<<" ";
cout<<tri.IsPointInTriangle3(point)<<" ";
cout<<tri.IsPointInTriangle4(point)<<endl;
}
}
参考资料:
http://www.cnblogs.com/graphics/archive/2010/08/05/1793393.html
http://blog.csdn.net/fox64194167/article/details/8147460
http://blog.csdn.net/dracularking/article/details/2217180
【版权声明】转载请注明出处:http://www.cnblogs.com/TenosDoIt/p/4024413.html


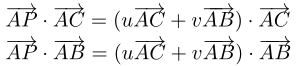
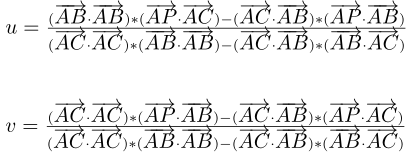

 浙公网安备 33010602011771号
浙公网安备 33010602011771号