做题随笔：P10451

Solution

注意：已被 Hack，留题解仅为请求添加 Hack 数据

仅以此题解警戒每一个数据水的题……

Hack by @yong2024

1

00001110000111110010001111

00001110001110110000011111

题意

原题链接

对每组数据，给定两颗用 01 序列描述的树，描述规则如下：

1. 按照 \(\text{DFS}\) 序进行遍历；
2. 若序列中某位为 0，表示除根节点外的节点进栈；为 1 则表示出栈。

要求判断一树是否可以通过交换子树的方式变换成另一子树（对于本题，即两树同构）。

分析

1. 朴素算法

从上述概念，自然可以得到两树 \(T_1,T_2\) 同构的必要条件：\(T_1\) 与 \(T_2\) 有且仅有以下三种关系：

1. 均为空；
2. 二者全等；
3. 交换子树后全等。

于是自然可以想到对每组数据分别建树，然后递归验证以上条件进行判断。验证部分伪代码如下：

chk(f1,f2)//f1,f2 表示当前 T1,T2 正验证的结点编号
    if son[f1]==son[f2]=∅//son[f] 表示 f 的儿子的点集
        return true;
    else if son[f1]=∅ or son[f2]=∅
        return false;
    for each x ∈ son[f1]
        for each y ∈ son[f2]
            return chk(son[f1],son[f2])

随便想想都感觉会炸，下面会介绍能过的算法。

其实判断树同构还有更好的算法，如 \(\text{AHU}\) 算法（如果学过的童靴就会发现，其实本题的输入就和暴力 \(\text{AHU}\) 的结点特征名很像）或者树哈希，可以 \(O(n)\) 或 \(O(n \log n)\) 完成。但是考虑到这只是个普及/提高-，只留链接供大家了解 AHU。

2. 针对此题的特解

根据上文的代码可以发现，由于本题点和边都没有特征，判同构只需判断某个地方是否存在一个点，由此本题有了优化空间。

这里给出一个判准：将树上所有节点表示为 \((dep,sz)\) （深度，子树大小的有序数对），若如此表示的两树结点的集合相同，则两树同构。

以下是证明：

考虑归纳。已有树 \(T_1，T_2\)，高度为 \(h\)，考虑判断两树是否同构：

若 \(h=1\)，显然成立；

若 \(h=k\) 时成立，对 \(h=k+1\)：

首先，同构是具有传递性的，因为“交换”是无序的；然后，高度为 2 的子树的叶子结点数是只取决于树根的 \(sz\) 值的，这是显然的。

由于 \(h=k\) 时同构，不妨从高层至低层地，将 \(T_1,T_2\) 前 \(k\) 层中，同子树内结点按 \(sz\) 降序从左至右排序，于是树上结点的 \(sz\) 相对位置确定。（这步相当于数学的设序，只是为了方便之后论述）

为了证明本结论，假设 \(T_1\) 已有第 \(k+1\) 层而 \(T_2\) 还只有已经证明为同构的前 \(k\) 层。现在在 \(T_2\) 第 \(k\) 层叶子结点上接入第 \(k+1\) 层的新叶子结点，对于第 \(k\) 层的某点，其在 \(T_1\) 中的 \(sz\) 确定，故以其子节点的数量确定，接上对应数量的叶子即可。随后再次按照上述方式排序，得到新树是同构于 \(T_1\) 的，故新树与排序前的 \(T_1\) 同构。

即证。

看着可能比较模糊，这里是图。考虑如此的 \(T_1\)：

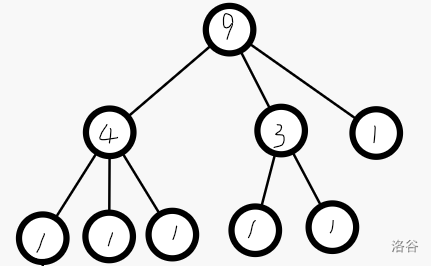
如此的 \(T_2\)：

在 \(T_2\) 的最左侧叶子加点，应加 \(4-1=3\) 个叶子，这是确定的。类似地添加其他点，最后一定可以得到同构树。

论述可能有点不严谨，于是蒟蒻用树哈希的标程（感谢@wt1551大佬）进行了 \(n=50\)，结点数为 1000 的 13000 组随机数据，结论具有一定可靠性。（或者亦可证明：对于此题，子树大小可以作为 \(\text{AHU}\) 的结点特征序）

实现

\(\text{DFS}\) 遍历序列，不建树，但是记录每个节点的深度和以他为根的子树大小，两树比较即可。

另：对于输入序列，有：一个完整子树中的 0 和 1 数量相同，且 0（或 1）的数量等于子树大小，代码还可简化，等待好心人写一个？

Code

#include <iostream>
#include <cstdio>
#include <cctype>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;

typedef long long ll;

ll n;
string s[2];
vector<pair<ll,ll> > v[2];

pair<ll,ll> dfs(int dep,int pos,int i) {
	int size=1;
	while(s[i][pos]!='1') {
		pair<ll,ll> now=dfs(dep+1,pos+1,i);
		pos=now.first;
		size+=now.second;
	}
	v[i].push_back(make_pair(dep,size));
	return make_pair(pos+1,size);
}

int main() {
	n=fr();
	while(n--) {
		v[0].clear();v[1].clear();
		cin >> s[0] >> s[1];
        s[0]+="1";s[1]+="1";
		if(s[0].length()==s[1].length()) {
			bool flag=true;
			dfs(1,0,0);
			dfs(1,0,1);
			sort(v[0].begin(),v[0].end());
		    sort(v[1].begin(),v[1].end());
		    for(register int i = 0; i < (int)v[0].size(); i++) {
				if(v[0][i]!=v[1][i]) {
					printf("different\n");
					flag=false;
					break;
				}
			}
			if(flag) printf("same\n");
		}
		else {
			printf("different\n");
		}
	}
	return 0;
}

闲话

如果觉得有用，点个赞吧！

有 hack 的话请艾特我一下！