Lecture 02 Review of Linear Algebra
图形学的依赖
基础数学
基础物理
杂项
一点美学
向量
(数学上称为向量,物理上称为矢量)
\(\vec{AB}\) = B - A
向量表示方向和长度
向量的大小\(\Vert\vec{a}\rVert\)
单位向量 \(\widehat{a} = \vec{a}/\Vert\vec{a}\rVert\),用于表示方向
向量求和
几何上
平行四边形法则、三角形法则
代数上
Cartesian Coordinates(笛卡尔坐标系)
坐标相加
在图形学中,默认向量为列向量
\[A =\begin{pmatrix}
x\\
y\\
\end{pmatrix}\\
A^T=\begin{pmatrix}
x,y\\
\end{pmatrix}\\
||A|| = \sqrt{x^2+y^2}
\]
点乘
在图形学中
向量的点乘最终结果是一个数
\[\vec{a}\cdot \vec{b} = \lVert\vec{a}\rVert \ \lVert\vec{b}\rVert \cos{\theta}\\
\cos{\theta} = {{\vec{a}\cdot \vec{b}}\over {\lVert\vec{a}\rVert \ \lVert\vec{b}\rVert}}
\]
对于单位向量
\(cos\theta = \widehat{a}\cdot\widehat{b}\)
性质
\[\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}\\
\vec{a}\cdot(\vec{b}+\vec{c}) = \vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}\\
(k\vec{a})\cdot\vec{b} = \vec{a}\cdot({k\vec{b}}) = k(\vec{a}\cdot\vec{b})
\]
在2D中
\[\vec{a}\cdot\vec{b} =
\begin{pmatrix}
x_a\\
y_a
\end{pmatrix}
\cdot
\begin{pmatrix}
x_b\\
y_b
\end{pmatrix}
= x_ax_b + y_ay_b
\]
在3D中
\[\vec{a}\cdot\vec{b} =
\begin{pmatrix}
x_a\\
y_a\\
z_a
\end{pmatrix}
\cdot
\begin{pmatrix}
x_b\\
y_b\\
z_b
\end{pmatrix}
= x_a x_b + y_a y_b + z_a z_b
\]
叉乘
-
可用于建立三维空间的直角坐标系
-
判定左和右 (如\(\vec{a}\times\vec{b}\))
叉乘结果大于0,则b在a左侧,反之在右侧(左手坐标系)
-
判断内和外(三角形光栅化的基础)
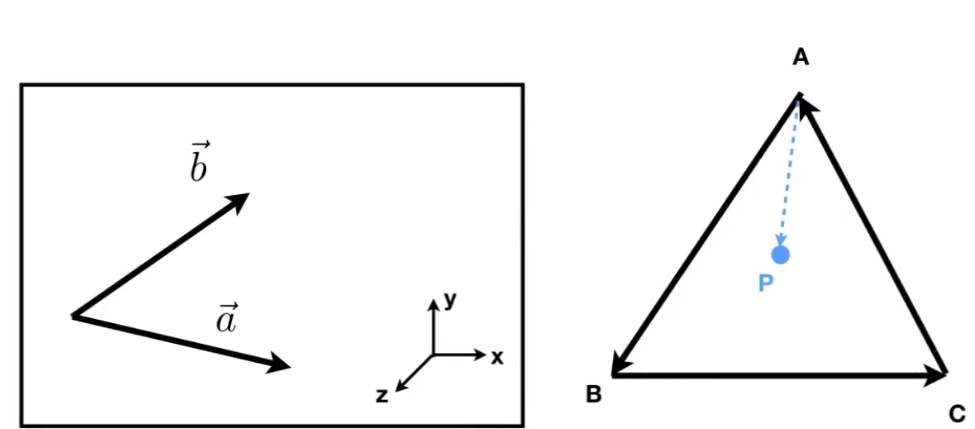
假设有A、B、C三个点逆时针排列,
\(若\vec{AB}\times\vec{AP}、\vec{BC}\times\vec{BP}和\vec{CA}\times\vec{CP}\\均判断出P在三边的同一侧(结果同号),\\说明P点在三角形内侧\\若结果为0,则自己觉得在内侧或外侧\)
![]()
向量叉乘的结果为向量,与两个原向量垂直,方向可应用右手螺旋定则,四指方向从a旋转到b,拇指方向为叉乘结果向量方向
\[a\times b = -b \times a\\
\lVert a\times b\rVert = \lVert a\rVert \lVert b\rVert sin\phi
\]
性质
\[\vec{x}\times\vec{y}=+\vec{z}\\
\vec{y}\times\vec{x}=-\vec{z}\\
\vec{y}\times\vec{z}=+\vec{x}\\
\vec{z}\times\vec{y}=-\vec{x}\\
\vec{z}\times\vec{x}=+\vec{y}\\
\vec{x}\times\vec{z}=-\vec{y}\\
\\
\vec{a}\times\vec{b} = -\vec{b}\times\vec{a}\\
\vec{a}\times\vec{a} = 0\\
\vec{a}\times(\vec{b}+\vec{c})=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}\\
\vec{a}\times(k\vec{b})=k(\vec{a}\times\vec{b})\\
\]
*若一个向量叉乘自己,得到的是长度为0的向量,而不是0
*若xy叉乘为z,则为右手坐标系,反之为左手坐标系
- OpenGL为右手坐标系(Z轴向外)
- DirextX为左手坐标系(Z轴向内)
- Vulkan为右手坐标系(Y轴向下)
- Metal为左手坐标系(Z轴向内)
- Unity和Unreal为左手坐标系(同DX)
以矩阵的形式
\[\vec{a}\times\vec{b} =
\begin{pmatrix}
y_a z_b - y_b z_a\\
z_a x_b - x_a z_b\\
x_a y_b - y_a x_b
\end{pmatrix}\\
\vec{a}\times\vec{b} = A*b =
\begin{pmatrix}
0 & -z_a & y_a\\
z_a & 0 & -x_a\\
-y_a & x_a & 0\\
\end{pmatrix}
\begin{pmatrix}
x_b\\
y_b\\
z_b
\end{pmatrix}\\
\]
矩阵
矩阵乘矩阵
\[(M\times N)(N\times P) = (M\times P)\\
左矩阵列数需等于右矩阵行数才可相乘\\
计算为前行乘后列\\
例:
\begin{pmatrix}
1 & 3\\
5 & 2\\
0 & 4
\end{pmatrix}
\begin{pmatrix}
3 & 6 & 9 & 4\\
2 & 7 & 8 & 3
\end{pmatrix}
=
\begin{pmatrix}
9 & 29& 33 & 13\\
19 & 44 & 61 & 26\\
8 & 28 & 32 & 12
\end{pmatrix}
\]
性质
-
无交换律,\(AB != BA\)
-
结合律和分配律
(AB)C = A(BC)
A(B+C) = Ab + AC
(A+B)C = AC + BC
矩阵乘向量
将向量视为列矩阵\((m\times 1)\)
\[这里将(x,y)关于y轴对称\\
\begin{pmatrix}
-1 & 0\\
0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
=
\begin{pmatrix}
-x\\
y
\end{pmatrix}
\]
别的操作
转置
转换行和列(ij->ji)
\[\begin{pmatrix}
1 & 2\\
3 & 4\\
5 & 6
\end{pmatrix}^T
=
\begin{pmatrix}
1 & 3 & 5\\
2 & 4 & 6
\end{pmatrix}
\]
性质
\((AB)^T = B^T A^T\)
单位矩阵
对角阵只有对角线上有非0的元素,单位矩阵为对角线上全是1的对角阵
\[I_{3\times 3} =
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{pmatrix}
\\
AA^{-1} = A^{-1}A = I\\
(AB)^{-1} = B^{-1}A^{-1}
\]
向量的点乘与叉乘的矩阵形式
-
点乘
\[\vec{a}\cdot\vec{b} = \vec{a^T}\vec{b}\\
=
\begin{pmatrix}
x_a & y_a & z_a\end{pmatrix}
\begin{pmatrix}
x_b\\
y_b\\
z_b
\end{pmatrix}
=(x_a x_b+y_a y_b + z_a z_b)
\]
-
叉乘
\[\vec{a}\times\vec{b} = A^*b =
\begin{pmatrix}
0 & -z_a & y_a\\
z_a & 0 & -x_a\\
-y_a & x_a & 0
\end{pmatrix}
\begin{pmatrix}
x_b\\
y_b\\
z_b
\end{pmatrix}\\
A^*为a的伴随矩阵\\
A^* =
\begin{pmatrix}
A_{11} & A_{21} & ... & A_{n1}\\
A_{12} & A_{22} & ... & A_{n2}\\
... & ... & ... & ... \\
A_{1n} & A_{2n} & ... & A_{nn}\\
\end{pmatrix}
=(A_{ij})^T
\]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号