大气渲染学习笔记

大气散射学习笔记

学习教程基于https://zhuanlan.zhihu.com/p/548799663

类型：

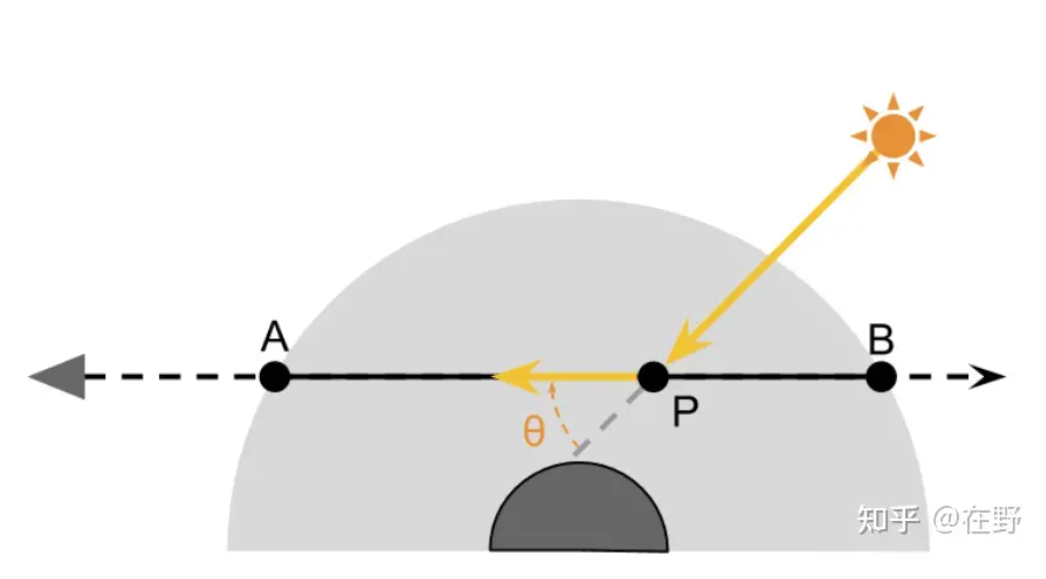
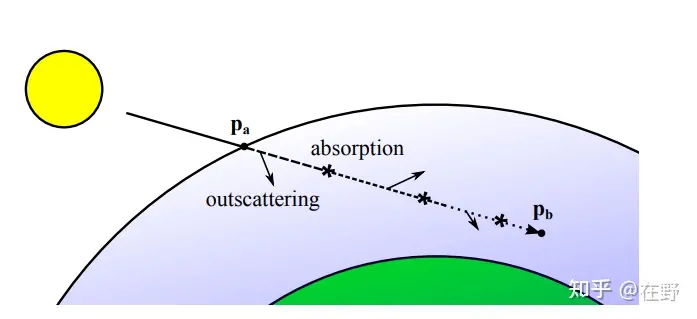
外散射：因散射导致看不到的光线

内散射：观察到本不能观察到的光线

过程:

从真空到P点：

\[透射率T_{CP} = {I_P\over I_C}\\\ 则P点光照量I_P = {I_C*T_{CP}} \]

从P点到相机：

散射函数

瑞利散射：

\[I_{PA} = I_PS(\lambda, \theta, h)T_{PA}\\\ I_{PA}计算了光从P到A点的衰减过程 \]

实际上在P到A点进行了无数个衰减,那么A点的光照实际上应该是每一个点的求和

\[在计算每一个点时，他们的光照贡献度不同，乘上一个d_s是为了让结果达到连续现象的近似结果\\\ I_A = \sum_{P∈AB} I_{PA}d_s\\\ =\sum_{P∈AB} {I_C*S(\lambda, \theta, h)*T_{CP}*T_{PA}}*d_s\\\ =I_S*\sum_{P∈AB} {S(\lambda, \theta, h)*T_{CP}*T_{PA}}*d_s \]

瑞利散射的定义

定义

\[I = I_0S(\lambda, \theta, h)\\\ S(\lambda, \theta, h) = {\pi^2(n^2-1)^2\over 2}{\rho\over N}{1\over \lambda^4}（{1+cos^2\theta}）\\\ \lambda为波长，n为粒子折射率\\\N为海平面处的大气密度，\rho(h)是高度h处的相对大气密度（相对海平面的密度）\\\ 即海平面处为1，\rho(h)随h增大而减小\\\ 将公式分解为瑞利散射系数和瑞利散射相位函数\\\ S(\lambda, \theta, h)=\beta(\lambda, h)\gamma(h) \]

\[其中\rho(h)=e^{-{h\over H}} \]

指数衰减：

设衰减系数为β

\[I_1 = I_0(1-{\beta\over 2})\\\ I_2 = I_1(1-{\beta\over 2})=I_0(1-{\beta\over 2})^2\\\ \lim\limits_{n \rightarrow\infty}(1-{\beta\over 2})^n=e^{-\beta}=exp\{-\beta\}\\\ I_P =I_S exp\{{-\beta}CP\} \]

瑞利散射是在三维空间进行的

\[\beta(\lambda, h) = \int_0^{2\pi}\int_0^{\pi}S(\lambda, \theta, h)sin\theta d\theta d\phi\\\ =\int_0^{2\pi}\int_0^{\pi} {\pi^2(n^2-1)^2\over 2}{\rho(h)\over N}{1\over \lambda^4}(1+cos^2\theta)sin\theta d\theta d\phi\\\ 提取出常数\\\ ={\pi^2(n^2-1)^2\over 2}{\rho(h)\over N}{1\over \lambda^4}\int_0^{2\pi}\int_0^{\pi}(1+cos^2\theta)sin\theta d\theta d\phi\\\ ={\pi^2(n^2-1)^2\over 2}{\rho(h)\over N}{1\over \lambda^4}{16\pi\over3}\\\ \beta(\lambda, h)={8\pi^3(n^2-1)^2\over 3}{\rho(h)\over N}{1\over \lambda^4} \]

瑞利相位函数推导：

\[\gamma(\theta)={S(\lambda, \theta, h)\over \beta(\lambda, h)}\\\ ={\pi^2(n^2-1)^2\over 2}{\rho\over N}{1\over \lambda^4}（{1+cos^2\theta}）{{3\over {8\pi^3(n^2-1)^2}}{N\over \rho(h)}\lambda^4}\\\ ={3\over 16\pi}(1+cos^2\theta)\\\ 其中\rho(h)=e^{-{h\over H}}=exp{\{-{h\over H}}\}，为密度比\\\ 当处于海平面时，h=0,\beta(\lambda) = \beta(\lambda,0)= {{8\pi^3(n^2-1)^2}\over 3}{1\over N}{1\over \lambda^4} \]

加入密度的影响

这个衰减并不完全是指数的，也会受到大气密度的影响

\[I_P = I_S exp{\{-\beta(\lambda, h_0)CQ\}}exp{\{-\beta(\lambda, h_1)QP\}}\\\ =I_Sexp{\{-(\beta(\lambda,h_0)+\beta(\lambda,h_1))d_S\}}\\\ 将长度均匀切分，乘上一个d_S达到近似的效果 \]

简化一下写法

\[I_P=I_Sexp{\{-\sum_{Q\in CP}\beta(\lambda,h_Q)d_S\}} \]

替换前文的简陋说法：

从C到P的透射率替换：

\[T(CP)=exp{\{-\sum_{Q\in CP}\beta(\lambda,h_Q)d_S\}} \]

瑞利散射中衰减因子的替换

\[T(CP)=exp{\{ {-\sum_{Q\in CP}{8\pi^3(n^2-1)^2\over 3}{\rho(h_Q)\over N}{1\over \lambda^4}d_S} \}}\\\ 分离常量\\\ T(CP)exp{\{ {-{8\pi^3(n^2-1)^2\over 3}{1\over N}{1\over \lambda^4}\sum_{Q\in CP}} \rho(h_Q)d_S\}} \]

用于求和的量称为光学深度D(cp)，这是shader里面要实际计算的东西，其余的都是乘法系数，只需计算一次

米氏散射

不会推导（

计算

散射方程

瑞利散射

瑞利散射系数定义：

\[\beta_R(\lambda)={8\pi^3{(n^2-1)^2}\over {3N_e\lambda^4}}\\ n是空气的折射率\\ N_e是海平面空气的分子密度\\ 然后\lambda是入射光的波长\\ \beta_R(\lambda,h)={8\pi^3{(n^2-1)^2}\over 3}{\rho(h)\over N}{1\over \lambda^4} \]

瑞利散射相位函数：

\[F_R(\theta)={3\over 4}(1+cos^2\theta) \]

米氏散射

米氏散射定义

（更便宜的做法）

\[\beta_M(\lambda, h)={8\pi^3(n^2-1)^2 \over 3}{\rho(h) \over N} \]

米氏散射相位函数

\[HG函数(Henyey-Greenstein):\\ \gamma_{HG}(\theta)={1\over {4\pi}}{{1-g^2}\over{1+g^2-2gcos\theta}}\\ g为控制散射几何的不对称性\\ 正值会增加向前的散射光量，负值会增加向后的散射光量 \]

密度函数

\[\rho_{R,M}(h)=exp(-{h\over H_{R,M}})=e^{-{h\over H_{R,M}}} \]

渲染解方程

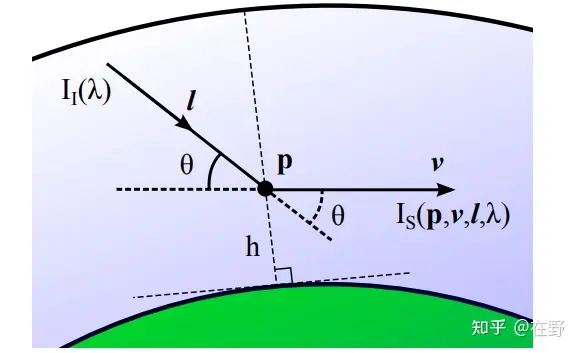
\[参数p为点，l，v为方向向量，h为p点高度，\lambda为光线波长\\ I_S的函数方程为：\\ I_S(p,v,l,\lambda)=I_I(\lambda) ( \rho_R(h)F_R(\theta){\beta_R(\lambda)\over 4\pi} \\+\\ \rho_M(h)F_M(\theta){\beta_M(\lambda)\over 4\pi} ) \]

衰减函数

\[参数意义见上图\\ T(p_a,p_b,\lambda)=exp{\{-\sum_{i\in R,M}\beta_i^e(\lambda)\int_{p_a}^{p_b}\rho_{R,M}(h(p))d_P\}}\\ \beta^e是消光系数\\ 当分子中只存在散射现象时,\beta^e_R = \beta_R \]

考虑了臭氧层对光的衰减过程（臭氧层不会散射光，只会衰减光）

在计算时只考虑臭氧层对光线的衰减

\[T(p_a,p_b,\lambda)=exp{\{-\sum_{i\in R,M,O}\beta_i^e(\lambda)\int_{p_a}^{p_b}\rho_{R,M,O}(h(p))d_P\}}\\ O是臭氧的消光系数\\ 臭氧的密度函数为： \rho O = 6e−7 ∗ \rho R \]

单散射

\[I_{S_{R,M}}^{(1)}(p_0,v,l,\lambda)\\ = I_I(\lambda)F_{R,M}(\theta){\beta_{R,M}(\lambda)\over 4\pi} \int_{p_a}^{p_b}\rho_{P,M}(h(p))T(p_c,p,\lambda)T(p,p_a,\lambda)d_P \]

考虑了散射和衰减的单散射公式

\[I_S^{(1)}=I_{S_R}^{(1)}+I_{S_M}^{(1)}\\ 将瑞利散射和米氏散射的结果相加就能得到单散射结果 \]

多重散射

嵌套多维积分可以获得高阶散射方程，但是太慢了

可以使用下面的函数来帮助实现多重散射

\[G_{R,M}^{(k)}(p,v,l,\lambda) =\int_{4\pi}F_{R,M}(\theta)I_{R,M}^{(k)}(p,\omega,l,\lambda)d_\omega \]

该函数定义了一个到达某一点p的散射k阶的光量和在方向v上的散射

k阶的聚焦函数表示聚焦在p点的光，该店的光恰好经历了k个散射事件

使用k阶函数让我们对上面的单散射函数的最终公式变形得到多重 散射最终公式:

\[I_{S_{R,M}}^{(k)}(p_0,v,l,\lambda)={\beta_{R,M}(\lambda) \over 4\pi} \int_{p_a}^{p_b}G_{R,M}^{(k-1)}(p,v,l,\lambda)\rho_{R,M}(h(p))T(p,p_a,\lambda)d_p \]

总光强就是把瑞利散射和米氏散射的结果相加，再计算k阶散射后到达观察者的所有光

需要做的就是把单次散射和更高阶散射的结果相加

\[I_S=\sum_{i=1}^{k}I_S^{(i)} \]

纹理存储

通过以下简化

1. 地球可以被看成一个完美的球形
2. 空气中的颗粒物密度只随高度变化和地理位置无关
3. 由于地球与太阳之间的距离很远，所有到达大气层的光都可以视为平行光

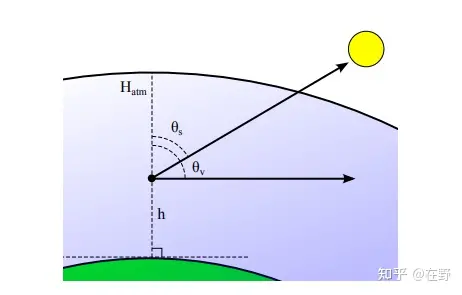
将纹理从观察者位置(XYZ)、视图方向(XYZ)、光源方向(XYZ)组成的九个维度的查找表简化到四个自由度：高度、日天顶角、视天顶角和日视方位角

其中日视方位角影响地球对大气的阴影，这种现象由于多次散射几乎看不见了，并且还会被地形遮挡，因此去除日视方位角。于是需要对瑞利散射相位函数进行调整，不然会在太阳的米氏散射上有块状阴影，解决方法是将相位函数的评估推迟到fragment shader上

纹理化

为了能在3d纹理中回去到值，需要将三个参数转化到[0,1]的范围中

\[高度h\in[0,H_{atm}], 视天顶角\theta_v\in[0,\pi], 日天顶角\theta_s\in[0,\pi]\\ \rightarrow\\ u_h\in[0,1],u_v\in[0,1],u_s\in[0,1] \]

转化函数最直接的实现是使用线性参数化，但是可以通过线性参数化方程的改变来进一步提高精度

高度重映射

大气密度随海拔高度呈现指数下降，因此在低海拔地区应该有更多地参数化集中

\[u_h=({h\over H_{atm}})^{0.5} \]

视天顶角重映射

在低海拔地区应更集中

\[u_v=\begin{cases} 0.5({{c_v-c_h}\over {1-c_h}})^{0.2}+0.5 & c_v>c_h\\ 0.5({{c_h-c_v}\over {1-c_h}})^{0.2} & c_v\quad\leqslant c_h\\ & c_h = - {\sqrt {h(2R_{Earth}+h)}\over {R_{Earth}+h}} \end{cases} \]

日天顶角重映射

虽然太阳方向在白天不会发生剧烈的变化，但是我们不需要包含低于某个阈值的太阳角度，因为夜间几乎不存在来自太阳的非散射光

\[u_s=0.5({{tan^{-1}(max(c_s,-0.1975)tan(1.26·1.1))}\over 1.1}+(1-0.26)) \]