查找

线性表的查找

顺序查找

基本思路

示例代码

#include <bits/stdc++.h>
#define LL long long
#define Pi acos(-1.0)
#define INF 2147483646
#define eps 1e-9
#define MS 100009
#define mss 17
using namespace std;
// Notice the data size
// Notice the input and output 

int p[10] = {0,1,2,3,4,5,6,7,8,9}; 

int SeqSearch(int tar){
	int i=0;
	while(i<10&&p[i]!=tar) i++; // 从头往后找 
	if(i>=10) return 0;
	else return i+1; // 找到返回逻辑序号 
}

int main() {
	int tar;
	cin >> tar;
	printf("%d\n",SeqSearch(tar));
	
	return 0;
}

二分查找

基本思路

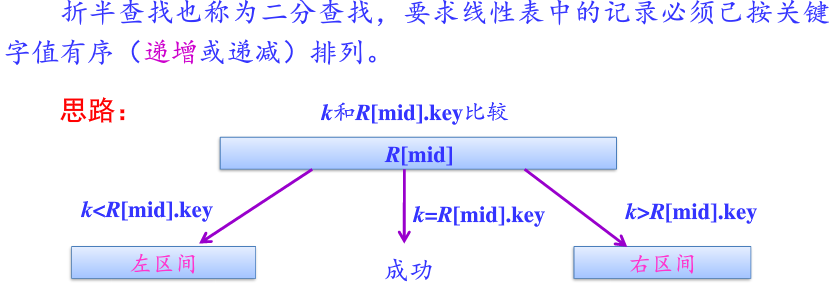
示例代码

#include <bits/stdc++.h>
#define LL long long
#define Pi acos(-1.0)
#define INF 2147483646
#define eps 1e-9
#define MS 100009
#define mss 17
using namespace std;
// Notice the data size
// Notice the input and output 

int p[10] = {0,1,2,3,4,5,6,7,8,9}; // 需要递增

int BinSearch(int tar){
	int l = 0 ,r = 9;
	while(l<=r){
		int mi = (l+r)/2;
		if(p[mi] == tar) return mi+1; // 返回逻辑序号
		if(p[mi] < tar) l = mi+1;
		else r = mi-1; 
	} 
	return 0;
}

int main() {
	int tar;
	cin >> tar;
	printf("%d\n",BinSearch(tar));
	
	
	return 0;
}

二叉排列树

插入和生成基本思路

查找基本思路

删除的基本思路

1.若删除的是叶子节点 ,则直接删除即可

2.若被删除的节点只有左子树或右子树 ,则用左子树或右子树代替

3.若删除的节点既有左子树又有右子树 ,则找到左子树的最右节点即最大节点与之替换

示例代码

#include <bits/stdc++.h>
#define LL long long
#define Pi acos(-1.0)
#define INF 2147483646
#define eps 1e-9
#define MS 10000
using namespace std;
// Notice the data size

int len;
int p[MS];

struct tnode{
	tnode *l,*r;
	int val;
}*root;

void input(){
	printf("输入元素个数：\n");
	cin >> len;
	printf("输入元素：\n");
	for(int i=0;i<len;i++) scanf("%d",&p[i]);
}

tnode *SearchBST(tnode *bt,int tar){ // 查找二叉排列树 
	if(bt==NULL||bt->val == tar) 
		return bt;
	if(bt->val > tar) 
		return SearchBST(bt->l,tar);
	else 
		return SearchBST(bt->r,tar);
}

void InsertBST(tnode *&p,int tar){ // 二叉排列树的插入 
	if(p == NULL){
		p = (tnode*)malloc(sizeof(tnode));
		p->val = tar;
		p->l = p->r = NULL;
	}
	else if(p->val > tar){
		InsertBST(p->l,tar);
	}
	else if(p->val < tar){
		InsertBST(p->r,tar);
	}
}

tnode *CreatBST(int p[],int len){ // 二叉排列树的生成 
	tnode *bt = NULL;
	for(int i=0;i<len;i++){
		InsertBST(bt,p[i]);
	}
	return bt;
}

void in(tnode *bt){ // 中序遍历 
	if(bt!=NULL){
		in(bt->l);
		printf("%d ",bt->val);
		in(bt->r);
	}
}

void Delete1(tnode *&p,tnode *&n){ // 需要删除的节点 ，该节点的左孩子 
	tnode *t;
	if(n->r != NULL) Delete1(p,n->r); // 找到最右即最大的节点 
	else{
		p->val = n->val;
		t = n;
		n = n->l;
		free(t);
	}
}

void Delete(tnode *&p){
	tnode *t;
	if(p->l == NULL){
		t = p;
		p = p->r;
		free(t);
	}
	else if(p->r == NULL){
		t = p;
		p = p->l;
		free(t);
	}
	else Delete1(p,p->l); // 左右都有孩子 
}

void DeleteBST(tnode *&p,int tar){
	if(p->val == tar) 
		Delete(p);
	else if(p->val > tar) 
		DeleteBST(p->l,tar);
	else 
		DeleteBST(p->r,tar);
}

int main() {
	input();
	// 得到二叉排列树的根节点 
	root = CreatBST(p,len);
	// 中序遍历数据为增序 
	printf("中序遍历的结果：\n");
	in(root);
	printf("\n");
	// 删除节点
	printf("输入想要删除的数据：\n");
	int tar;
	cin >> tar;
	DeleteBST(root,tar);
	printf("删除完成!\n");
	// 输出中序遍历的结果 
	printf("中序遍历的结果：\n");
	in(root);
	printf("\n");
	
	return 0;
}

平衡二叉树

我不会 ,我诚实

B树和B+树

我的心里没有B数 ,更没有B+树...

哈希表的查找

1.直接定址法: 例如学号2019001 - '张三' ,2019003 - '赵四' ,以学号减去 209000 为地址 ,h(k) = k + c;

2.除留余数法: 即模上一个素数 ,h(k) = k mod p;

3.数字分析法: 例如数据 93215 96531 53222 46333 ... 可取最后两位数字作为哈希地址 15 31 22 33

拉链法建立哈希表

基本思路

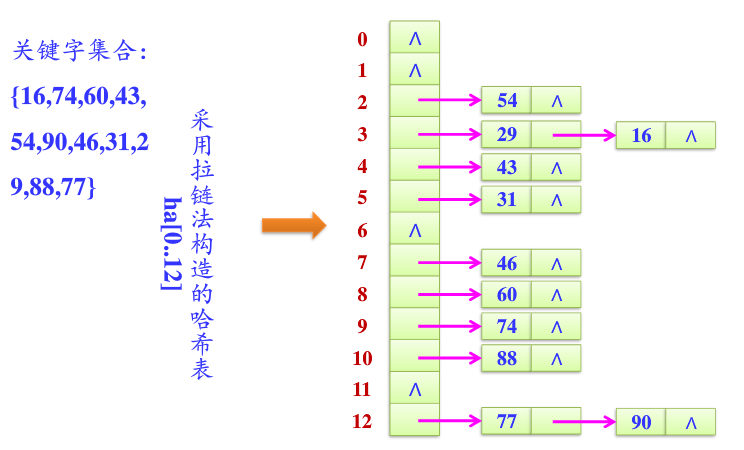
示例代码

#include <bits/stdc++.h>
#define LL long long
#define Pi acos(-1.0)
#define INF 2147483646
#define eps 1e-9
#define MS 100009
#define mss 17
using namespace std;
// Notice the data size
// Notice the input and output 

const int m = 13;

int p[15] = {16,74,60,43,54,90,46,31,29,88,77}; 
struct node{
	node *next;
	int val;
}*head[m+1],*tail[m+1];

int main() {
	// 初始化 
	for(int i=0;i<=m;i++) head[i] = tail[i] = NULL;
	// 建立 hash 表 
	for(int i=0;i<11;i++){
		int t = p[i] % m;
		node *cc = (node*)malloc(sizeof(node));
		cc->val = p[i];
		cc->next = NULL;
		if(head[t] == NULL){
			head[t] = cc;
			tail[t] = cc;
		}
		else{
			tail[t]->next = cc;
			tail[t] = tail[t]->next;
		}
	}
	// 查找 
	int tar,flag = 0;
	cin >> tar;
	node *bt = head[tar%m];
	do{
		if(bt->val == tar){
			flag = 1;
			break;
		}
		bt = bt->next;
	}while(bt!=NULL);
	// 输出结果 
	if(flag) printf("Yes\n");
	else printf("no\n");
	
	return 0;
}