Leetcode动态递归-01背包专题-刷题心得

01背包相关题目：

• 基础01背包问题：

　　问：0-1 背包问题：给定n种物品和一个容量为C的背包，物品i的重量是wi，其价值为vi 。应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

基础代码：

    for i in range(v):        #遍历所有硬币
        for j in range(c):    #遍历所有重量
            if j>=w[i]:       #如果背包可装下该硬币，则权衡装还是不装
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
            else:
                dp[i][j]=dp[i-1][j]

优化版本：

    for i in range(v):                  #遍历所有硬币
        for j in range(c,w[i]-1,-1):    #倒序遍历所有重量
            if j>=w[i]:                 #如果背包可装下该硬币，则权衡装还是不装
                dp[j]=max(dp[j],dp[j-w[i]]+v[i])

优化前空间复杂度为O（C·W），时间复杂度为O（C·W）；优化后时间复杂度不变，空间复杂度为O（C）

然而只懂得01背包远远不够，就像书上学了公式1+1=2，实际应用则是123763+276372-7388263....

下面简述leetcode4道01背包应用与变形。

• 416.分割等和子集

 

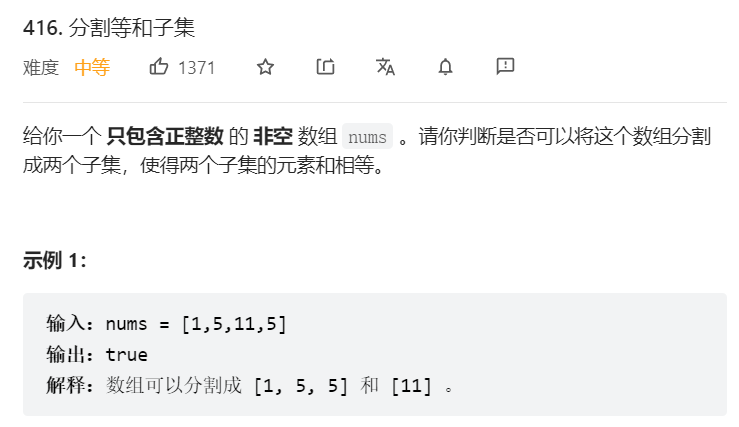
416题基本和01背包一致，nums中数组加入或不加入，使得所有加入元素之和为nums组合和的一半。则动态规划的主体部分为：

       dp = [False for i in range(int(sumNumber / 2))] 

        for i in range(len(nums)):
            for j in range(int(sumNumber / 2)-1,nums[i]-2,-1):
                if j == nums[i]-1:
                    dp[j] = True
                elif j > nums[i]-1:
                    dp[j] = dp[j] or dp[j - nums[i]]

同时可以优化：如果最大元素大于数组和的一半，则显然不能对半分割；如果数组和为奇数，则也不能对半分割

if sumNumber % 2 == 1: return False
if maxNumber > int(sumNumber / 2): return False

• 1049题最后石头重量

稍微有点绕。读题后可发现，如果每次一起粉碎的石头重量最为相近，则最后的剩余重量最小。那么于所有石头而言，将他们分割为重量最为相近的两部分即可。这就与上一题分割等和子集的分割方法一样了，只不过区别是上一题是能不能分割为等和子集，而本题是分割后两子集差为多少。

 

 

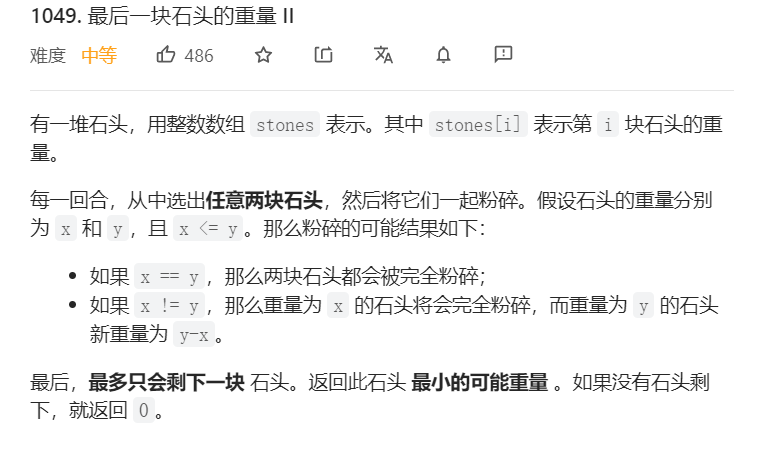
 那么动态规划的主体是一样的：

        dp=[False for i in range(half)]

        for i in range(len(stones)):
            for j in range(half-1,stones[i]-2,-1):
                if j==stones[i]-1:
                    dp[j]=True
                else:
                    dp[j]=dp[j] or dp[j-stones[i]]

最后寻找并计算差值

for i in range(half-1,-1,-1):
    if dp[i]==True:
        return sum-2*(i+1)

 

494.目标和

该题中，每个元素考虑的不是加或不加，而是赋+还是赋-。因此状态转移方程应为

dp[i][j]=dp[i-1][j-nums[i]]+dp[i-1][j+nums[i]]

此外要注意的是dp的列是所有元素组合的可能值。譬如，对于例题中的【1，1，1，1，1】而言，其组成值最大为5，最小为-5。那么本题中，我们就需要考虑到从【-5，5】这一区间的结果。

 

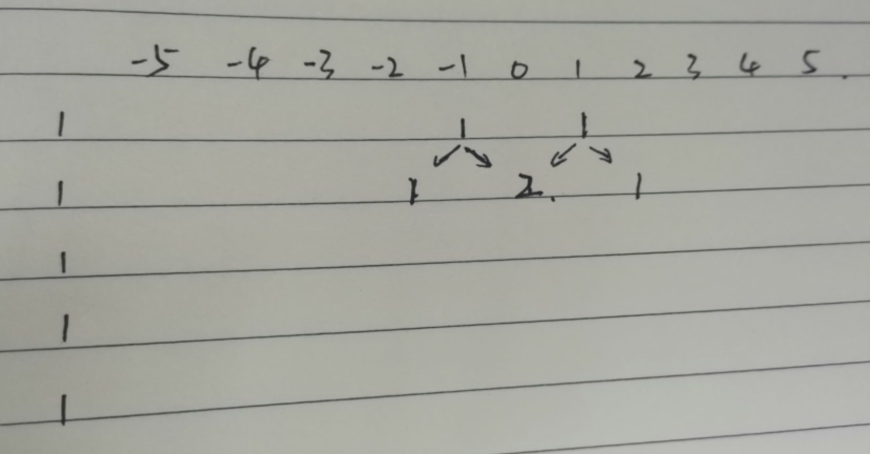
代码：

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        sum=0
        for each in nums:
            sum+=abs(each)
        if target > sum or target <-sum:return 0
        dp=[[0 for i in range(2*sum+1)]for j in range(len(nums))]

        dp[0][sum+abs(nums[0])]+=1
        dp[0][sum-abs(nums[0])]+=1

        for i in range(1,len(nums)):
            for j in range(2*sum+1):

                if j-nums[i]<0 :a=0
                else:a=dp[i-1][j-nums[i]]

                if j + nums[i] > 2 * sum: b = 0
                else:b=dp[i-1][j+nums[i]]

                dp[i][j]=a+b

        return dp[-1][sum+target]

• 474.一和零

 

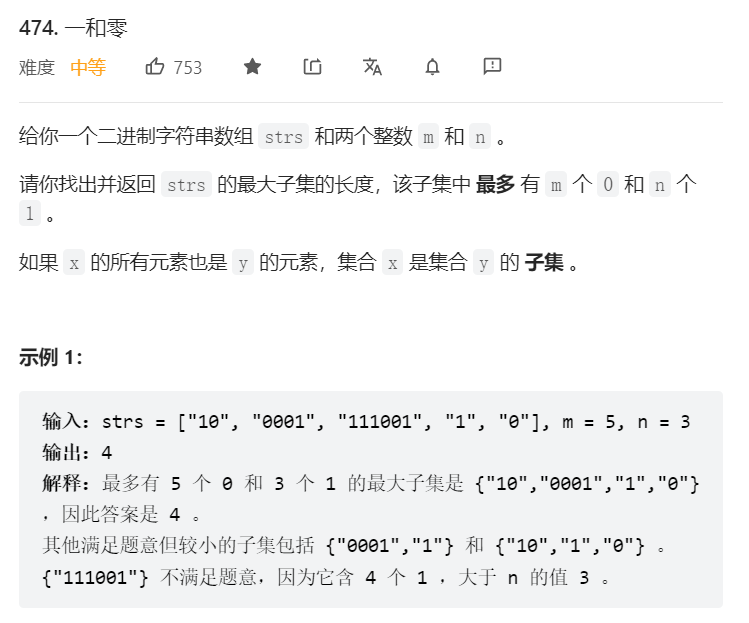
本题是二维01背包，可能因为维数增多，所以规划中心很简单：如果加上第i个字符串，符合条件且使得子集增多，则加入。

dp=[[0 for _ in range(m+1)] for _ in range(n+1)]#0|1

        for s in strs:
            m0,n1=self.count(s)
            for i in range(n,n1-1,-1):
                for j in range(m,m0-1,-1):
                    dp[i][j]=max(dp[i][j],1+dp[i-n1][j-m0])
        return dp[n][m]

    def count(self,s):
        m=0
        n=0
        for each in s:
            if each=="0":
                m+=1
            elif each=="1":
                n+=1
        return [m,n]