算法学习（持续更新）

算法学习

写在所有之前：开始准备蓝桥杯的省赛，要对过去学习的一些基础算法进行复习，在此对一些常见的算法思想和模板进行记录，这里讲的内容是基于AcWing的算法基础课理解，本人的能力有限，欢迎大家评论交流。

排序

排序是算法中常见的基础内容，许多复杂的问题都涉及到有关排序的问题。排序是一个基础问题，但不意味着它很简单，对于不同的时间复杂度、空间复杂度有要求的问题也对应着相应的解决算法，下面介绍的是集中常见且实用的排序算法。

快速排序

主要思想是分治，排序分三步走：
　　a. 确定分界点x，可以是q[ l ], q[ r ], q[ (l+r) / 2 ], 或者是随机；
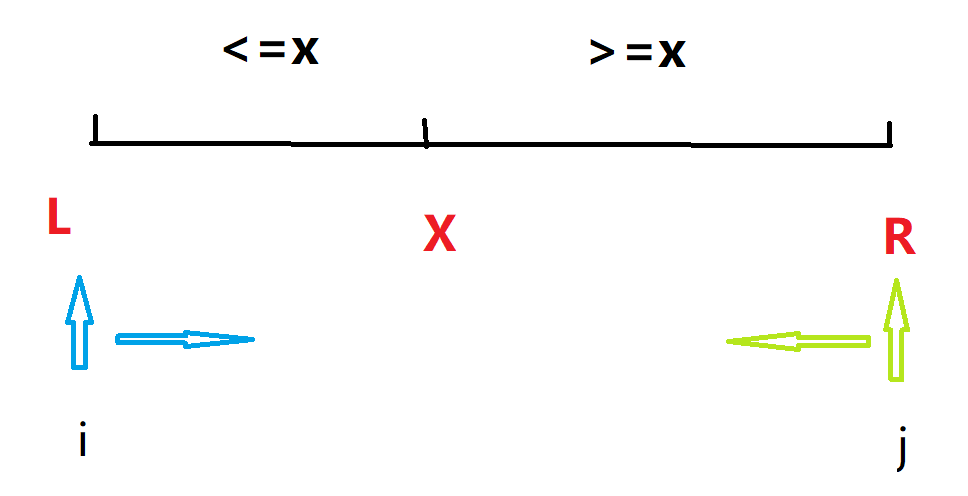
　　b. 调整区间，调整x的位置，将原区间划分为两个区间，使得x左边的区间全是小于等于x的数，x右边的区间全是大于等于x的数；【注意】x不一定在区间的中间，x可以在区间的任意位置。
　　c. 递归，处理左右两个区间。

 

模板代码

 

 

 

 

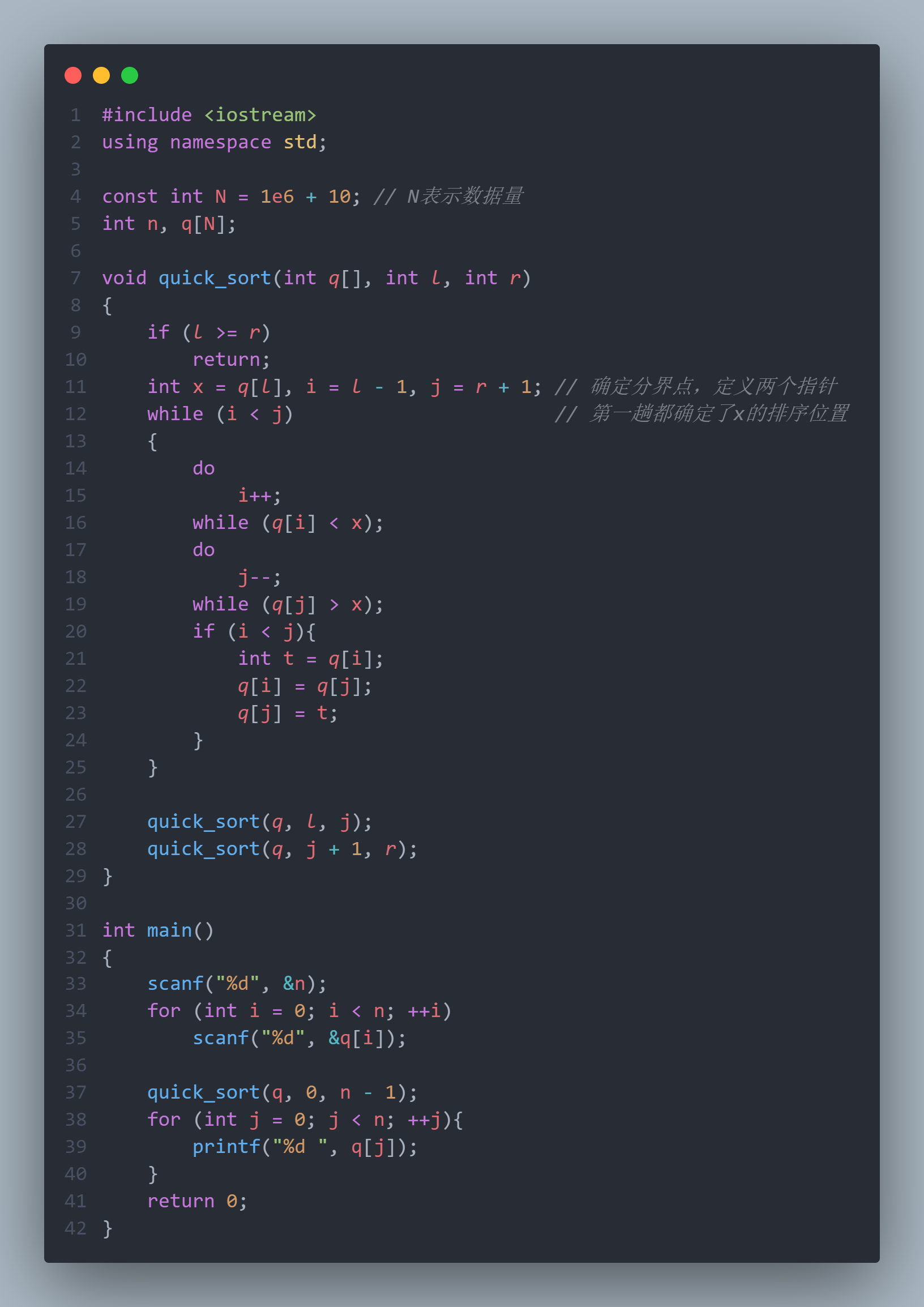
【注意】在输入大量的数据时，不要使用 cin、cout，用scanf、printf会快得多。
　　　　因为分治问题中会有很多的边界问题，这里使用的是do-while，所以所有的边界应该实际边界的两侧，这样就不会产生边界上的死循环。
　　　　当两个指针没有相遇时就接着移动（i < j），直到 x 到合适的位置。

归并排序

主要思想是分治，归并排序三步走：
　　a. 找分界点，找一个分界点，区间的中点（这里和快速排序的不一样，一个是下标，一个是数值），将区间分为left, right
　　b. 递归排序邹游两边
　　c. 归并，将左右两边合二为一（双指针算法）

代码模板

 

 

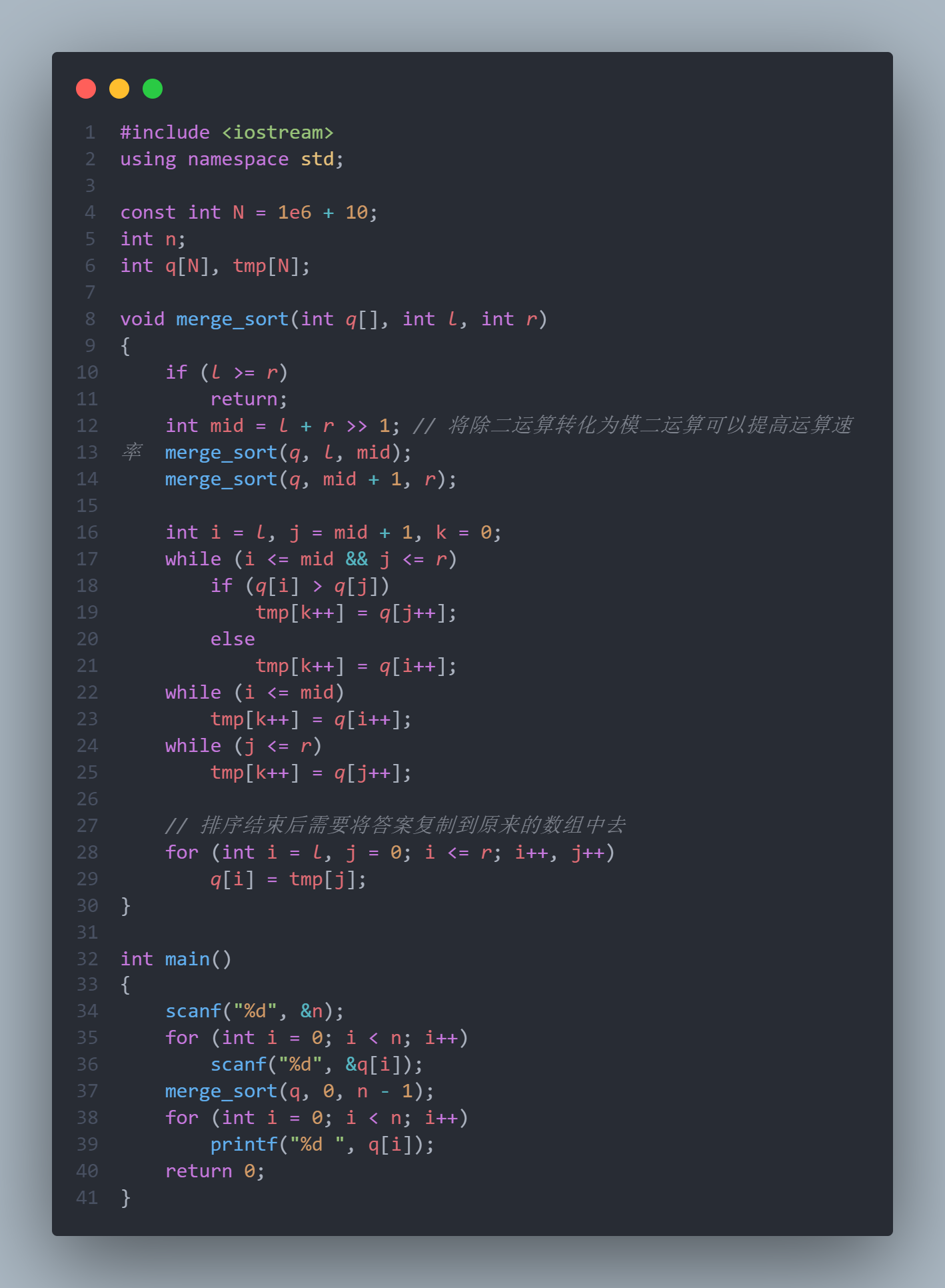
【注意】归并排序是稳定的，所谓排序稳定是指相同的数在排序前后，他们的相对位置始终不发生改变的排序。

 二分

整数二分

有单调性的题目一定可以二分（但不一定有意义），没有单调性的题目也可能可以二分。 所以二分的本质不是单调性。一种简单的描述是：将区间分为左右两部分，区间左边元素都满足某种性质，而区间右边的元素都不满足这种性质（或者恰好相反），那么我们就可以利用二分找到左区间的边界和右区间的边界。所以说单调只是其中的一种特例。

 

 

 

 

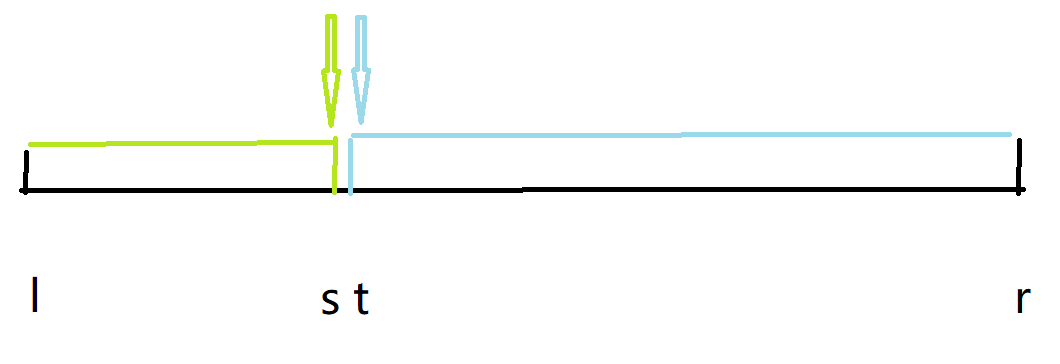
这里有两种边界情况：
　　A. 二分确定左区间的边界 s：
　　　　a. mid = (r + l + 1) / 2
　　　　b. check (mid)  ---> true: l = mid ;   ---> false: r = mid - 1;
　　　　c. 判断+递归
　　B. 二分确定右区间的边界 t：
　　　　a. mid = (r + l ) / 2
　　　　b. check (mid) ---> true: r = mid;    ---> false: l = mid + 1;
　　　　c. 判断+递归

【注意】因为 c++的整数除法是下取整，所以在寻找 s 的时候需要 +1，否则会出现mid = l 的死循环的情况。
　　　　还有一种说法是当 l = mid 时，就需要+1；当r = mid时，就不需要+1；

我们基于这道题来讲解二分算法的核心思想。这道题的解决思路就是找到s，t。分别进行两次二分。

 代码示例：

 

 

 浮点数二分

因为浮点数的除法不会出现取整问题所以就不会有边界问题，但由于浮点数是连续的，所以我们是给出一个精确度，只要一直二分到小于这个精确度就是正确的答案。

这里我们给出一个求一个浮点数的平方跟根的题目来演示。

代码示例：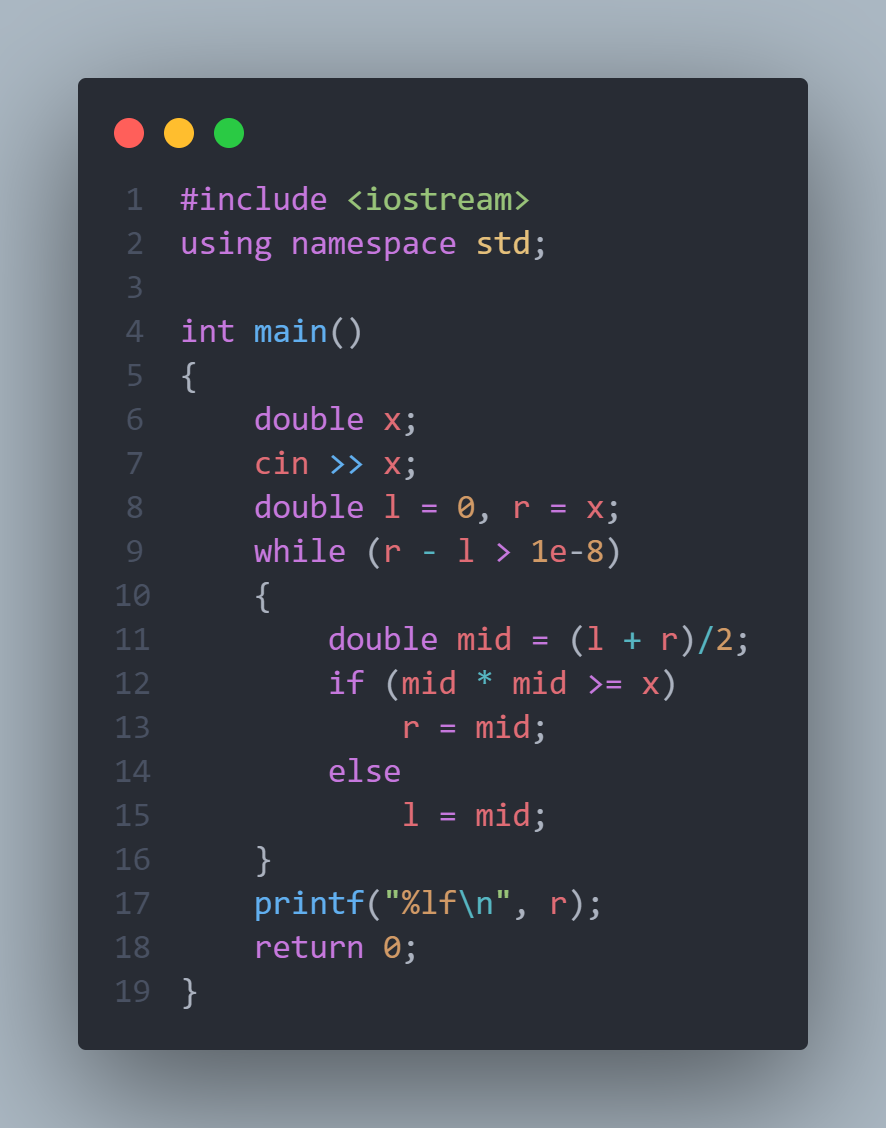
  

 高精度表示

　　在C++中，我们没有可以表示位数在1e6这么大数值的数据类型，所以我们通常会用数组来存储大整数，并且是先存低位再存高位的，这样可以方便产生最高位的进位，注意⚠️数组的每一位只存一个数位。

高精度加法：对于每一位的运算可以看作A_i + B_i + t。这里的A和B都可以是0，t是上一位的进位。
代码：

---

---