模拟退火
@
前言
最近在学习模拟退火算法,并做了一些练习题,在这里做一个总结。
一、什么是模拟退火?
1.问题描述
模拟退火适用的问题通常是一些求最优解的问题
比如,把问题抽象地看成一个长成这样的毫无规律的函数,而最优解就是函数的最低点(最高点)
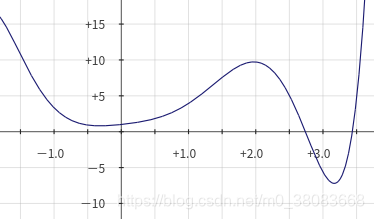
如果该函数是一个单峰(谷)函数(如二次函数),我们可以用牛顿迭代求解。而如果是如图的函数。牛顿迭代就不能保证求得最优解。
比如从A出发,可以获得局部最优解B,但这显然不是全局最优解
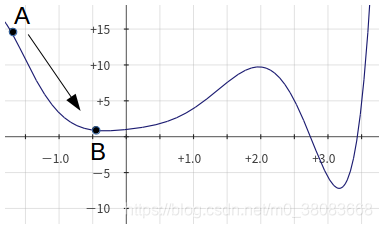
显然,牛顿迭代局限性是,过于局限在局部的一个凹部分而无法跳出去去寻找更优的解。
2.原理
为了解决这一问题,科学家们想到了物理的退火降温的过程——
一个处于很高温度的物体,现在要给它降温,使物体内能降到最低。
我们常规的思维是,越快越好,让它的温度迅速地降低。
然而,实际上,过快地降温使得物体来不及有序地收缩,难以形成结晶。而结晶态,才是物体真正内能降到最低的形态。
正确的做法,是徐徐降温,也就是退火,才能使得物体的每一个粒子都有足够的时间找到自己的最佳位置并紧密有序地排列。开始温度高的时候,粒子活跃地运动并逐渐找到一个合适的状态。在这过程中温度也会越降越低,温度低下来了,那么粒子也渐渐稳定下来,相较于以前不那么活跃了。这时候就可以慢慢形成最终稳定的结晶态了。
那么,我们可不可以把找到最优解,与形成结晶态,这两个过程联系在一起呢?
于是,模拟退火诞生了
3.算法流程
首先定义一些参数:
\(T\)——温度
\(\Delta T\) ——温度变化率,每次温度等于上一次温度乘上\(\Delta T\),实际应用时一般取\(0.95−0.99\),模拟徐徐降温
\(x\)——当前选择的解
\(\Delta x\)——解变动值
\(x_1\)——当前的目标解,等于\(x+\Delta x\)
\(\Delta f\)——当前函数值与目标函数值之差
我们给一个初始解\(x\)并让它不断变动。要模拟变动的大小随温度的降低而降低,则\(\Delta x\)应该在一个大小与\(T\)成正比的值域内随机取值。
这时候我们就要考虑是否将当前解变为目标解。分两种情况:
(1)\(f(x_1)<f(x)\),\(x=x1\)
(2)\(f(x1)>f(x),\)以\(e^{\frac{\Delta f}{T}}\)的概率接受
如此反复选择直到T趋近于0(可以设一个下限)这时候我们认为我们当前的\(x\)就是最优解
以上面那个图像寻找最优解为例
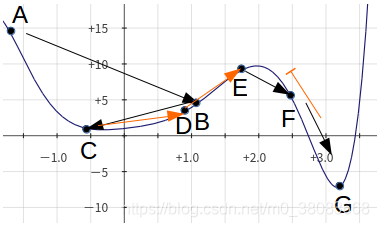
首先经过大幅波动,当前解由A->B->C,找到了一个比较满意的解。
但还不能满足。由于温度还比较大,此时接受了一些不比当前解优的目标解,C->D->E,成功地爬了上去。而温度还在慢慢减小。
终于,发现了一个更优解F,成功跳出了那个非常宽的局部凹函数
这时候,温度越来越小了,很难再次接受不比当前解优的目标解,再次翻出去。解终于渐渐趋于稳定,并最终到达了G,找到了最优解
如此看来,基于随机的模拟退火能很大程度上提高正确率,但也不可能完全正确。上面的例子只是随意模拟出的一个情况。所以要多跑几遍,取每一次得到的解的最优值。
二、例题
目前我做到的模拟退火题目大致分为两类,一类二维(平面)的问题,一类是一维(序列)的问题
1.一维
一维的模拟退火问题一般与序列的排列方式有关,每次退火我们可以改变两个位置的数值以改变排列方式。
(1)[TJOI2010]分金币
裸题
#include <bits/stdc++.h>
using namespace std;
const int Max=55;
const double D=0.99,ESP=1e-8;
int n,m,k,ans=1e9,res,tot,now,T;
int v[Max];
inline void init()
{
ans=1e9;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&v[i]);
}
inline int calc()
{
int s1=0,s2=0;
for(int i=1;i<=n/2;i++) s1+=v[i];
for(int i=n/2+1;i<=n;i++) s2+=v[i];
return abs(s1-s2);
}
inline void solve()
{
register double T=100;
int p1,p2;
now=calc();
while(T>ESP)
{
p1=rand()%n+1,p2=rand()%n+1;
if(p1==p2) continue;
swap(v[p1],v[p2]);
res=calc();
ans=min(ans,res);
if(exp(((double)now-res)/(T)) < (double)rand()/RAND_MAX) swap(v[p1],v[p2]);
else now=res;
T*=D;
}
}
int main()
{
srand(time(0));
scanf("%d",&T);
while(T--)
{
init();
if(n==1) {cout<<v[1]<<"\n";continue;}
for(int i=1;i<=50;i++)
{
random_shuffle(v+1,v+n+1);
solve();
}
printf("%d\n",ans);
}
return 0;
}
(2)Haywire
裸题
#include <bits/stdc++.h>
using namespace std;
const int Max=15;
const double D=0.99,ESP=1e-2;
int n,m,ans=1e9,res,f[Max][Max],seq[Max];
inline void init()
{
int x,y,z;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&x,&y,&z);
f[i][x]=f[x][i]=f[i][y]=f[y][i]=f[i][z]=f[z][i]=1;
seq[i]=i;
}
}
inline int calc()
{
int sum=0;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(f[i][j]) sum+=abs(seq[i]-seq[j]);
return sum;
}
inline void solve()
{
register double T=50;
int p1,p2;
while(T>ESP)
{
p1=rand()%n+1,p2=rand()%n+1;
if(p1==p2) continue;
swap(seq[p1],seq[p2]);
res=calc();
ans=min(ans,res);
if(exp((ans-res)/T) < (double)rand()/RAND_MAX) swap(seq[p1],seq[p2]);
T*=D;
}
}
int main()
{
srand(time(0));
init();
for(int i=1;i<=5;i++)
{
random_shuffle(seq+1,seq+n+1);
solve();
}
printf("%d\n",ans);
return 0;
}
(3) [HAOI2006]均分数据
对于一种序列,我们考虑贪心,将每个数放进总和最小那一组。因此,我们改变序列的排列,就能获得不同的解。因此转化成模拟退火问题
#include <bits/stdc++.h>
using namespace std;
const int Max=25;
const double D=0.99,ESP=1e-2;
int n,m;
double ans=1e9,res,aver,num[Max],sum[Max];
inline void init()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lf",&num[i]),aver+=num[i];
aver/=m;
}
inline double calc()
{
double s=0;
int id,minn;
for(int i=1;i<=m;i++) sum[i]=0;
for(int i=1;i<=n;i++)
{
minn=1e9;
for(int j=1;j<=m;j++) if(minn>sum[j]) minn=sum[j],id=j;
sum[id]+=num[i];
}
for(int i=1;i<=m;i++) s+=(aver-sum[i])*(aver-sum[i]);
return s;
}
inline void solve()
{
register double T=100;
int p1,p2;
while(T>ESP)
{
p1=rand()%n+1,p2=rand()%n+1;
if(p1==p2) continue;
swap(num[p1],num[p2]);
res=calc();
ans=min(ans,res);
if(exp((ans-res)/T) < (double)rand()/RAND_MAX) swap(num[p1],num[p2]);
T*=D;
}
}
int main()
{
srand(time(0));
init();
for(int i=1;i<=2;i++)
{
random_shuffle(num+1,num+n+1);
solve();
}
printf("%.2f\n",sqrt(ans/m));
return 0;
}
(4)[SCOI2008]城堡
将没有城堡的城市排成一排,每次改变顺序后取前\(k\)个城市修建城堡
#include <bits/stdc++.h>
using namespace std;
const int Max=55;
const double D=0.99,ESP=1e-16;
int n,m,k,ans=1e9,res,tot,now;
int f[Max][Max],seq[Max],r[Max],d[Max],tag[Max];
inline void init()
{
int x;
memset(f,0x3f,sizeof(f));
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++) scanf("%d",&r[i]);
for(int i=1;i<=n;i++) scanf("%d",&d[i]),f[i][i]=0;
for(int i=1;i<=m;i++) scanf("%d",&x),tag[x+1]=1;
for(int i=1;i<=n;i++) f[r[i]+1][i]=f[i][r[i]+1]=min(d[i],f[r[i]+1][i]);
}
inline void pre()
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
for(int i=1;i<=n;i++) if(!tag[i]) seq[++tot]=i;
}
inline int calc()
{
int minn,maxx=0;
for(int i=1;i<=k;i++) tag[seq[i]]=1;
for(register int i=1;i<=n;i++)
{
if(tag[i]) continue;
minn=1e9;
for(register int j=1;j<=n;j++)
if(tag[j]) minn=min(minn,f[i][j]);
maxx=max(maxx,minn);
}
for(int i=1;i<=k;i++) tag[seq[i]]=0;
return maxx;
}
inline void solve()
{
register double T=50;
int p1,p2;
now=calc();
while(T>ESP)
{
p1=rand()%n+1,p2=rand()%n+1;
if(p1==p2) continue;
swap(seq[p1],seq[p2]);
res=calc();
ans=min(ans,res);
if(exp(((double)now-res)/(T*2)) < (double)rand()/RAND_MAX) swap(seq[p1],seq[p2]);
else now=res;
T*=D;
}
}
int main()
{
srand(time(0));
init();
pre();
for(int i=1;i<=2;i++)
{
random_shuffle(seq+1,seq+tot+1);
solve();
}
printf("%d\n",ans);
return 0;
}
2.二维
二维的模拟退火问题一般与坐标有关,每次更新坐标得到新的函数值。
(1)[JSOI2004]平衡点 / 吊打XXX
平衡状态势能最小,即留在桌面上的绳尽量短,也就是最小化\(\sum G*d_i\)(\(d_i\)为\(i\)点到该点的距离)
#include <bits/stdc++.h>
#define RD T*(rand()*2-RAND_MAX)
using namespace std;
const int Max=1005;
const double EPS=1e-14,D=0.97;
int n,m;
double ans,best,res,bx,by,x_0,y_0,x_1,y_1;
double x[Max],y[Max],w[Max];
inline double calc(double xx,double yy)
{
double sum=0,dx,dy;
for(int i=1;i<=n;i++)
{
dx=x[i]-xx,dy=y[i]-yy;
sum+=sqrt(dx*dx+dy*dy)*w[i];
}
return sum;
}
inline void init()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf",&x[i],&y[i],&w[i]);
bx+=x[i],by+=y[i];
}
ans=best=calc(bx/=n,by/=n);
}
inline void solve()
{
srand(time(0));
m=1;
while(m--)
{
ans=best,x_0=bx,y_0=by;
for(register double T=100000;T>EPS;T*=D)
{
x_1=x_0+RD,y_1=y_0+RD;
res=calc(x_1,y_1);
if(best>res) best=res,bx=x_1,by=y_1;
if(ans>res || exp((ans-res)/T) > (double)rand()/RAND_MAX) x_0=x_1,y_0=y_1,ans=res;
}
}
printf("%.3f %.3f",bx,by);
}
int main()
{
init();
solve();
return 0;
}
(2)Run Away
裸题
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <ctime>
#include <cmath>
#define RD T*(rand()*2-RAND_MAX)
using namespace std;
const int Max=1005;
const double D=0.98,ESP=1e-6;
int n,m,k,T;
double x[Max],y[Max],now,res,ans,fx,fy,px,py,nx,ny;
inline void init()
{
ans=0.0;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;i++) scanf("%lf%lf",&x[i],&y[i]);
px=n/2.0,py=m/2.0;
}
inline void modify(double &x,double &y)
{
x=min(x,(double)n),x=max(x,0.0);
y=min(y,(double)m),y=max(y,0.0);
}
inline double dis(double a,double b,double c,double d)
{
return sqrt((a-c)*(a-c)+(b-d)*(b-d));
}
inline double calc(double xx,double yy)
{
double len=1e9;
for(int i=1;i<=k;i++) len=min(len,dis(xx,yy,x[i],y[i]));
return len;
}
inline void solve()
{
register double T=50;
now=calc(px,py);
while(T>ESP)
{
nx=px+RD;ny=py+RD;
modify(nx,ny);
res=calc(nx,ny);
if(ans<res) ans=res,fx=nx,fy=ny;
if(now<res || exp(((double)res-now)/T) > (double)rand()/RAND_MAX) now=res,px=nx,py=ny;
T*=D;
}
}
int main()
{
srand(time(0));
scanf("%d",&T);
while(T--)
{
init();
for(int i=1;i<=5;i++) solve();
printf("The safest point is (%.1f, %.1f).\n",fx,fy);
}
return 0;
}
(3)A Star not a Tree?
裸题
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <ctime>
#include <cmath>
#define RD T*(rand()*2-RAND_MAX)
using namespace std;
const int Max=105;
const double D=0.98,ESP=1e-6;
int n;
double x[Max],y[Max],now,res,ans=1e9,px,py,nx,ny;
inline void init()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]),px+=x[i],py+=y[i];
px/=n,py/=n;
}
inline double dis(double a,double b,double c,double d)
{
return sqrt((a-c)*(a-c)+(b-d)*(b-d));
}
inline double calc(double xx,double yy)
{
double len=0;
for(int i=1;i<=n;i++) len+=dis(xx,yy,x[i],y[i]);
return len;
}
inline void solve()
{
register double T=20;
now=calc(px,py);
while(T>ESP)
{
nx=px+RD;ny=py+RD;
res=calc(nx,ny);
if(ans>res) ans=res;
if(now>res || exp(((double)now-res)/T) > (double)rand()/RAND_MAX) now=res,px=nx,py=ny;
T*=D;
}
}
int main()
{
srand(time(0));
init();
for(int i=1;i<=1;i++) solve();
printf("%.0f\n",ans);
return 0;
}
(4)[JSOI2016]炸弹攻击1
对于每个点,得到距离该点最近的建筑边界,然后寻找这个范围内的敌人数量。
#include <bits/stdc++.h>
using namespace std;
const int Max=1005;
int n,m;
double R,x[105],y[105],r[105],p[Max],q[Max];
inline void init()
{
scanf("%d%d%lf",&n,&m,&R);
for(int i=1;i<=n;i++) scanf("%lf%lf%lf",&x[i],&y[i],&r[i]);
for(int i=1;i<=m;i++) scanf("%lf%lf",&p[i],&q[i]);
}
inline double rand01()
{
return rand() % 10001 / 10000.;
}
inline void randPos(double &x_0,double &y_0)
{
x_0 = 2 * R * rand01() - R;
y_0 = 2 * R * rand01() - R;
}
inline double sqr(double x)
{
return x * x;
}
inline double dis(double ax, double ay, double bx, double by)
{
return sqrt(sqr(ax - bx) + sqr(ay - by));
}
inline int calc(double a, double b)
{
double res = R;
for (int i = 1; i <= n; i++) {
res = min(res, dis(a, b, x[i], y[i]) - r[i]);
}
if (res < 0) return 0;
int ans = 0;
for (int i = 1; i <= m; i++) {
ans += dis(a, b, p[i], q[i]) <= res;
}
return ans;
}
inline void solve()
{
double x_0,y_0;
int ans=0;
for(int tim=1;tim<=20;tim++)
{
randPos(x_0,y_0);
double T = R;
int res, cur = calc(x_0, y_0);
while (T > 1e-2) {
double x_1 = x_0 + 2 * T * rand01() - T;
double y_1 = y_0 + 2 * T * rand01() - T;
res = calc(x_1, y_1);
if (res > cur || exp(10000 * (res - cur) / T) > rand01()) {
cur = res;
x_0 = x_1, y_0 = y_1;
}
ans = max(ans, cur);
T-=T/500;
}
}
cout<<ans;
}
int main()
{
srand(time(0));
init();
solve();
return 0;
}
总结
1.关于参数
\(T,\Delta T\)先调大一点,下限精度调高一点,先保证正确率再调整
2.最大最小值区别
求最小值
if(now>res || exp(((double)now-res)/T) > (double)rand()/RAND_MAX)
求最大值
if(now<res || exp(((double)res-now)/T) > (double)rand()/RAND_MAX)
3.二维边界
有些二维题目有边界要求,注意得到的新坐标要调整到边界内


 浙公网安备 33010602011771号
浙公网安备 33010602011771号